§6. Модель Клейна геометрии Лобачевского (доказательство непротиворечивости л)

Рассмотрим на евклидовой плоскости некоторую окружность с центромOи радиусомr=1. Назовем ееабсолютом.- круг с границей, а-множество внутренних точек этого круга. Вот на этом объекте и будет построена модель.

- точкой назовем любую евклидову точку М.

- прямой – любую хорду без концов окружности . Отношения инцидентности и лежать между в обычном смысле.

Ясно, что аксиомы игрупп Гильберта (для плоскости) имеют место. А значит, имеют место и следствия из них и можно ввести соответствующие понятия: луча (полухорды), полуплоскость (открытый сегмент), флаг, угол и т.д.

А вот с группой несколько сложнее. Для этого необходимо, ввести понятие конгруэнтности (равенства). Введем преобразования, которые круг отображают на себя. На самом деле это будут преобразования стационарной подгруппы круга группы проективных преобразований плоскости. Т.е. модель, которую мы строим, вообще говоря, является проективной моделью, если окружность рассматривать как овальную линию на проективной плоскости (на расширений евклидовой плоскости).

Напомнимсложным отношением четырех точек прямой А, В, С иDназывается число (АВ, СD)=

Свойства: 1⁰. Если (АВ, СD)=(АВ, СD^/), тоD=D^/

2⁰. (АВ, СD)=(СD, АВ)=(ВА,DС)=(DС, ВА)

3⁰. Если четыре точки прямой заданы своими координатами М₁(х₁,у₁), М₂(х₂,у₂), М₃(х₃,у₃), М₄(х₄,у₄), то (М₁М₂,М₃М₄)=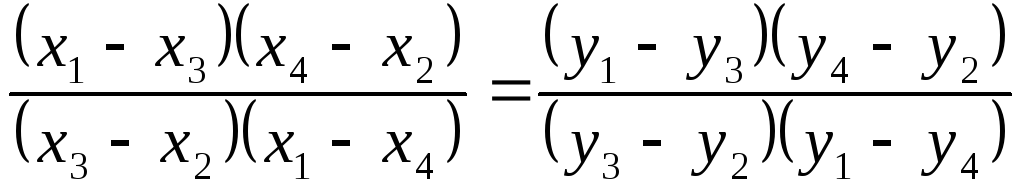

Опр. 1Биективное отображением f: назовем - преобразованием, если

а) внутренние точки круга  переходят во внутренние точки того же круга, а граничные – в граничные

б) Любая хорда окружности  переходит в некоторую хорду этой же окружности и при этом сохраняется сложное отношение соответственных точек.

Корректность.Множество таких преобразований не пусто, т.к. евклидовы повороты вокруг т. О и евклидовы симметрии относительно диаметров, удовлетворяют всем требованиям, поскольку сохраняется простое отношение трех, а значит и сложное отношение четырех точек прямой.

Но ими множество -преобразований не исчерпывается, если бы исчерп., то о Лобачевском и речи бы не было. Рассмотрим следующие отображенияf:в системе координатOху :

(1)

(2)

Каждая точка множества имеет образ, т.к. 1-ах0 и т.к. -1х1 проверим а)1-х^/2-у^/2=, ясно, если правая часть0, то и левая0, если правая часть =0, то и лева часть=0.

Далее из вида формул (2) заключаем, что то же самое имеет место и для прообразов f:биективно и удовлетворяют условие а).

Отображение f - инволютивно, т.к. М^/=f(M),f(M^/)=Mf^-1=f. Непосредственной подстановкой формул (2) в уравнение прямой Ах+Ву+С=0 убеждаемся в выполнении первой части свойства б). Чтобы убедится в том, что сохраняется сложное отношение четырех точек достаточно подставить формулу (2) в свойство 3⁰сложного отношения (). Возможно, есть и другие- преобразования (не все они инволютивны). Для доказательства аксиомIIIгруппы нам понадобятся свойства этих- преобразований.

1. Еслиfиg- преобразования, тоfgиf^-1являются- преобразованиями.

2. Любое- преобразование сохраняет отношение «лежать между» точек круга.

Доказательство.Пусть А, В, Си А-В-С. А^/, В^/, С^/- образы. А,В,Сuv, А^/,В^/,С^/u^/v^/: если А и С концы хорды, то утверждение очевидно. Пусть точкаuне совпадает ни с А, ни с С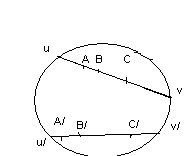. Тогда (АС,ВU)=(А^/С^/,В^/U^/), т. е.(АС,U)<0, и т.к. границав границу, то (А^/С^/,U^/)<0, но (AC,B)>0(А^/С^/, В^/)>0B^/лежит между А^/и С^/. ч.т.д.

3.При- преобразовании отрезок, принадлежащий кругу, переходит в отрезок, полухорда в полухорду, сегмент в сегмент, а если ввести понятие-флага, то-флаг-флаг. ( т.к. полупл.в полупл.)

4.Какова бы ни была точка А круга, существует инволютивное-преобразование, которое переводит точку А в центр О круга, а точку О в точку А.

Доказательство: Пусть ОА=а(<1) систему координат Оху выберем так, чтобы А имела координаты (а, 0) тогда- преобразование, заданное формулами (1)-искомое. Ч.т.д.

5.Каковы бы ни были флагии- преобразование, котороеI₁переводит вI₂.

Доказательство:f₁(A₁) = О, f₂(A₂) = О,f₀- вращение с отражениями:f₁(I₁)=I₁^/, f₂(I₂)=I₂^/f₂ f₀ f₁- искомое.

6. Каковы бы ни были полухорды А₁U₁и А₂U₂, существует- преобразование, которое полухорду А₁U₁переводит в полухорду А₂U₂.

7. Если-преобразование какой-нибудь- флаг переводит в себя, то оно является тождественным преобразованием.

Теперь введем отношение конгруэнтности (равенства).

Отрезок АВ называется конгруэнтным (равным) отрезку А^/В^/, если  такое - преобразование, которое отрезок АВ переводит в отрезок А^/В^/.Угол hk считается равным h^/k^/ , если  - преобразование f, которое угол hk переводит в h^/k^/ (т.е. h^/=f(h) и k^/=f(k) или k^/=f(h) и h^/=f(k)).

Замечание.Всегда можно считать, чтоh^/=f(h) иk^/=f(k), т.к. иначе по свойству4 переведем его в угол с вершиной О и добавим симметрию с осью, совпадающей с биссектрисой.

Теперь мы готовы к доказательству H_III. Докажем выполнениеIII₁, III₂,III₃.

III₁. Пусть АВ данный отрезок на лучеh, аh^/- луч, исходящий из т.А^/. Докажем, чтоВ^/h^/,такая что А^/В^/=АВ. По6, существует- преобразованиеf: АUА^/U^/. Тогдаh^/=f(h) и В^/=f(В)h^/ - искомая точка и поdfА^/В^/=АВ.

Замечание:В^/- единственна, самостоятельно.

III₂Если АВ=А^/В^/и АВ= А^//В^//, то А^/В^/= А^//В^//. Очевидно из1.

III₃А-В-С, А^/-В^/-С^/, если АВ=А^/В^/и ВС=В^/С^/, то АС=А^/С^/. По6- преобразованиеf: ВVB^/V^/, и т.к. хордахорду, то ВUB^/V^/ . Пусть А₁=f(А), С₁=f(С) т.к. ВА=B^/A^/ и ВА=B^/А₁А₁=А^/, аналогично С₁=С^/f: АСА^/С^/, т.е. АС= А^/С^/.

III₄. Пусть дан уголhkи флаг (А^/,h^/,^/). Докажем, что существует единственный лучk^/^/, так чтоhk=h^/k^/. Рассмотрим- флагиI=(АU,) иI^/=(А^/U^/,^/) по свойству 5- преобразованиеf:I^/=f(I). Лучk^/=f(k)-искомыйhk=h^/k^/.

Единственность.Пустьk^//– луч, т. чтоhk=h^/k^//иk^// I^/, тогдаh^/k^/=h^/k^//-преобразованиеg:h^/=g(k^/),k^//=g(k^/)- преобразованиеg-флагI^/переводит в себя, значит оно тождественноеk^/иk^//-совпадают.

III₅. Пусть вАВС и А^/В^/С^/АВ=А^/В^/, АС=А^/C^/иВАС=В^/А^/С^/. Докажем, что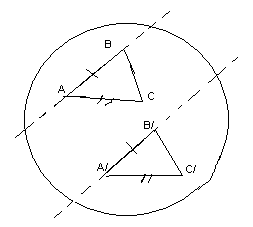АВС=А^/В^/С^/.

H_IVимеет место, т.к. она эквивалентнаThДедекинда.

V^*тоже (см. картинку).

Значит, мы построили модель геометрии Лобачевского. Тем самым, доказав, что _лнепротиворечива, если непротиворечива_Н, но_Ннепротиворечива, если непротиворечива арифметика действительных чисел.

Теорема 1._Л непротиворечива, если непротиворечива арифметика действительных чисел.

Теорема 2.V постулат не зависит от остальных четырех групп аксиом Гильберта евклидовой планиметрии.