§4. Взаимное расположение двух прямых на плоскости Лобачевского

Сначала перечислим некоторые свойства // прямых:

Свойство 1.Если АВ//СD, то существует ось симметрии прямых АВ и СD.

Свойство 2.Если АВ//СD, то СD//АВ.

Свойство 3.Если АВ//ЕF, ЕF//СDи прямые АВ и СDне совпадают, то АВ//СD. (самостоятельно).

Доказательство свойства 1.h-биссектрисаQРВ,h-биссектрисаРQD.hпересекаетQDв т. Еkпересекаетhв т.S.SН₁=SН₂=SН₃Sравноудалена от АВ и СD.d– биссектрисаН₁SН₂.S_d: АВСD.

Доказательство свойства 2АВ//СDd-ось симметрий. РАВ произвольная точка. ПриS_d: РQСD. Достаточно доказать, что любой внутренний лучРQDпересекает АВ. Пустьh^/-внутренний лучРQD,h- симметричный ему лучQРВ. Т.к.hпересекает, СDh^/пересекает АВ.

Опр. 1 Две ненаправленные прямые а и в будем называть параллельными, если на этих прямых можно выбрать направления так, чтобы они были параллельны в смысле Опр.1§2.

Опр. 2Две прямые на плоскости Лобачевского называются расходящимся (или сверхпараллельными), если они не пересекаются и не параллельны.

Очевидно, что через каждую точку М, не лежащую на прямой а, проходит бесконечное множество прямых, каждая из которых расходится с прямойа.

Вывод:На плоскости Лобачевского в отличие от Евклидовой плоскости имеются три случая взаимного расположения двух прямых: пересекаются, параллельны или расходятся.

В качестве примера свойства расходящихся прямых приведем следующее:

Теорема 1. Две прямые, имеющие общий перпендикуляр, расходятся.

Доказательство: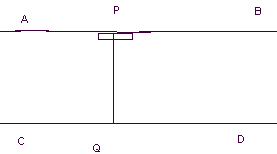Пусть АВ и СDданные прямые, а РQих общий. АВ и СDне пересекаются. Значит либо расходится, либо //, но углыQРВ иQРА - углы параллельности, а они должны быть острыми. Значит АВ и СD- расходятся.

Следствие. На плоскости Лобачевского не существует общего перпендикуляра двух параллельных прямых.

Теорема 2.Две различные прямые на плоскости Лобачевского не могут иметь более, чем один общий перпендикуляр.

Доказательство: 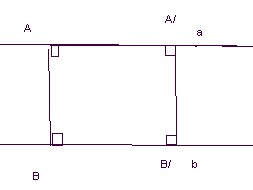_АА/В/В=4d, а должно быть<4d.

Замечание . Позже мы докажем и теорему существования:любые две расходящиеся прямые имеют общий перпендикуляр.

Теорема 3.Пусть лучи РР^/иQQ^/лежат в одной полуплоскости с границей РQ,РQQ^/- прямой, аQРР^/- прямой или тупой. Тогда если М переменная точка луча РР^/, а Н- проекция этой точки на прямуюQQ^/, то функция МН=f(МР), является монотонной, неограниченно возрастающей функцией (без доказательства).

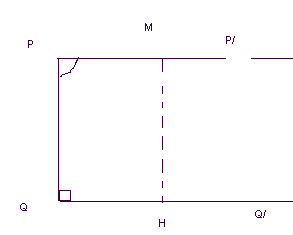
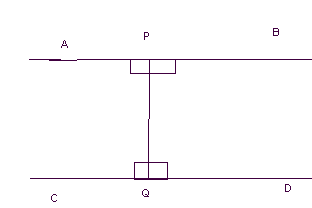
Обсудим ситуацию: что происходит с точками расходящихся прямых?

Пусть АВ и СD- расходящиеся прямые, по замечанию к Тh1, существуетPQ- их общий, который является осью симметрии. Тогда по теореме 3, т. М удаляется от СDкак в одном, так и в другом направлении. Т.е. расходящиеся прямые неограниченно «расходятся».

Пусть прямые АВ//СDи РQСD. Если М удаляется в сторону противоположную направлению параллельности, то расстояние от нее доCDнеограниченно возрастает. А если М удаляется в сторону //, то это расстояние0. Т.е. они как бы сходятся (ясно, что асимптотически).

В связи только что изложенным фактом на плоскости Лобачевского можно рассмотреть три типа пучков.

1. Пучок пересекающихся прямых : множество всех прямых, проходящих через одну точку.

2. Пучок // прямых: множество, состоящие из направленной прямой и всех направленных прямых, параллельных ей.

3. Пучок расходящихся прямых: множество всех прямых плоскости перпендикулярных данной прямой (в «малом» они все себя ведут так, как мы нарисовали).