
книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2
.pdf
|
|
|
|
|
Глава 9. Расчет переходных процессов классическим методом |
73 |
||||
условие |1 Χ h|9 1 не может быть достигнуто ни при каком значении h > 0, ò. å. |
||||||||||
устойчивому решению дифференциального уравнения (***) не соответствует ка- |
||||||||||
кое-либо устойчивое решение разностного уравнения явного |
|
|
|
|
||||||
метода Эйлера. Поэтому явный метод Эйлера по условиям ус- |
|
|
|
|
||||||
тойчивости непригоден для интегрирования устойчивых урав- |
|
|
|
|
||||||
нений состояния вида (*), собственные значения матриц кото- |
|
|
|
|
||||||
рых могут иметь нулевые вещественные части. В этом случае |
|
|
|
|
||||||
на каждом отдельном шаге интегрирования может быть до- |
|
|
|
|
||||||
стигнута вполне приемлемая точность, в то время как аппрок- |
|
|
|
|
||||||
симирующая эти значения функция не соответствует функции |
Ðèñ. 9.33 |
|
||||||||
истинного решения исходного дифференциального уравнения. |
|
|
|
|
||||||
Рассмотрим случай, когда Re Χ < 0 и метод Эйлера может быть применен |
||||||||||
по условию устойчивости. Условие |1 Χ h|9 1накладывает жесткие ограничения |
||||||||||
на шаг. Например, при чисто вещественном значении Χ < 0 из этого условия |
||||||||||
вытекает следующее ограничение на максимально допустимый шаг дискретиза- |
||||||||||
öèè: h < Ε2/ΧΕ. |
|
|
|
|
|
|
|
|||
Таким образом, при интегрировании явным методом Эйлера уравнений со- |
||||||||||
стояния (*) с большими по модулю собственными значениями матриц коэффи- |
||||||||||
циентов шаг интегрирования по условиям устойчивости должен быть выбран |
||||||||||
достаточно малым. Такая ситуация возникает, например, при обработке уравне- |
||||||||||
ний электрических цепей с малыми постоянными времени, что соответствует |
||||||||||
большим по модулю вещественным частям собственных значений матриц урав- |
||||||||||
нений состояния. При этом попытка увеличить шаг более величины, определяе- |
||||||||||
мой его максимальной оценкой, приводит к резкому возрастанию погрешности |
||||||||||
(«взрыву» погрешности) и нарушению адекватности вычисленных значений ис- |
||||||||||
тинному решению дифференциального уравнения. |
|
|
|
|
||||||
Применим для решения уравнения (**) разностное уравнение неявного мето- |
||||||||||
да Эйлера |
|
xn 1 xn hΧxn 1 èëè xn 1 (1 hΧ) 1 xn . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Для этого разностного уравнения решение также можно найти в виде x |
n |
n . |
||||||||
|
|
|
|
n + hΧΔ0 |
|
|
|
|
0 |
|
Тогда |
0 |
n+1 |
0 |
n+1, (1 – Χh) 1 èëè |
(1 – Χh)–n и, следовательно, |
|||||
xn x0 (1 |
Χh) n . Это выражение является приближенным представлением точ- |
|||||||||
ного решения |
|
|
|
|
|
|
|
|
||
x(t |
n |
) x(nh) x |
n |
x |
0 |
enΧh x |
0 |
(e n )Χh x |
0 |
(e(Χh) ) n x |
0 |
(1 Χh) n . |
|
|
|
|
|
|
|
||||||
Для обеспечения асимптотической устойчивости послед- |
|
|
||||||||||
него уравнения необходимо, чтобы Ε(1 – h Χ)–1Ε< 1 èëè äëÿ |
|
|
||||||||||
Χ + j (1 – h )2 + (h )2 > 1. Областью устойчивости |
|
|
||||||||||
данного метода является вся плоскость, за исключением еди- |
|
|
||||||||||
ничного круга в правой полуплоскости с центром в точке |
|
|
||||||||||
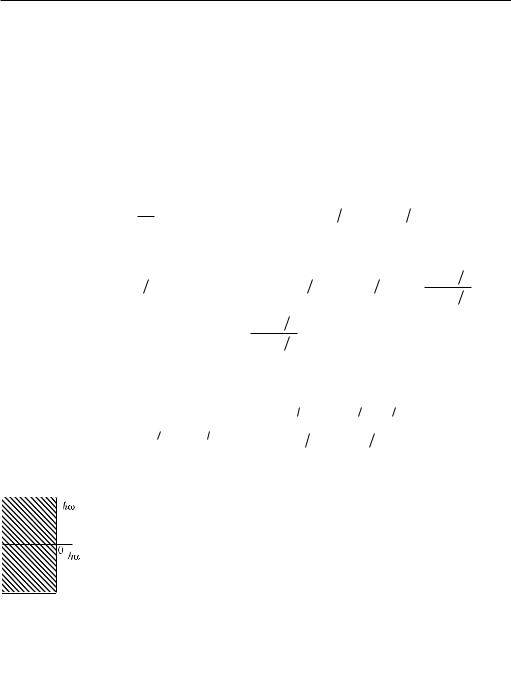
(1, 0) (рис. 9.34). Как видно из полученного неравенства, усло- |
|
|
||||||||||
вие устойчивости не налагает каких-либо ограничений на шаг |
|
Ðèñ. 9. 34 |
||||||||||
дискретизации при интегрировании абсолютно устойчивых |
|
|||||||||||
дифференциальных уравнений. Выбор шага в этом случае должен осуществ- |
||||||||||||
ляться только по соображениям точности вычислений. Заметим, что решения |
||||||||||||
74 Часть 2. Теория линейных электрических цепей
разностного уравнения неявного метода Эйлера оказываются устойчивыми и в правой полуплоскости, где решение исходного дифференциального уравнения неустойчиво. Следовательно, использование этого метода для интегрирования неустойчивых дифференциальных уравнений дает результат, не адекватный характеру истинного решения.
Рассмотренный материал показывает, что не любой метод численного интегрирования и не любой шаг дискретизации при данных значениях Χ обеспечи- вают соответствие дифференциального разностному уравнению по всем видам устойчивости. Такое соответствие может быть достигнуто при использовании неявного метода трапеций, разностное уравнение которого для уравнения (***) имеет вид
|
xn 1 |
xn hΧ (xn 1 xn ) èëè |
|
xn 1 (1 hΧ 2) 1(1 hΧ 2)xn . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соответствующее решение этого разностного уравнения имеет вид x |
n |
|
n . |
|||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Χh 2 , |
|
||||
n 1 |
|
0 |
n |
Χh 2( |
0 |
|
n 1 |
|
n ), |
|
|
(1 Χh 2) 1 Χh 2, |
|
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 Χh 2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
1 |
|
Χh 2 |
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
n |
0 |
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Χh 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Последнее выражение является приближенным представлением точного ре- |
||||||||||||||||||||||||||
шения, комбинацией явного и неявного методов Эйлера. Оно также может быть |
||||||||||||||||||||||||||
получено из следующего приближения: |
|
|
|
|
|
enΧh 2 e( Χh 2)( n) |
|
|
|
|||||||||||||||||
|
x(t |
n |
) x(nh) x |
n |
x |
0 |
enΧh |
x |
0 |
e2nΧh 2 x |
0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
0 |
(eΧh 2 )n |
(e Χh 2 ) n x |
0 |
(1 Χh 2)n (1 Χh 2) n . |
|
|
|
|
||||||||||||||
Заметим, что приближение enΧh (1 + Χh/2)n(1 – Χh/2)–n непосредственно сле- |
||||||||||||||||||||||||||
дует и из так называемой Паде-аппроксимации экспоненты. Таким образом, |
||||||||||||||||||||||||||
|
и здесь вид разностного уравнения определяется способом прибли- |
|||||||||||||||||||||||||
|
женного представления экспоненты e Χh. |
|
|
|
|
|||||||||||||||||||||
|
|
|
Область устойчивости метода трапеций, которая определяет- |
|||||||||||||||||||||||
|
ся неравенством Ε(1 – h Χ/2)–1(1 + hΧ/2)Ε < 1 èëè (1 + hΧ/2)2 < |
|||||||||||||||||||||||||
|
< (1 – hΧ/2)2, показана на рис. 9.35. Суть же отмеченного свойства |
|||||||||||||||||||||||||
|
метода трапеций состоит в том, что при чисто мнимом значении Χ |
|||||||||||||||||||||||||
Ðèñ. 9.35 |
(Χ |
j ) устойчивому решению исходного уравнения (***) соот- |
||||||||||||||||||||||||
ветствует устойчивое решение разностного уравнения, так как |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ε |
|
h Ε |
|
|||
Ε |
|
hΧ |
|
|
hΧ Ε |
|
Ε1 |
j |
|
Ε |
|
||||
|
|
|
|
|
|||||||||||
|
1 |
|
|
Ε |
|
2 Ε |
1. |
||||||||
Ε 1 |
|
|
1 |
|
Ε |
|
|
|
|
|
|
||||
|
|
Ε |
|
h Ε |
|||||||||||
|
|
2 |
|
|
2 |
|
|
|
|||||||
Ε |
|
|
|
|
|
|
Ε |
|
Ε1 |
j |
|
Ε |
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Ε |
|
2 Ε |
|
|||
Это обстоятельство позволяет использовать метод трапеций для интегрирования таких уравнений (*), матрица A коэффициентов которых содержит пару мнимых сопряженных значений. Решение в этом случае имеет составляющую

Глава 9. Расчет переходных процессов классическим методом 75
вида незатухающего гармонического колебания, что обычно и приводит к трудностям при интегрировании.
Используя рассмотренный метод, можно определить области |
||||||||||||
устойчивости и других разностных схем. На рис. 9.36 показаны |
||||||||||||
области устойчивости методов Рунге—Кутта второго и четвер- |
||||||||||||
того порядков. |
|
|
|
|
|
|
|
|
|
|
|
|
При выборе разностной схемы и шага интегрирования вопросы |
||||||||||||
устойчивости схемы должны быть согласованы с вопросами точ- |
||||||||||||
ности, поскольку адекватность схемы решаемому уравнению |
||||||||||||
только по условиям устойчивости еще не гарантирует ее «хороших» |
||||||||||||
свойств. Для примера рассмотрим решение тестового уравнения |
||||||||||||
(***) методом трапеций при Re Χ < 0; hΧ << –1. Íà n-ì øàãå |
Ðèñ. 9.36 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
(1 hΧ 2)n (1 hΧ 2) n x |
0 |
, x |
0 |
x |
0 |
. |
||
|
|
|
|
|
|
|
|
|
||||
Ïðè hΧ – | x |
n |
| |x |. Для точного решения x |
eΧnhx |
è x 0 ïðè hΧ – . |
||||||||
|
|
|
0 |
|
n |
|
|
0 |
|
|
n |
|
Таким образом, при решении данного уравнения методом трапеций шаг не может быть выбран слишком большим из-за невозможности получения требуемой точности решения. В то же время использование неявного метода Эйлера позволяет получить адекватный результат:
xn (1 hΧ) n x0 , xn 0 ïðè hΧ .
Поэтому применение неявного метода Эйлера может оказаться более эффективным при решении систем (*), все собственные значения матрицы A коэффициентов которых имеют большие по модулю и отрицательные вещественные части. Рассмотренный пример иллюстрирует сложность выбора метода, наиболее адекватного специфическим особенностям решаемого уравнения. Но определяющими принципиальную возможность эффективного применения данного метода при интегрировании определенного класса уравнений являются все же соображения устойчивости. Так, использование явных методов Эйлера и Рун- ге—Кутта для интегрирования подобных систем с большими по модулю вещественными частями собственных значений привело бы к столь существенному ограничению шага, что сделало невозможным получение достоверного результата из-за ошибок накопления или же, в лучшем случае, потребовало недопустимо больших затрат времени при реализации на компьютере.
Заметим, что для большинства уравнений состояния электрических цепей собственные значения матриц коэффициентов локализованы в левой полуплоскости, но могут быть расположены в ней достаточно произвольным образом. Поэтому для интегрирования этих уравнений целесообразно применять методы, область устойчивости которых включает всю левую полуплоскость плоскости hΧ. Такие методы называют À-устойчивыми. К таким методам относятся, например, неявные методы Эйлера и трапеций. Явные же методы Эйлера и Рунге—Кутта не À-устойчивы. Справедливы следующие утверждения:
Φникакой явный линейный многошаговый метод не является À-устойчивым;
Φне существует À-устойчивого неявного линейного многошагового метода со степенью Α > 2.
76 Часть 2. Теория линейных электрических цепей
Тот факт, что явные классические методы (Рунге—Кутта, Эйлера) не обладают À-устойчивостью, свидетельствует о том, что их использование для интегрирования систем дифференциальных уравнений приводит к большим вычислительным трудностям. На существование подобных систем уравнений, трудно поддающихся интегрированию явными классическими методами, впервые обратили внимание в 1952 г. и назвали их жесткими системами дифференциальных уравнений. В настоящее время существует специальная теория жестких уравнений и методов их решения. Большой вклад в развитие этой теории внес советский математик и электротехник Ю. В. Ракитский. Заметим, что применительно к уравнениям электрических цепей жесткость является скорее правилом, чем исключением.
9.16. Жесткость систем дифференциальных уравнений электрических цепей
При создании математических моделей электрических цепей встает проблема учета элементов с малыми значениями индуктивностей, емкостей, проводимостей, сопротивлений. Поскольку пренебрежение такими элементами может нарушить адекватность модели реальной цепи, исследователь зачастую вынужден учитывать большое число подобных элементов. Вследствие этого электрическим цепям соответствуют дифференциальные уравнения относительно высоких порядков. Причем, как правило, при описании решений подобных уравнений в интервале наблюдения требуется привлечение двух видов функций: быстроубывающих с большими производными и функций с малыми производными.
Необходимость использования таких функций для описания решений дифференциальных систем характеризует явление жесткости, а сами
подобные системы называют жесткими. Явление жесткости типично для задач теории электриче- ских цепей. Вместе с тем численное решение
жестких дифференциальных систем сопряжено со значительными трудностями. Причины таких трудностей целесообразно рассмотреть подробнее.
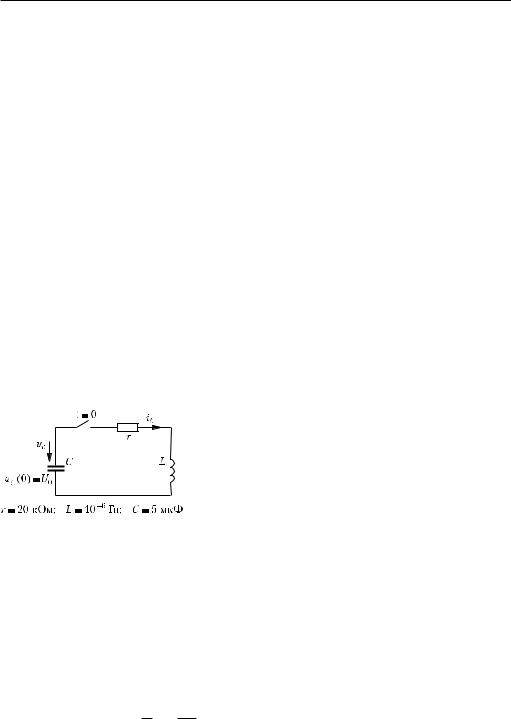
Рассмотрим процесс разряда конденсатора на активно-индуктивную цепь (рис. 9.37). Зависимость тока в цепи от времени может быть получена из решения следующего дифференциального уравнения:
d 2 iL |
|
R |
|
diL |
|
1 |
i |
|
0. |
|
|
|
|
L |
|||||
dt2 L dt |
CL |
|
|||||||
|
|
||||||||
Запишем в общем виде его решение, состоящее только из свободной составляющей iL C1eΧ1t + C2 eΧ2t , и определим корни Χ1, Χ2 характеристического урав-
нения:
Χ2 RL Χ LC1 0 Χ2 2 1010 Χ 2 1011 0. По теореме Виета,
Глава 9. Расчет переходных процессов классическим методом 77
Χ Χ |
2 |
1 LC 2 1011; Χ |
1 |
Χ |
2 |
R/L 2 1010 . |
|
|||
1 |
|
|
|
|
|
|
|
|||
Следовательно, |
|
Χ |
|
2 1010 R L ; Χ |
|
10 1 RC. |
|
|||
|
|
1 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||
Исходя из независимых начальных условий |
|
|||||||||
|
|
|
|
|
di Ε |
|
|
|
|
|
iL (0) C1 C2 0, uC |
(0) )L |
LΕ RiL (0), |
L(C1Χ1 C2Χ 2 ) R(C1 |
C2 ) U 0 , |
||||||
|
|
|
|
( |
dtΕt 0 |
|
|
+ |
|
|
найдем постоянные интегрирования: C1 –C2 U0/R. Тогда решение рассматриваемого уравнения запишем в виде
|
|
|
U |
|
|
|
R |
t |
|
1 |
t |
|
U |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
RC |
|
0 |
|
t |
|
10t |
||||||
i |
|
Γ |
|
e L |
e |
|
|
|
|
e 2 10 |
e |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
L |
|
R |
|
|
|
|
|
|
|
2 10 |
4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
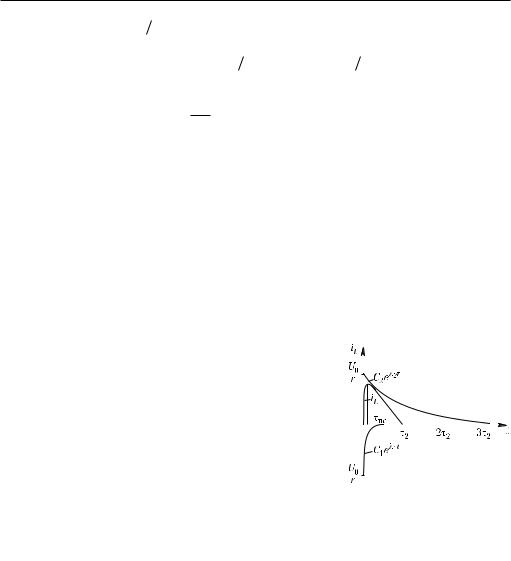
На рис. 9.38, выполненном для наглядности с искажением масштаба по оси t, выделим два участка.
Первый участок — участок пограничного слоя t Β [0, ïñ] — характеризуется быстрым изменением (большой производной) тока. Длительность этого участка определяется минимальной постоянной времени min 1 |1/Χ1 L/R. Можно принять, например, ïñ (3 ... 5) min. Второй участок, лежащий за пограничными
слоем, характеризуется |
медленным изменением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
тока. Длительность этого участка, т. е. длительность |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
наблюдения, определяется максимальной постоян- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ной времени max 2 1/Χ2 RC (обычно процесс |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
целесообразно рассматривать на интервале не бо- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ëåå (3 ... 5) max). Имеет место явление жесткости. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Следовательно, рассматриваемое уравнение, моде- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
лирующее процессы с такого рода явлением, отно- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
сится к жестким дифференциальным уравнениям. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Жестким является и уравнение состояния соответ- |
|
|
|
Ðèñ. 9.38 |
|
|
||||||||||||||||||||||||||
ствующее данной цепи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d |
|
iL |
|
|
|
2 1010 |
106 |
|
|
|
iL |
|
; |
|
iL (0) |
|
|
|
0 |
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 105 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
dt |
uC |
|
|
|
0 |
|
|
|
uC |
|
|
|
uC (0) |
|
|
|
|
U 0 |
|
|
|
|
|
|
|
|
|||||
Проанализируем трудности, возникающие при интегрировании подобных уравнений. Как было показано в § 9.15, выбор шага, обеспечивающего заданный тип устойчивости решения, должен подчиняться определенным условиям, зависящим от собственных чисел матрицы уравнений состояния, или, что то же, от корней характеристического уравнения. Например, при использовании явного метода Эйлера шаг интегрирования, обеспечивающий асимптотическую устой- чивость решения, должен удовлетворять условию 1 + hΧ < 1. Для рассмотренного выше примера это условие равносильно двум неравенствам
1 + hΧ1& 1 – h 2 1010 < 1; 1 + hΧ2 1 – h 10 < 1,
решая которые, получаем следующие ограничения на шаг: h < 10–10; h < 0,2. Следовательно, при интегрировании данной системы уравнений шаг должен быть

78 Часть 2. Теория линейных электрических цепей
ограничен значением h < 10–10, определяемым минимальной постоянной време-
íè min 1 1/Χ1 0,5 10–10 с. Длительность переходного процесса зависит от максимальной постоянной времени цепи:
(3 5) max (3 5) 2 (3 5) 1 Χ 2 (0,3 0,5) c.
Χ 2 (0,3 0,5) c.
Таким образом, применение явного метода Эйлера для интегрирования рассматриваемого уравнения на интервале T 0,5 с потребовало бы более 5 млрд (!) шагов и, соответственно, значительных затрат компьютерного времени для решения достаточно простой задачи. Учитывая ограниченность разрядной сетки реальных компьютеров и обусловленные этим ошибки округления, при соотношении шага h < 10–10 и интервала интегрирования T 0,5 с получить численное решение приведенного уравнения с удовлетворительной точностью не представляется возможным. Аналогичные трудности возникают и при использовании других явных классических методов, например методов Рунге—Кутта. Дело в том, что в явных классических методах интегрирования максимальный шаг интегрирования ограничивают по условиям обеспечения как локальной точности решения, так и его устойчивости (см. § 9.15). Поэтому в этих методах шаг интегрирования не может быть увеличен даже на тех интервалах, где решение изменяется плавно. В рассмотренном примере это относится к участку t ; ïñ (см. рис. 9.38). Действительно, точному решению данного уравнения на (n + 1)-ì øàãå
xn 1 x1n 1 x2n 1 x1n eΧ1h x2n eΧ2h
соответствует решение разностного уравнения
xn 1 x1n 1 x2n 2 ,
ãäå 1 f(Χ1 h); 2 f(Χ2 h). Таким образом, при любых значениях n, а следовательно, и t независимо от характера переходного процесса нарушение условия устой- чивости из-за увеличения шага приведет к неустойчивости численного решения.
Рассмотрим следующий пример. Пусть в некоторый момент времени tn ; ïñ, когда быстрозатухающая составляющая уже незначительна, шаг интегрирования
увеличен со значения h |
0,5 |
0,5Χ 1 0,25 10–10 с до значения h |
0,5 |
||||||||||||||||||||||
1 |
|
|
|
|
min |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
max |
0,5Χ 1 0,5 10–1 ñ, ò. å. â h |
/h |
1 |
2 109 |
раз. Рассмотрим поведение составляющей |
|||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1n 1 решения разностного уравнения xn 1 x1n |
1 x2n |
2 , соответствующей бы- |
|||||||||||||||||||||||
строзатухающей составляющей x |
1n |
eΧ1n решения x |
n+1 |
x |
1n |
eΧ1n |
+ x |
|
eΧ2n |
исходной |
|||||||||||||||
задачи (табл. 9.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Метод интегрирования |
|
|
Функция |
|
1 f (Χ.h) |
|
|
|
|
Значение x1n |
1 |
|
|
|
|||||||||||
Явный метод Эйлера |
|
|
|
|
|
1 + |
Χ |
.h2 |
|
|
|
|
|
|
10 |
9 |
) |
|
|
10 |
9 |
||||
|
|
|
|
|
|
|
|
x1n (1 |
|
|
|
|
x1n |
|
|
||||||||||
Неявный метод Эйлера |
|
|
|
|
(1 – Χ.h2)–1 |
|
|
x1n (1 109) 1 |
x1n 10 9 |
||||||||||||||||
Метод трапеций |
|
(1 + Χ1h2/2)(1 – Χ1h2/2)–1 |
|
x1n (1 109 2)(1 109 2) 1 |
x1n |
||||||||||||||||||||
Как видно из табл. 9.4, при применении явного метода Эйлера увеличение шага интегрирования h привело к резкому (в миллиард раз!) увеличению по мо-

Глава 9. Расчет переходных процессов классическим методом 79
дулю составляющей xn 1 решения xn 1 разностного уравнения и, следовательно,
к неадекватности решения разностного уравнения решению рассматриваемого уравнения. Аналогичная ситуация возникает и при использовании других явных методов численного интегрирования. Интегрирование жестких дифференциальных уравнений можно осуществлять неявными методами, шаг в которых выбирают в основном по условиям обеспечения заданной точности, и на участках плавного изменения решения он может быть увеличен. Однако необходимо заметить, что неявным методам присущи недостатки, связанные с их практиче- ской реализацией, особенно проявляющиеся именно для жестких систем. К ним относится, например, необходимость решения алгебраических, в общем случае нелинейных, систем уравнений. При этом возникают проблемы выбора численного метода решения таких систем, определения начального приближения для итерационного процесса, обеспечения сходимости такого процесса и т. д. Специфические свойства алгебраических систем, выявляемые при интегрировании неявными методами жестких уравнений состояния, например, плохая обусловленность систем, затрудняют их численную обработку. Таким образом, жесткость уравнений состояния порождает существенные вычислительные трудности их интегрирования.
Дадим, следуя Ю. В. Ракитскому, формальное определение жесткой системы
дифференциальных уравнений: |
|
|
|
|
|
|
|
|
|
x f(t, x), |
t Β[0,T]; |
|
|
|
|
||
x x(t) [x |
(t)... x |
m |
(t)]t , |
f(t, x) [f |
(t, x)... f |
m |
(t, x)]t . |
(*) |
1 |
|
|
1 |
|
|
|
||
При этом будем исходить из того, что для жестких систем значения производных решения, характеризующих скорость его изменения, вне пограничного слоя ïñ << T â N раз меньше (N >> 1), чем внутри него.
Линеаризируем правую часть последнего уравнения в окрестности начальной точки:
f(t, x) f(t, x 0 ) Ηf (x x 0 ) ... .
Ηx
Производные компонент вектора x(t) ïðè t Β >0, ïñ могут достигать значений Lmax xk(t) , ãäå L — число, удовлетворяющее неравенству 0 9 L 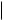
 Ηf
Ηf Ηx
Ηx 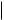
 ; здесь
; здесь

 Ηf
Ηf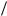 Ηx
Ηx 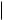
 — норма матрицы Якоби Ηf/Ηx, t Β [0, T].
— норма матрицы Якоби Ηf/Ηx, t Β [0, T].
Систему (*) называют жесткой, если при любом векторе начальных условий
найдутся такие числа ïñ < T, 0 < L |
|
|
|
Ηf Ηx |
|
|
|
, N > 1, для которых выполняется |
||||||||
|
|
|
|
|||||||||||||
неравенство |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
max x |
|
(t), |
|
k 1, 2, ..., m. |
|||||||
k |
t ;ïñ |
N |
k |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
t Β>0,T |
|
|
|||||||||
Отметим одну важную особенность данного определения, заключающуюся в том, что понятие жесткости связывается с интервалом наблюдения решения t Β [0, T]. Если жесткую на интервале t Β&>Ιϑ T] систему рассматривать лишь на подынтервале t Β&>Ιϑ ïñ ], то ее нельзя уже считать жесткой, так как здесь уже не

80 Часть 2. Теория линейных электрических цепей
наблюдается того различия в характере поведения решения, которое положено в основу понятия жесткости. Заметим, что и интегрирование подобной системы на интервале t Β [0, ïñ] не связано с какими-либо сложностями даже при использовании явных классических методов.
Если данное определение жесткости применить к линейной системе дифференциальных уравнений
|
x Ax, |
|
x Β Rm , t Β[0,T], |
||||||||
то можно прийти к следующим |
|
условиям |
äëÿ |
|
собственных значений Χj, |
||||||
j 1, 2, ..., m, матрицы A жесткой системы: |
|
|
|
||||||||
Χ |
|
eRe Χ j ïñ |
|
|
L |
, åñëè |
ReΧ |
|
0; |
||
j |
|
|
j |
||||||||
|
|
|
|
|
|
N |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Χ |
|
|
L |
, |
|
åñëè |
ReΧ |
|
; 0, |
||
j |
|
|
j |
||||||||
|
|
N |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
ãäå L max Χj ; N >>1; ïñ << T.
j
Оценим жесткость системы уравнений состояния цепи на рис. 9.37 при усло-
вии, что интервал наблюдения t Β [0, T], ãäå T 0,5 ñ, åñëè Χ |
1 |
–2 1010; Χ |
2 |
–10; |
||||||||||||||
L Χ |
2 1010. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
5 |
|
5 1/Χ |
|
2,5 10–10 ñ; N 100, получаем, что данная система |
|||||||||||
Считая |
ïñ |
min |
max |
|||||||||||||||
жесткая, поскольку для нее выполняются неравенства |
|
|
|
|
|
|||||||||||||
|
|
|
|
Χ eRe Χ j ïñ |
2 1010 e 5 |
|
L |
|
2 1010 |
1 |
; |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
N |
100 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Χ |
|
eRe Χ j ïñ |
10e 2,5 10 9 |
L |
2 108 . |
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В заключение остановимся на свойстве жестких систем, поясняющем явление жесткости и позволяющем по-новому подойти к проблеме обработки этих
систем. Для обоснования этого свойства снова обратимся к решению i |
L |
C eΧ1t + |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
+ C |
eΧ2t , t Β [0, T] жесткой системы уравнений цепи (см. рис. 9.37). Заметим, что |
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
], ãäå |
|
5/Χ |
2,5 10–10 |
|
|
|
|||||||||||
на интервале пограничного слоя t Β [0, |
ïñ |
ïñ |
с, экспоненту |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
eΧ2t e 10t можно с большой степенью точности считать равной единице. Тогда |
|||||||||||||||||||||||||||||
решение этого уравнения может быть записано в виде |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
Χ t |
|
U |
|
|
|
|
|
Χ t |
|
|
|
U |
|
|
|
|
R |
t |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|||||||||||
|
i |
|
i C |
|
C e 1 |
|
|
(1 e 1 |
) |
|
|
1 e L . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
L |
1 |
2 |
1 |
|
R |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 9.39
Глава 9. Расчет переходных процессов классическим методом 81
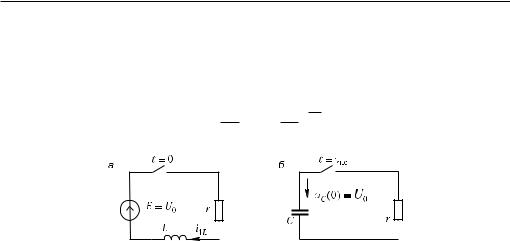
Такому решению (рис. 9.39, à) соответствует уравнение более простой цепи (рис. 9.40, à), содержащей только один накопитель энергии. На интервале, следующем за пограничным слоем t Β [ ïñ, T], составляющую решения C1eΧ1t можно считать практически равной нулю. Решение уравнения на этом интервале может быть записано в виде
1
iL i2 C2 eΧ2t UR0 eΧ2t UR0 eRC t , t Β[ ïñ ,T].
Ðèñ. 9.40
Этому выражению (рис. 9.39, á) также соответствует уравнение более простой цепи (рис. 9.40, á), имеющей только один накопитель энергии. Уравнения цепей, изображенных на рис. 9.40, à, á, описывающие, соответственно, быстрые и медленные процессы, не являются жесткими. Жесткость же исходного уравнения обусловлена объединением описания столь различных по характеру процессов. Таким образом, одним из перспективных путей обработки жестких системе уравнений является корректировка самих систем, позволяющая разделить описание быстрых и медленных процессов. В рассмотренном примере такое раздельное описание процессов могло быть выполнено априори, поскольку физиче- ская картина достаточно ясна. В том случае, когда рассматриваются жесткие уравнения состояния более сложных объектов, в которых физика процессов заранее не ясна, упрощения математических моделей на разных интервалах можно достичь лишь чисто математическими средствами. Использование процедуры корректировки математической модели, исключающей ее жесткость на отдельных временных интервалах, позволило бы эффективно применять самые простые и поэтому наиболее надежные методы численного интегрирования, такие, например, как явный метод Эйлера.
9.17. Системные методы численного решения уравнений состояния электрических цепей
В пассивных электрических цепях с резисторами переходные процессы, связанные с изменением энергетического состояния электрической цепи, постепенно затухают. В линейных электрических цепях преходящие составляющие токов и напряжений представлены суммой экспоненциальных членов, которые обычно уменьшаются со временем. Скорость уменьшения этих составляющих определяется отрицательными вещественными частями собственных чисел матрицы A. Для пассивных линейных электрических цепей чем больше по модулю вещественная часть собственного числа, тем скорее уменьшается влияние данного члена на последующий процесс.

82Часть 2. Теория линейных электрических цепей
Âжестких системах собственные числа матрицы A сгруппированы таким об-
разом, что значения их вещественных частей в одних группах 1 , …, i существенно отличаются от значений этих частей i+1, …, j других групп, в то время как внутри данной группы эти значения различаются незначительно. Для исклю- чения неопределенности будем считать, что такое положение имеет место, если
наибольшее по модулю значение i+1 ( j+1) последующей группы примерно на порядок меньше наименьшего значения i ( j) предыдущей группы.
При этих условиях можно выделить некоторый промежуток времени ïñi ( ïñj), по истечении которого влиянием экспонент, соответствующих этим группам собственных чисел, можно пренебречь. После момента времени ïñi можно пренебречь членами, соответствующими 1, …, i, а после момента времени ïñj также и членами, соответствующими i+1, …, j.
С точки зрения рационального выполнения вычислений целесообразно увеличивать шаг интегрирования по мере затухания экспонент, соответствующих большим собственным числам, определяющим малый шаг интегрирования. Однако, как показано в § 9.15, такое увеличение не может быть произведено для системы уравнений из-за нарушения условия устойчивости разностного метода.
Такое последовательное увеличение шага интегрирования может быть произведено на основе метода, названного его автором, профессором Ленинградского политехнического института Ю. B. Ракитским системным. Этот метод основан
на предложенном Ю. B. Ракитским следующем способе вычисления:
H
exp(AH), exp(A )d b,
0
ãäå H 2Nh, b [b1, b2, …, bm]t — вектор; A — квадратная матрица размерностью m m.
Легко показать, что
|
|
|
|
|
|
|
2n 1 h |
|
2n h |
|
|
|
|
|
exp(A2 |
n 1 |
h) (exp(A2 |
n |
h)) |
2 |
, |
exp(A )d |
|
exp(A )d |
|
exp(A2 |
n |
|
|
|
|
|
|
(1 |
|
h)). |
||||||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
Åñëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
h |
|
|
|
|
|
|
exp(Ah) !0 , |
|
exp(A )d Ô0 , |
exp(A )d b g 0 |
Ô0 b, |
|
|
||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
то приведенные выражения могут быть представлены в виде рекуррентных отношений
! !2 ; Ô Ô (1 ! ), g Ô b.
k 1 k k 1 k k k 1 k 1
Åñëè
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
exp(At) 1 |
|
(At)k ; |
|
|
|
|
|
||||
|
k ! |
|
|
|
|
|
||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
||
t |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
exp(A )d t 1 |
|
Ak tk 1 |
t 1 A 1 |
|
|
(At)k 1 |
, |
|||||
(k 1) |
|
(k |
1) |
|
||||||||
0 |
k 1 |
! |
|
|
k 1 |
! |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
