методичка по гидравлика № 130

Рисунок 3.2

Вакуумметрична висота вимірюється за допомогою вакуумметра, який являє собою U – подібну трубку (рисунок 3.3), заповнену важкою рідиною, наприклад, ртуттю (важка рідина береться з метою зменшення її стовпа, а отже: висоти самої трубки). Ця трубка приєднується до герметично закритої посудини, вакуум в якій потрібно виміряти.

За умовою рівноваги відносно площини порівняння О-О маємо:

Звідси	P0 +γhвак			= Pa.
			P − P			P
h		=		=			.
			aвак 0
вак			γ			γ

Знаючи показання вакуумметра hвак , визначають величину вакууму Pвак =γhвак .

Рисунок 3.3

Вакуумметрична висота збільшується по величині із зменшенням абсолютного тиску і у граничному випадку, коли P = 0 , досягає максимуму

21

				h	=			Pa	.		(3.12)
				вак.max				γ
Зокрема, для води, питома	вага			якої			γ ≈104			H	, із (3.12) одержуємо з
										м3
		H
врахуванням величини P ≈105			:	hм		=10 .				Це означає, що за рахунок
		м2
a				вак.max

вакууму воду можна підняти на висоту, не більшу ніж 10 м (за умови, що g ≈10 м/с2).

Попутно наведемо певні коментарії щодо абсолютного і надлишкового тиску. У більшості випадків представляє інтерес визначення саме надлишкового, а не абсолютного тиску, позаяк на стінки посудини та інші інженерні конструкції з одного боку може діяти тиск рідини, а з другого – атмосферний тиск. У такому разі результуючий тиск у довільній точці стінки буде складатися із абсолютного тиску за відрахуванням атмосферного, тобто буде надлишковим тиском. Тому, враховуючи, що нижче будемо мати справу в основному з надлишковим тиском, зумовимося позначувати його просто через P , а не через Pм , а абсолютний тиск – через PA .

Переходимо до тлумачення фізичного і геометричного смислу основного рівняння гідростатики (3.6).

Розглянемо частинку рідини, яка знаходиться у стані абсолютного спокою і розташована на висоті z відносно довільно вибраної площини порівняння. Позначимо її об’єм і вагу через W і γW відповідно. Повна

потенціальна енергія цієї частинки Π складається із потенціальної енергії тиску PW і потенціальної енергії положення γWz , тобто

Π = PW +γWz .					(3.13)
Поділивши рівняння (3.13) на вагу частинки γW , одержимо:
	Π	=	P	+ z.	(3.14)
	γW
			γ

Ліва частина рівняння (3.14) виражає питому, віднесену до одиниці ваги

	рідини, повну потенціальну енергію, а складові правої частини рівняння	P	і
		γ

z – питомі потенціальні енергії тиску і положення відповідно.

Отже, з фізичної точки зору рівняння (3.6) є рівнянням збереження питомої потенціальної енергії. Його енергетична інтерпретація: для усіх точок рідини, яка знаходиться у стані спокою, сума питомих потенціальних енергій тиску і положення є величина стала.

Складові рівняння (3.6) мають розмірність довжини і тому у будь-якій точці рідини можуть бути зображені певними висотами, які називаються

напорами:	P	– п’єзометричний напір;	z –	геометричний напір. Сума цих
	γ
напорів називається гідростатичним напором H :
		H = P	+ z.	(3.15)
		γ
		22

Висоту H інколи називають ще п’єзометричним напором. Геометрична інтерпретація рівняння (3.6): для усіх точок рідини, яка знаходиться у стані спокою, сума п’єзометричного і геометричного напорів є незмінною. Геометричний смисл рівняння (3.6) може бути наглядно зображений схемою на рисунку 3.4.

Рисунок 3.4

3.2 Закони Паскаля і Архімеда, їх практичне значення

Із рівняння (3.7) видно, що у будь-якій точці рідини (на будь-якій глибині h ) гідростатичний тиск P змінюється настільки, наскільки змінюється зовнішній тиск P0 . Тобто зовнішній тиск передається усім

частинкам рідини. Це явище називається законом Паскаля.

Передача тиску за допомогою рідини часто застосовується в практиці машинобудування при створенні так званих простих гідравлічних машин: гідравлічних пресів, гідроприводів, домкратів тощо. Хоча ці машини є різними за своїми конструкцією та призначенням, в усіх використовується один і той самий гідравлічний принцип, в основі якого лежить закон Паскаля.

На рисунку 3.5 показана схема гідравлічного преса. Він являє собою два сполучені циліндри з поршнями діаметрами d1 і d2 та площами

	πd 2					πd 2
ω =	1	і	ω	2	=		2	.
1	4					4
Якщо на поршень діаметром d1	діє зовнішня сила R1 , то на одиницю площі
нижньої поверхні його діє тиск

P = R1 .

ω1

Цей тиск передається за законом Паскаля усім частинкам рідини: діє на нижню поверхню великого поршня. Тому сила тиску R2 , яка діє на цей

поршень, дорівнює

R2 = Pω2 = R1 ω2 .

ω1

23

Рисунок 3.5

Звідси

	R2						2
		=	ω2	або	R2	= d2	.
	R1		ω1		R1	d1
Отже, спресовуюча сила тиску R2				більша сили			тиску R1 у стільки разів, у

скільки площа ω2 більша площі ω1 . Таким чином, за рахунок збільшення

площі другого поршня порівняно з першим маємо відповідний виграш у спресовуючій силі. Але треба зауважити, що за рахунок тертя поршнів до стінок циліндрів фактична сила R2 буде дещо менша розрахункової, тому

вводять коефіцієнт корисної дії K <1, так що

	R2		= K ω2 .
	R
			ω
1			1
Переходимо до розгляду сили гідростатичного тиску R ,				яка діє на
поверхню S зануреного в рідину			тіла об’ємом W (рисунок	3.6). При

визначенні цієї сили будемо міркувати аналогічно, як і в лекції 2 при визначенні сили тиску на поверхню довільного об’єму рідини. По аналогії з

(2.8), вирази для проекцій сили R на осі Ох, Оу,	Оz можемо написати у
вигляді:	(3.16)
Rx = −∫PnxdS;
S
Ry = −∫Pny dS;	(3.17)
S
Rz = −∫Pnz dS.	(3.18)
S

24

Рисунок 3.6

Якщо в цих рівняннях перетворити поверхневі інтеграли в об’ємні, то одержимо, згідно з (2.9):

R = −	∂P dW;	(3.19)
x
W∫ ∂x
Ry = −	∂P dW;	(3.20)
W∫ ∂y
R = −	∂P dW.	(3.21)
z
W∫ ∂z

У випадку абсолютного спокою рідини, яка знаходиться у полі дії сили земного тяжіння, маємо, ураховуючи (3.1) – (3.3),

∂P	= 0,	∂P	= 0	i	∂P	= −γ.
∂x		∂y			∂z

Якщо підставити ці значення	∂P ,	∂P	і	∂P	у відповідні рівняння (3.19), (3.20)
	∂x	∂y		∂z
і (3.21), то одержимо у кінцевому результаті:						(3.22)
Rx = 0,	Ry = 0		i		Rz =γ ∫dW =γW.
					W

Отже, рівнодіюча поверхневих сил тиску рідини на занурене в ній тіло направлена знизу вгору і намагається виштовхнути тіло з рідини. Аби пояснити фізичну природу появи цієї виштовхувальної сили, будемо виходити із наступних міркувань.

Занурене в рідину тіло уявно розділимо горизонтальною площиною О- О, яка проходить через центр мас тіла, на дві частини: верхню і нижню (рисунок 3.6). Позаяк гідростатичний тиск збільшується з ростом глибини, сила тиску на поверхню нижньої частини тіла буде, вочевидь, більшою ніж сила тиску на поверхню верхньої частини. За рахунок різниці цих сил і виникає виштовхувальна сила.

Виштовхувальна сила діє не тільки на повністю занурене тіло, а й на частково занурене. Тому під об’ємом W в (3.22) треба розуміти взагалі-то об’єм зануреної частини тіла, який дорівнює об’єму витісненої тілом рідини.

25

Вираз R =γW називається законом Архімеда, який формулюється так:

на тіло повністю чи частково занурене в рідину, яка знаходиться у полі земного тяжіння, діє виштовхувальна сила, рівна вазі витісненої тілом рідини об’ємом W . Цю силу називають силою Архімеда.

Слід зауважити, що сила Архімеда у класичному розумінні діє на занурене у рідину тіло лише за умови, що рідина знаходиться у стані абсолютного спокою, і на неї діє лише одна масова сила – сила земного тяжіння. У випадку, коли рідина знаходиться у стані відносного спокою, і на неї діють, окрім сили земного тяжіння, ще й сили інерції переносного руху, усі три проекції вектора поверхневої сили Fx , Fy і Fz , які визначаються за

відповідними формулами (3.19), (3.20) і (3.21), можуть бути відмінними від нуля. Зрозуміло, що тоді поверхнева сила тиску на тіло буде відрізнятися за своїми величиною і напрямком від звичайної сили Архімеда.

Закон Архімеда має практичне застосування, пов’язане з плаванням тіл. Об’єм рідини, витісненої плавучим тілом, називається об’ємною водотоннажністю, а його центр ваги – центром водотоннажності. У загальному випадку центр водотоннажності не співпадає з центром ваги плавучого тіла. Обидва центри при нормальному стійкому плаванні тіла розташовані на вертикальній осі – осі плавання.

Тіло тоне, якщо його вага G > R . У випадку G < R тіло спливає на поверхню. Якщо G = R , то тіло плаває на будь-якій глибині.

Площина вільної поверхні рідини, яка пересікає плавуче тіло, є площиною плавання. Периметр перетину тіла площиною плавання носить назву ватерлінії, а площа, обмежена ватерлінією, – площини ватерлінії.

Для стійкої рівноваги плавучого тіла необхідно, аби не тільки сили, але й моменти сил, що діють на тіло, були зрівноважені. Тобто рівновага наступає тоді, коли рівними є сила ваги і сила Архімеда, а сума моментів усіх сил дорівнює нулю.

Контрольні питання

1.Як пишеться основне рівняння гідростатики? Поясніть його фізичний і геометричний смисл.

2.Дайте визначення абсолютного, надлишкового (манометричного) і вакуумметричного тиску. Назвіть способи їх вимірювання.

3.Що таке п’єзометрична і геометрична висоти?

4.Що називається гідростатичним напором? В чому полягає фізична інтерпретація його?

5.Як формулюються закони Паскаля і Архімеда?

6.На чому ґрунтується принцип роботи гідравлічного преса?

7.На якому законі ґрунтуються принципи плавання тіл? Що таке плавучість і стійкість тіла?

26

ЛЕКЦІЯ 4

Сили тиску рідини на плоскі і криволінійні поверхні

4.1 Сили тиску рідини на плоскі поверхні. Центр тиску

Розглянемо простий випадок, коли прямокутна вертикальна стінка висотою Н і шириною В відгороджує деяку масу рідини (рисунок 4.1).

Визначимо повну силу	R , яка діє з боку рідини на цю стінку і зумовлена
надлишковим гідростатичним тиском або, інакше кажучи, вагою рідини.
Виділимо елементарну площадку поверхні стінки		Bdh	з центром на
глибині h , на якій	надлишковий тиск P =γh . На	цю	площадку діє
елементарна сила тиску величиною			(4.1)
	dR = PBdh = Bγhdh.

При цьому вектор цієї сили dR направлений перпендикулярно до даної елементарної площадки. Проінтегрувавши рівняння (4.1) по усій висоті стінки, знайдемо повну силу тиску рідини на стінку:

R = Bγ H∫hdh =	1	Bγ H 2.	(4.2)
0	2

Оскільки добуток ВН дорівнює площі поверхні стінки S , а величина 12 H є не що інше, як заглиблення hc , на якому знаходиться центр мас даної стінки,

формулу (4.2) перепишемо у вигляді	(4.3)
R =γhc S.

Отже, сумарна сила тиску рідини на дану стінку дорівнює добутку надлишкового тиску γhc на глибині hc занурення центра мас цієї стінки на

площу поверхні S .

	Рисунок 4.1
Ураховуючи, що добуток	hc S дорівнює	об’єму уявного циліндра,
площа основи якого дорівнює	S , а висота –	hc , формулу (4.3) можна
	27

прочитати ще так: сила, з якою рідина діє на плоску стінку, дорівнює вазі рідини в об’ємі циліндра з основою, рівною площі даної стінки, і висотою, рівною глибині занурення центра мас стінки.

Таке тлумачення рівняння (4.3) зазвичай використовують для пояснення відомого гідростатичного „парадоксу”: сила тиску рідини на дно резервуара не залежить, при одній і тій самій глибині наповнення, від форми резервуара і кількості рідини у ньому.

Рисунок 4.2

На рисунку 4.2 показані чотири різні за формою резервуари з рівновеликими днищами і з однаковою висотою наповнення, а значить, і з рівновеликими уявними циліндрами. Оскільки глибина рідини у цих циліндрах однакова, то і сила тиску рідини на дно є однаковою у всіх чотирьох випадках, недивлячись на різну форму резервуарів.

Так як γhc = Pc – надлишковий тиск на глибині занурення центра мас

стінки, формулу (4.3) можна написати ще у вигляді:
R = Pc S .	(4.4)
Сила R направлена перпендикулярно до стінки.	Точка прикладення

цієї сили до стінки називається центром тиску. Оскільки надлишковий тиск γh збільшується з глибиною h , глибина розташування центра тиску hR у

загальному випадку більша від глибини hc .

Сила гідростатичного тиску і центр її прикладення пов’язані з епюрою тиску, яка являє собою графічне зображення закону зміни тиску за глибиною. Епюра надлишкового тиску γh , яка зображена на рисунку 4.1, має вигляд

прямокутного трикутника, основа якого дорівнює γ H , а висота – Н. Площа цього трикутника

S∆ =	1	γ H 2.	(4.5)
	2

Але такий саме вигляд має формула для визначення сили надлишкового тиску, віднесеної до одиниці ширини стінки. Справді, якщо поділити рівняння (4.2) на В, то одержимо:

	R	=	1	γ H 2.	(4.6)
	B		2
		28

Отже, сила тиску рідини на стінку одиничної ширини дорівнює площі епюри надлишкового тиску у межах висоти стінки. А значить, лінія прикладення цієї сили проходить через центр мас епюри тиску. На рисунку 4.1 центр мас

знаходиться на відстані 23 H від вільної поверхні.

Згідно з (4.3) або (4.4), сила тиску рідини на плоску поверхню не залежить ні від форми цієї поверхні, ні від її орієнтації у просторі, а тільки від величини площі поверхні та від глибини занурення її центра мас під рівень вільної поверхні. Тому формули (4.3) і (4.4) справедливі не тільки на випадок вертикальної плоскої поверхні, а й на випадок плоских поверхонь різної форми і довільної орієнтації у просторі, зокрема, нахилених до горизонту.

Рисунок 4.3

Для прикладу на рисунку 4.3 зображена одна й та сама плоска поверхня ав з центром мас на глибині hc , але з різними кутами нахилу α : від π / 2 до 0.

Незалежно від кута нахилу, величина сили тиску рідини на цю поверхню буде однаковою, в цей час як глибина занурення центра тиску hR буде

зменшуватися із зменшенням кута α . Вона приймає певне значення hR > hc при α =π / 2 і дорівнює глибині hc при α = 0 .

Якщо при вивченні сили тиску рідини на плоску поверхню у загальному випадку врахувати атмосферний тиск Pa , який діє на вільну

поверхню і передається усім частинкам рідини, то у даному випадку формули (4.3) і (4.4) набувають вигляду:

RA = (Pa +γhc )S	(4.7)
і, відповідно,
RA = (Pa + Pc )S,	(4.8)

де RA – абсолютна сила дії рідини на плоску поверхню, зумовлена абсолютним тиском.

29

4.2 Сили тиску рідини на криволінійні поверхні. Тіло тиску

Задача визначення сили тиску рідини на криволінійні поверхні дещо ускладнюється порівняно з аналогічною задачею для плоских поверхонь. Це пов’язано з тим, що у випадку криволінійних поверхонь, величина, напрям і точка прикладення сили тиску залежать від конфігурації поверхні та від її орієнтації у просторі. Існуючі методи розрахунку, які відносяться до загального випадку криволінійної поверхні будь-якого виду, є досить складними і наведені у спеціальній технічній літературі. Тому нижче розглянемо лише простий частковий випадок криволінійної поверхні – циліндричну поверхню, яка зустрічається в інженерній практиці найбільш часто.

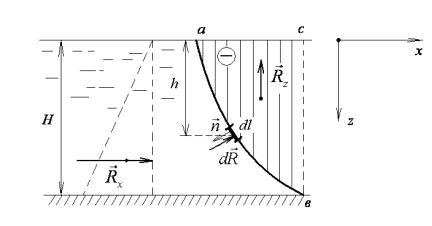
Рисунок 4.4

На рисунку 4.4, аналогічному рисунку 4.1, плоска вертикальна стінка замінена на криволінійну стінку ав, яка відгороджує деяку масу рідини глибиною Н і шириною В. Будемо вважати, що крива ав є направляючою незамкнутої циліндричної поверхні, твірна якої перпендикулярна до площини рисунка. Інакше кажучи, крива ав – проекція даної циліндричної поверхні на площину рисунка. Розташуємо осі координат Ох і Оу у площині вільної поверхні, а ось Оz направимо вертикально вниз.

При визначенні сили гідростатичного тиску на дану криволінійну поверхню будемо розглядати, як і у випадку плоскої поверхні, лише надлишковий тиск P =γh .

Виділимо на довільній глибині h елементарну площадку dS даної циліндричної поверхні:

dS = B dl ,

(4.9)

де dl – елемент довжини кривої ав.

Елементарна сила тиску dR на цю площадку дорівнює:

dR = −P n d S= −P n B d .

(4.10)

Зрозуміло, що вектор результуючої сили тиску рідини на дану циліндричну поверхню розташований у площині y = 12 B , яка є площиною симетрії і паралельна до площини рисунка. Тому, для визначення результуючої сили

30