методичка по гидравлика № 130

Якщо уявити собі деякий циліндричний шар рідини з довільним радіусом r r r0 (рисунок 7.1, б), то з боку зовнішнього сусіднього шару на

нього буде діяти сила тертя, напруження якої визначається за законом внутрішнього тертя Ньютона. У даному випадку дотичні напруження:

du							(7.1)
			dr
і направлені у бік, протилежний напрямку руху рідини.
Із (7.1) одержуємо:
du		1		dr,
а після інтегрування –
u	1		dr C.				(7.2)
Видно, що закон розподілу місцевих швидкостей u						по радіусу r пов’язаний
із законом розподілу дотичних напружень					по тому ж радіусу.
Аби знайти залежність величини					від r ,	уявно	виділимо в трубі
перетинами 1-1 і 2-2 співосний рідкий циліндр радіусом							r і довжиною l

(рисунок 7.2, а) і запишемо рівняння динамічної рівноваги цього циліндра.

Рисунок 7.2

Оскільки труба знаходиться у горизонтальному положенні, розглянемо горизонтальні сили, що діють на виділений рідкий циліндр. До них належать:

сили тиску R1 і R2 на бічні грані в перетинах 1-1 і 2-2 відповідно
R P r2 ,		(7.3)
1	1	(7.4)
R2	P2 r2 ,

де P1 і P2 – тиск в перетинах 1-1 і 2-2;

51

сила тертя F на поверхні циліндра:

F 2 rl.

(7.5)

Динамічна рівновага даного циліндра виражається у рівності нулю алгебраїчної суми усіх горизонтальних сил, що діють на нього, тому

R1 R2 F 0

або з урахуванням виразів (7.3) – (7.5):

P r2	P r2 2 rl 0.
1	2
Звідси				2l
	P1	P2			.	(7.6)
				r

Рівняння (7.6) називається основним рівнянням рівномірного руху рідини в круглій трубі. Позначимо через 0 дотичні напруження, які діють з боку

стінки труби на рідкий циліндр радіусом r0			і довжиною l . Для цього циліндра
можемо написати по аналогії з (7.6):			2l 0 .
P1 P2				(7.7)
			r
			0
Оскільки різниця тисків P1 P2 при заданій довжині l				не залежить від r ,
прирівнявши (7.6) до (7.7), одержуємо:	r
0		.		(7.8)
	r
	0

Ця залежність виражає лінійний закон зміни дотичних напружень по радіусу труби (рисунок 7.2,б), які зменшуються до нуля на осі труби, де швидкості сусідніх шарів рідини вирівнюються.

Підставивши (7.8) в (7.2) і обчисливши інтеграл, будемо мати

	u		0		r2	C.
		r		2
			0

Постійну інтегрування С визначаємо за умови, що при

C 0r0 .

2

(7.9)

r r0 швидкість u 0 :

Вираз (7.9) у кінцевому результаті набуває вигляду

u	0r0	1		r	2	.	(7.10)
				r	2
	2
			0

Це рівняння показує, що при ламінарному русі рідини в круглій трубі швидкість у живому перерізі розподіляється по параболічному закону. Максимальна швидкість на осі визначається за умовами, що при r 0 швидкість u umax :

52

												umax		0r0		.														(7.11)
Тому														2
												u umax 1						r	2		.									(7.12)
																		r	2
																	0
Знайдемо середню швидкість у живому перерізі. Згідно (5.9)
	1			1		r0	1		r	2					2							r0		r0			1 u			(7.13)
V			ud		u							2 rdr u					r			2			rdr		r3dr				.
				r2					r				max r4
						max				2									0								2	max
				0		0		0					0									0		0

Отже, середня швидкість при ламінарному русі в трубі дорівнює половині максимальної.

Знаючи закон розподілу швидкостей по живому перерізу, знайдемо коефіцієнт гідравлічного тертя . Для цього визначимо із (7.11) дотичне напруження 0 і підставимо його в (7.7), після цього поділимо одержаний

вираз на питому вагу рідини g . У результаті будемо мати з урахуванням

(7.13)

P1

P2

2l 2 2V

32 l

V ,

(7.14)

gr2

gd 2

0

де

– кінематична в’язкість рідини. Оскільки

P1

P2

є не що інше, як

втрата п’єзометричного напору на тертя hT по довжині l , вираз (7.14) перепишемо у вигляді

h		32 l	V.	(7.15)
T		gd 2

Звідси випливає важлива особливість ламінарного руху рідини: втрати напору по довжині прямо пропорційні в’язкості рідини та першій степені середньої швидкості і не залежать від шорсткості внутрішньої поверхні труби.

З другого боку, втрати напору на тертя по довжині l виражаються за формулою Дарсі, тому можемо написати

32 l	V	l	V 2 .	(7.16)
gd 2
		d 2g

Звідси одержуємо формулу для визначення коефіцієнта гідравлічного тертя

:

64 Vdv Re64 ,

де Re Vdv – число Рейнольдса.

53

7.2 Випадок турбулентного руху

Як відомо, при турбулентному русі, на відміну від ламінарного, частинки рідини хаотично перемішуються між собою. Внаслідок цього швидкість u у довільній точці потоку неперервно змінюється за часом (рисунок 7.3). Ця зміна швидкості носить випадковий характер, тому швидкість u в даний момент часу у заданій точці турбулентного потоку називається миттєвою місцевою швидкістю. Середня за часом швидкість у заданій точці називається осередненою місцевою швидкістю u . Вона визначається за формулою:

u 1 T udt, T 0

де T - відрізок часу, на якому проводиться осереднення.

Різниця між миттєвою і осередненою швидкостями у точці потоку називається пульсаційною швидкістю або просто пульсацією u u u .

Наведені вище міркування відносяться до горизонтальної місцевої швидкості u . Що стосується вертикальної і поперечної місцевих швидкостей, то їх пульсації відмінні від нуля, а осереднені вертикальна і поперечна швидкості дорівнюють нулю, так як осереднений рух рідини відбувається лише уздовж труби.

Рисунок 7.3

На відміну від миттєвих швидкостей осереднені швидкості носять регулярний характер, тому нижче мова йде про закон розподілу саме осереднених горизонтальних швидкостей по перерізу труби. Однак враховуючи, що при турбулентному режимі руху рідини в круглих трубах фізичний механізм розподілу осереднених швидкостей u значно складніший, ніж при ламінарному режимі, обмежимося лише коротким описом цього механізму, виходячи із напівемпіричної теорії турбулентності Прандтля. У

випадку турбулентного руху рідини дотичні напруження	на довільній
відстані від стінки труби у y r0 r дорівнюють:
в T ,	(7.16)
54

де в – напруження, визвані силами в’язкості; T - додаткові напруження,

зумовлені турбулентним перемішуванням мас рідини і пов’язані з пульсаціями місцевих швидкостей.

Згідно з теорією турбулентності Прандтля, весь турбулентний потік в трубі можна розділити на дві різко відмінні за структурою області: дуже тонкий в’язкий прошарок товщиною , який примикає безпосередньо до стінки і в якому рух рідини формується переважно під дією в’язких напружень в , і решту частину потоку – турбулентне ядро, де переважно

діють дотичні напруження від турбулентного перемішування в , і впливом

в’язкості можна нехтувати.

Для в’язкого прошарку робиться припущення, що в його межах y

дотичні напруження сталі і дорівнюють дотичним напруженням на стінці труби 0 . Використавши формулу Ньютона для напруження сили

внутрішнього тертя, можемо написати:

в 0 ddyu v ddyu .

Звідси

u

0

y

C

або

v

y

u

u2

C,

v

*

де величина u*

0

має розмірність швидкості і називається динамічною

швидкістю.

0 при y 0 , константа C 0 , тому

Оскільки швидкість

u

u

u*2

y

.

(7.17)

v

Для визначення турбулентних напружень T Прандтлем одержана формула:

2

2

du 2

(7.18)

T y

,

dy

де – так звана константа Прандтля-Кармана.

В напівемпіричній теорії турбулентності Прандтля робиться також

припущення, що

в

області турбулентного ядра турбулентні

напруження

T 0 const . В такому разі рівняння (7.18) можна перетворити до вигляду

	du					u*	.	(7.19)
	dy
				y
У результаті інтегрування рівняння (7.19) одержуємо:
	u			u*		ln y C.		(7.20)

Константа інтегрування С визначається за умови, що на висоті в’язкого прошарку швидкість u згідно з (7.17) дорівнює:

55

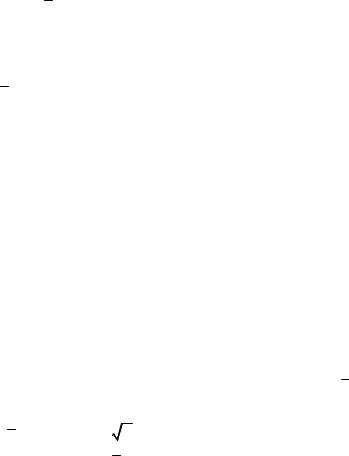
uu*2 v .

Урезультаті визначення константи інтегрування і переходу від

натурального логарифма до десяткового, формула (7.20) набуває вигляду

u	u Alg u* y			B		,	(7.21)
	*		v
		A 2,3		,
B u*			2,3 lg u*		,
	v			v

при цьому коефіцієнти А і В залежать від шорсткості труби і визначаються

експериментально. Зокрема, для		гідравлічно	гладких	труб	величини
A 5.75,	B 5.5 .
Отже, згідно з напівемпіричною теорією турбулентності Прандтля,
осереднена швидкість змінюється		за лінійним	законом	(7.17)	у межах

в’язкого прошарку і за логарифмічним законом (7.21) в області турбулентного ядра.

Для турбулентного потоку рідини в круглій трубі функціональний

зв’язок між максимальною	на осі труби					осередненою швидкістю			u	max і
середньою по перерізу швидкістю V має вигляд
		u	max V 1 1,33		u
і в залежності від величини		відношення				max		коливається у межах 1,15 1,3 ,
					V

що значно менше аналогічного відношення, рівного 2, при ламінарному русі. Що стосується закону розподілу сумарних дотичних напружень , які визначаються за формулою (7.16), то він аналогічний лінійному закону (7.8), оскільки основні рівняння рівномірного руху рідини (7.6) і (7.7) справедливі і

для турбулентного потоку в круглих трубах.

Напівемпірична теорія турбулентності Прандтля згодом була розвинена Альтшулем, у результаті чого одержана узагальнена формула (6.7) для визначення коефіцієнта гідравлічного тертя на випадок турбулентних потоків рідини в трубах.

Контрольні питання

1.За яким законом розподіляються швидкості по перерізу при ламінарному русі рідини в круглих трубах? Як пов’язані між собою середня по перерізу і максимальна на осі труби швидкості?

2.Як розподіляються дотичні напруження по радіусу труби в напірних потоках рідини?

3.Що таке миттєва і осереднена швидкості у точці турбулентного потоку?

4.Суть напівемпіричної теорії турбулентності Прандтля? Що таке в’язкий прошарок і турбулентне ядро і чим вони характеризуються?

56

ЛЕКЦІЯ 8

Рух рідини в напірних трубопроводах. Гідравлічний розрахунок простих трубопроводів

8.1 Класифікація трубопроводів

В залежності від гідравлічної схеми і методів гідравлічного розрахунку трубопроводи поділяються на прості і складні, короткі і довгі.

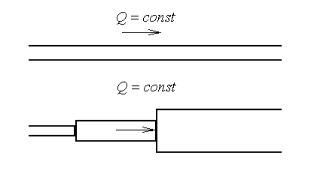
Простим називається трубопровід, який складається із однієї лінії труб, хоч би різного діаметра, але з постійною витратою по путі (рисунок 8.1). Усілякі інші трубопроводи називаються складними.

Рисунок 8.1

У випадку, коли втрати напору на тертя hт по довжині трубопроводу значно більші від місцевих втрат hм , і останніми можна нехтувати,

трубопроводи називаються довгими. Для коротких трубопроводів місцеві втрати напору сумірні з втратами по довжині, і при розрахунках потрібно враховувати обидва види втрат напору. Практично можна вважати трубопровід коротким, якщо місцеві втрати напору складають більше 10% втрат по довжині.

Окрім цього, відмітимо, що за своїм функціональним призначенням трубопроводи поділяються на усмоктувальні і нагнітальні. По усмоктувальному трубопроводу здійснюється підйом рідини насосом із джерела, яке розташоване нижче насоса. В нагнітальних напірних трубопроводах рух рідини відбувається під дією напору або тиску, який утворює насос.

Для гідравлічного розрахунку трубопроводів застосовується рівняння нерозривності (5.12) і рівняння Бернуллі (5.17) з врахуванням виразів (6.3) і (6.9) для втрат напору на тертя по довжині і в місцевих опорах відповідно.

8.2 Простий трубопровід сталого діаметра

Розглянемо напірно самопливний рух рідини в простому трубопроводі діаметром d і довжиною l . Витікання рідини може відбуватися у двох випадках: в атмосферу або під рівень (рисунок 8.2, а і б).

57

Рисунок 8.2

Для гідравлічного розрахунку даного трубопроводу потрібно насамперед скласти розрахункове рівняння. Його одержують на основі рівнянь нерозривності і Бернуллі, записаних для двох характерних перерізів потоку. Складемо розрахункове рівняння на випадок витікання рідини в атмосферу.

Намітимо перерізи 1-1 на поверхні рідини в резервуарі і 2-2 на виході із труби.

Із рівняння нерозривності

V1 1 V2 2 ,

записаного для цих двох перерізів, одержуємо:

V1		2 .	(8.1)
V
2		1

Оскільки 2 1, із (8.1) випливає, що

1

V1 V2 .

58

Тепер запишемо рівняння Бернуллі для цих перерізів з урахуванням виразів

(6.3) і (6.15)

V 2

p

V 2

p

l

V 2

V 2

(8.2)

1

1

z1

2

2

z2

2

2

.

2g

2g

d 2g

2g

Зважаючи на те, що

V1 V2 ,

p1 p2 pa

і

z1 z2 H ,

рівняння (8.2)

перепишемо, позначивши V2 V , у вигляді

l

V 2

(8.3)

H 1

.

d

2g

Це і є розрахункове рівняння для простого трубопроводу сталого діаметра у випадку витікання рідини в атмосферу.

Переходимо до складання розрахункового рівняння на випадок витікання рідини під рівень. У даному випадку, на відміну від попереднього, переріз 2-2 намітимо на поверхні рідини у другому резервуарі, тому рівняння Бернуллі можна написати у вигляді

V 2

p

V 2

p

2

l

V 2

V V2

2

1

1

z1

2

z2

2

.

(8.4)

d

2g

2g

2g

2g

У рівнянні (8.4), на відміну від (8.2), місцеві опори враховуються двома

	доданками:	V22	і	V V2 2	; перший із них враховує втрати напору на
		2g		2g

місцеві опори, розміщені до входу у другій резервуар, а другий доданок виражає за формулою Борда додаткові втрати напору, пов’язані з різким розширенням потоку на вході у другій резервуар.

Оскільки V V ,

V V ,

V V

2 V 2

1 V2

2

V 2 ,

p p

2

p

a

і

1

2

2

V

1

z1 z2 H , рівняння (8.4) можемо привести до вигляду

		l	V 2
H			1	2	.	(8.5)
		d
				2g

Порівнюючи рівняння (8.3) і (8.5), бачимо, що вони однакові за написанням, тому гідравлічні розрахунки для обох схем трубопроводу будуть теж однакові. Різниця між цими рівняннями полягає лише у тому, що при витіканні під рівень, одиниця, яка стоїть в дужках у правій частині рівняння (8.5), пов’язана з коефіцієнтом місцевого опору на виході потоку під рівень, в цей час як одиниця, яка стоїть в дужках у правій частині рівняння (8.3), пов’язана з кінетичною енергією потоку на виході із труби в атмосферу.

Виразимо розрахункове рівняння (8.3) через витрату Q , замінивши в ньому швидкість V на 4dQ2 . В результаті одержимо:

		8			1				l		2
H							1			Q		.	(8.6)
		2	g		d	4			d

При обчислюванні коефіцієнта гідравлічного тертя і коефіцієнтів місцевих опорів в (8.6) число Рейнольдса Re потрібно виразити через Q :

59

Re Vd		4Q	.	(8.7)
v		dv

Розрахункове рівняння (8.6) використовується для гідравлічного розрахунку простого трубопроводу сталого діаметра. Гідравлічний розрахунок зводиться до розв’язання трьох основних задач щодо визначення: 1. напору H , який необхідний для перекачування рідини з витратою Q по

трубопроводу діаметром d і довжиною l ;

2. витрати Q , зумовленої напором H в трубопроводі діаметром d і

довжиною l ;

3. діаметра d , який забезпечує витрату рідини Q при напорі H в

трубопроводі довжиною l .

У кожній із цих задач відносна шорсткість внутрішньої стінки труби вважається відомою.

При розв’язуванні першої задачі напір H обчислюють безпосередньо за формулою (8.6). При цьому визначення коефіцієнтів і у даній задачі

не викликає жодниих труднощів, позаяк число Re є заздалегідь відомим. Алгоритм розрахунку величини H полягає у наступному:

Q Re H.

Що стосується другої задачі, то рівняння (8.6) аналітично розв’язується відносно Q лише для досить великих чисел Re , при яких коефіцієнти і

не залежать від Re , а отже, і від Q . У даному частковому випадку одержуємо із (8.6):

Q	d 2			2gH				.	(8.8)
	4				l
		1
					d
У загальному випадку, коли	і		залежать від						Re , рівняння (8.6)

розв’язують відносно Q графічним способом або методом послідовних

наближень.

При розв’язуванні рівняння (8.6) графічним способом задають приблизні значення Q1,Q2 ,Q3 і обчислюють за виразом (8.6) відповідні

значення напору H1, H2 , H3 . Будують графік залежності H f Q (рисунок

8.3), із якого визначають шукану витрату Q , яка відповідає заданому напору

H .

Метод послідовних наближень полягає у наступному.

Припускають у першому наближенні, що величини і в (8.8) не залежать від Re , тобто величини і задаються. У цьому випадку перше наближення величини Q Q знаходять безпосередньо за формулою (8.8). Знаючи Q , визначають число Re за формулою (8.7), після чого знаходять відповідним чином другі наближення і , а отже і Q .

Кількість наближень визначається наперед заданим відхиленням і-го наближення величини Q від попереднього (і-1)-го наближення.

60