Пособие ТОКН

2

r

N

~

~

~

~

~ ~

2

S

ад

=

∑( yi −(b0 +b1x1 j +... +bn xnj +b11x

'1 j +...

+bnnx

'nj +... +bml xlj xmj ))

=

N − L

i=1

r

N

=

( ∑yi2 − Nb02 − N1b12 −... − N11b112 −... − Nmlbml2 ),

N − L

i=1

где N1 ,

N2 ,...,

Nml

– нормировочные коэффициенты. Например, для модели

(1.20) двухфакторного плана и n0 =1 получим следующее:

Sад2 = 13 (∑yi2 − 9b02 − 6b12 − 6b22 − 4b122 − 2b112 − 2b222 ).

1.7.3.Ротатабельные планы

Различие в величинах нормировочных коэффициентов для разных факторов приводит к тому, что ортогональные планы второго порядка уже не будут ротатабельными. В этом случае поверхности равной дисперсии (речь идет о дисперсии значений отклика, предсказанных уравнением модели) уже не являются сферическими, как это было для линейных планов (см. п. 1.3.4). Это приводит к тому, что дисперсия предсказания зависит от направления в факторном пространстве, т.е. ротатабельность не выполняется. В ряде случаев это явление нежелательно, например тогда, когда экспериментатору до проведения эксперимента не известно, какое направление в факторном пространстве в дальнейшем представит наибольший интерес. В связи с этим нашли широкое применение ротатабельные планы второго порядка, которые уже не будут ортогональными. Число центральных точек в таких планах уже не выбирается произвольно, звездное плечо α отлично от соответствующих ортогональных планов. Значения n0 и α для некоторых случаев даны в табл. 1.16.

		Значения α и N			Таблица 1.16
				5 (план 25)
Число факторов	2	3	4		5 (план 25–1)
Величина плеча α	1,414	1,682	2	2,378	2
Число опытов n0	5	6	7	10	6
Число опытов N	13	20	31	32	32

Увеличение числа опытов в нулевой точке (по сравнению с ортогональными планами) приводит к росту количества информации в центре плана, что требуется для выполнения условия ротатабельности. Так как свойство ортогональности не выполняется, оценки коэффициентов модели при ротатабельном планировании уже не будут независимыми, кроме того, коррелированными оказываются оценки квадратичных членов и оценки свободного члена с квадратичными. Фор-

41

мулы для расчета оценок ввиду их громоздкости не приводятся, найти их можно в работе [3]. Проверки значимости коэффициентов и адекватности модели производятся, как в п. 1.7.2, соответствующие формулы также приведены в работе [3].

1.7.4. Общие выводы Планирование второго порядка (ортогональное или ротатабельное) приме-

няют тогда, когда линейный план не позволяет построить адекватную модель и неадекватность вызвана квадратичными нелинейностями (о том, как проверить это, было сказано выше). В качестве нулевой точки нового плана обычно выбирают нулевую точку линейного плана, при этом старые опыты полностью сохраняются (они служат «ядром» нового плана) и ставятся новые опыты в звездных точках и центре плана, если это необходимо. Такие планы называются центральными композиционными, они хороши тем, что позволяют существенно сэкономить число опытов. Если, однако, точка предполагаемого оптимума лежит далеко от нулевой точки линейного плана, то центральное композиционное планирование неэффективно, так как полученная модель будет описывать область, далекую от оптимума. В этом случае применяют нецентральное композиционное планирование, выбирая в качестве нулевой точки ту точку старого плана, в которой значение отклика наиболее близко к оптимальному.

Аналогично тому, как это делалось в линейных планах, планы второго порядка можно разбить на ортогональные блоки для борьбы с дискретным дрейфом, при этом несколько изменится величина звездного плеча α.

Контрольные вопросы и упражнения

1.Поясните неформально, что означает проверка значимости коэффициентов модели.

2.Поясните свойство ротатабельности и его полезность с точки зрения практики.

3.Поясните идею проверки адекватности модели.

4.Объясните, зачем производится проверка однородности дисперсий.

5.Проверьте, что для линейной модели эффект фактора равен удвоенному значению соответствующего коэффициента.

6.Каковы будут ваши действия, если при реализации плана 23 вместо 8 опытов удалось реализовать только 6, а модель построить необходимо?

7.Покажите на примере двухфакторной нелинейной модели, как возникает взаимодействие факторов.

8.Проверьте, что для насыщенного плана определить дисперсию адекватности не представляется возможным.

9.Объясните, как получить систему смешиваний для плана 23−1.

10.К какому нежелательному явлению может привести смешивание оценок?

11.Проверьте (п. 1.4.2), что другой способ разбиения плана 22 на блоки вызовет искажение оценок b1 и b2 .

12.Поясните подробно метод Гаусса-Зейделя.

2. ОСНОВЫ ТЕОРИИ ТОЧНОСТИ

2.1. Основные понятия и определения

Точностные расчеты являются важнейшими при конструировании радиоэлектронных устройств различного назначения, поскольку обоснованное назначение допусков на параметры их элементов и правильный выбор их номинальных значений оказывают существенное влияние на главные характеристики проектируемого устройства – его тактико-технические данные, срок службы, стоимость. При этом расчету подлежат как электрические, так и механические параметры, описывающие различные узлы таких устройств.

В дальнейшем мы будет предполагать, что рассматриваемое устройство можно описать зависимостью вида

y = f (x1, x2 ,..., xn ) ,

(2.1)

где y – выходная переменная; x1, x2 ,..., xn – входные переменные. Графическая

интерпретация этой модели в виде «черного ящика» была приведена в разд. 1 (см. рис. 1.3).

В данном случае будем интерпретировать входные переменные как параметры элементов, из которых это устройство сделано и которые влияют на выходную переменную. Выходная переменная (выходной параметр) – это количественный показатель, характеризующий выполнение устройством своей функции. Например, если устройство – это усилитель, то входными параметрами являются сопротивления резисторов, емкости конденсаторов и т.п., выходным параметром – коэффициент усиления. При наличии у рассматриваемого устройства нескольких выходных параметров оно описывается совокупностью зависимостей вида (2.1).

При проектировании устройства предполагается, что значения параметров его элементов могут отличаться от номинальных из-за каких-либо нарушений технологического процесса их изготовления. В результате значение выходного параметра также отличается от номинального, т.е. имеется некоторая погрешность. Одной их главных задач теории точности является установление соотношений между характеристиками погрешностей входных и выходного параметров. Введем ряд определений, необходимых для дальнейшего.

Абсолютная погрешность – разность между реальным и номинальным значениями параметра x: x = x − x0 , где x0 – его номинальное значение.

Более информативной является относительная погрешность	х , поэто-
	х0

му дальше будем рассматривать этот вид погрешностей. Для простоты будем обозначать ее хх , имея в виду, что деление осуществляется на номинальное значение параметра x.

43

Систематическая погрешность – погрешность, которая входит в результаты измерений и вычислений по известному закону; в простейшем случае она постоянна.

Случайная погрешность – погрешность, которая входит в результаты измерений и вычислений по случайному закону.

В общем случае погрешности параметров элементов и устройства имеют как систематические, так и случайные составляющие, в расчетах необходимо учитывать обе эти составляющие.

Важнейшими характеристиками погрешностей являются допуск и разброс. Допуск – разность между пределами, в которых должно находиться значение параметра элемента или устройства согласно техническим условиям. Допуск может быть односторонним, когда ограничивается только один из пределов, при этом второй равен +∞ или −∞; в случае двустороннего допуска ограничены оба предела. Полем допуска принято называть область значений па-

раметра в пределах его допуска.

Разброс – разница между пределами, в которых может находиться значение параметра. Полем рассеивания называется множество всех значений, которые может принимать параметр.

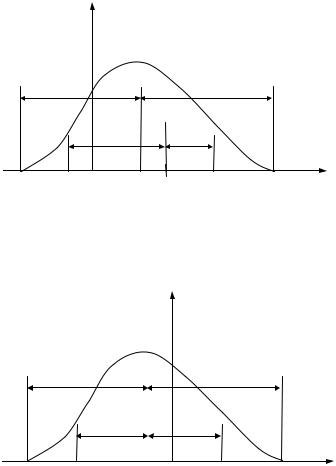
Проиллюстрируем графически некоторые из приведенных понятий. На рис. 2.1 приведены характеристики для абсолютной и относительной погрешностей. Символом ϕ(x) обозначена плотность вероятности значений параметра

x, рассматриваемого как случайная величина; ее можно интерпретировать как частоту (частость) появления тех или иных значений параметра или его относительной погрешности. Символом xc на рис. 2.1, а обозначена середина поля

допуска параметра, l(x) – величина половины разброса, δ−(x) и δ+(x) – отри-

цательное и положительное допустимые отклонения соответственно.

Рисунок 2.1, б повторяет предыдущий рисунок для относительных погрешностей и согласован с ним; его начало координат теперь соответствует но-

минальной точке, E( xx) – координата середины поля допуска. Поскольку в дальнейшем мы будем иметь дело только с относительными погрешностями,

условимся вместо аргумента	y	или	xi	записывать индекс y или i у соот-
	y		x
			i

ветствующей характеристики, например E y или δi .

Если δ+ и δ− – верхнее и нижнее предельные отклонения относительной

погрешности соответственно, то характеристики поля допуска рассчитываются следующим образом:

	E =	1	(δ+ + δ−) ,	δ =	1	(δ+ −δ−) .
		2			2

44

ϕ(x)

l(x)

l(x)

δ− (x) δ+ (x)

xс x0

x

а

		ϕ(		x)
			x
l(	x)						l(	x)
	x	x)					x)	x
	δ(					δ(
		x					x
		E(		x)				x
				x				x

б

Рис. 2.1. Иллюстрации к основным понятиям

Например, если R = 10 K±10%, то ER = 0 , δR =10% ; если С = 12 нФ+−1020%% , то EC = 5% , δC =15 %. В первом случае допуск называется симметричным,

во втором – несимметричным.

Основной задачей при расчете допусков является установление зависимости между характеристиками полей допусков входных параметров и характеристиками поля рассеивания выходного параметра – задача анализа допусков. Более сложной является обратная задача – синтеза допусков, когда по заданному допуску на выходной параметр требуется рассчитать номинальные значения и допуски на входные параметры так, чтобы обеспечивалась заданная точность выходного параметра. Рассмотрим обе задачи, причем задачу анализа раньше, так как она проще первой и дает необходимый материал для решения второй.

45

2.2. Вывод модели погрешностей

Прежде всего, необходимо установить зависимость между погрешностями входных и выходного параметров. Начнем с простейшего случая, когда входной параметр один и функция, описывающая устройство, имеет вид y = f (x) . Предполагая, что она дифференцируема на интересующем нас ин-

тервале, разложим ее в ряд Тейлора в окрестности номинального значения параметра x0 :

у = f (x0 ) +

∂f

(x − x0 ) +

∂x

(2.2)

1

∂2 f (x − x

1

∂k −1 f

+

0

)2

+... +

(x − x

0

)k −1 + R (x),

2! ∂x2

(k −1)!

∂xk −1

k

где Rk (x) – остаточный член, для которого выполняется следующее условие:

| Rk (x) |≤	| x − x0 |k	sup		∂k f (z)		, a ≤ z < x ,
	k!			∂xk

где a – нижняя граница интервала, на котором рассматривается функция f. Допустим, что значение параметра x изменилось на х: х0 → х0 + х, то-

гда значение выходного параметра также изменится: y0 → у0 + у. Подставим эти новые значения в формулу (2.2) при k = 2:

у0	+ у = f (x0 ) +	∂f	(x0	+ x − x0 ) + R2 (x) = f (x0 ) +	∂f	x + R2 (x) .
		∂x			∂x

Для того чтобы в последнем равенстве можно было пренебречь слагаемым R2 (x) и, следовательно, получить выражение, линейное относительно прира-

щения х, требуется, чтобы выполнялось условие

	|	∂f	x |>>	x2	sup	∂2 f (z)	, x0	≤ z < x0 + x ,
		∂x		2!		∂x2

или

| x |<< 2		∂f		sup	∂2 f (z)	, x0	≤ z < x0 + x .
		∂x			∂x2

46

Соблюдение этого условия дает нам с учетом соотношения у0 = f (x0 ) приближенное равенство, которое будем записывать как точное:

y =	∂f	x.	(2.3)
	∂x

Процедура, с помощью которой была получена последняя формула, называется линеаризацией: нелинейная функция в ограниченной окрестности точки x0 заменена отрезком прямой, совпадающим с касательной к функции в этой

точке (рис. 2.2).

y

y0

x

x0

Рис. 2.2. Иллюстрация процедуры линеаризации

Отметим, что равенство (2.3) может быть получено из других соображений. Найдем дифференциал функции y = f (x)

dy = ∂∂fx dx

и перейдем к конечным приращениям, заменяя dx и dy на x и y соответст-

венно. При таком подходе затушевывается существо производимого процесса линеаризации, но он удобен с математической точки зрения.

В выражении (2.3) перейдем от абсолютных погрешностей к относительным, поскольку, как уже говорилось, они более информативны:

у		∂f x0		x
у0	=	∂x		x0 .
			f (x0 )

В общем случае, когда устройство описывается моделью (2.1), основная идея вывода искомой зависимости остается прежней: производится линеаризация функции в n-мерном пространстве путем замены ее касательной гиперплоскостью, что дает соотношение для абсолютных погрешностей. Его можно по-

47

лучить путем нахождения полного дифференциала функции и перехода к конечным приращениям:

dy = ∑	∂f	dxi ,	y = ∑	∂f	xi
				∂xi
	∂xi

(пределы суммирования здесь и далее будем, как правило, опускать). После этого переходим от абсолютных погрешностей к относительным:

y

n

xi

= ∑Bi

,

(2.4)

y

xi

i =1

где коэффициент влияния

B

=

∂f

x

(2.5)

∂xi

f

i

рассчитывается при номинальных значениях параметров.

Пример 2.1. Последовательное соедине-

R1

R2

ние резисторов (рис. 2.3).

Рис. 2.3. Последовательное

В результате простых расчетов получаем:

соединение резисторов

y

= R1 + R2 ,

B = (∂(R + R

2

) / ∂R )

R1

=

R1

,

R

+ R

R

+ R

1

1

1

2

2

1

1

по аналогии,

B2 =

R2

.

R1

+ R2

Пример 2.2. Плоский конденсатор с обкладками в виде кругов (рис. 2.4).

Исходные данные: d – расстояние между обкладками; r – радиус обкладки; ε – диэлектрическая проницаемость диэлектрика. По известным законам получаем формулу для емкости

Рис. 2.4. Плоский конденсатора:

конденсатор

С = С0 r 2ε , d

48

где символом С0 обозначены все несущественные для рассматриваемой задачи константы. Используем формулу (2.5):

B

=C

2rε rd

= 2,

B

=C

r2 εd

=1,

B

d

= −1.

0 d C

r2ε

0 d C

r2ε

r

0

ε

0 0

Легко видеть, что коэффициенты влияния совпадают с показателями степеней у соответствующих параметров; такая закономерность характерна только для случая, когда выходной параметр равен произведению параметров элементов. Уравнение для расчета погрешностей принимает следующий вид:

yy = 2 rr + εε − dd .

2.3. Методы определения коэффициента влияния

Для проведения точностных расчетов необходимо, прежде всего, уметь находить коэффициенты влияния. Рассмотрим детально несколько методов.

2.3.1. Аналитический метод Метод используется в тех случаях, когда с достаточной для практики точ-

ностью известна зависимость, описывающая рассматриваемое устройство. В этом случае расчет производится непосредственно по формуле (2.5). В некоторых частных случаях расчеты существенно упрощаются, например, когда выходной параметр равен произведению параметров элементов (этот случай был рассмотрен в примере 2.2).

2.3.2. Экспериментальный метод Метод используется в тех случаях, когда зависимость, которая должна

описывать устройство, отсутствует либо возникают затруднения при ее нахождении. Возможны две основные разновидности этого метода.

1. Метод поочередного варьирования каждого параметра. Из линейности уравнения (2.4) относительно погрешностей следует, что если все параметры, кроме i-го, будут равны своим номинальным значениям, а этот параметр отклонится от номинального на xi , то уравнение (2.4) будет содержать только одно

слагаемое, в результате чего расчеты существенно упрощаются.

Таким образом, для нахождения всех коэффициентов влияния каждый параметр поочередно отклоняют от номинального значения на небольшую величину xi , измеряют величину отклонения выходного параметра y и по формуле (2.4)

производят вычисления. Например, для первого параметра получаем следующее:

yy = B1 xx1 ,

1

49

откуда

B	=	y	y	.
1		x1	x1

2. Многофакторный эксперимент. Для повышения точности вычислений коэффициентов влияния воспользуемся методами теории планирования эксперимента, рассмотренными в разд. 1. Основная идея здесь состоит в следующем. Проводится полный или дробный факторный эксперимент, по итогам которого строится линейная модель рассматриваемого устройства:

~	~
y = b0 +b1x1	+... +bn xn .

По формулам (1.4) производится переход от кодированных факторов к исходным и далее на основе модели в исходных факторах аналитическим методом определяются коэффициенты влияния (приведем их без детального вывода):

B	=	bi		xiв + xiн	,	i = 1, 2,…,n.	(2.6)
i		b0		xiв − xiн

где xiв и xiн – верхнее и нижнее значения i-го фактора при его варьировании.

Известно, что в многофакторном эксперименте точность определения коэффициентов влияния выше, чем в однофакторном, если число опытов примерно одинаково. Это объясняется тем, что в формуле (2.6) использованы результаты всех опытов, в то время как в предыдущей формуле – только двух.

2.3.3. Экспериментально-расчетный метод Так называется метод определения коэффициентов влияния с помощью

ЭВМ, который используется в системах автоматизированного проектирования радиоэлектронных устройств. С развитием вычислительной техники и в связи с разработкой математических моделей практически для всех существующих электронных компонент два рассмотренных выше метода практически потеряли свое значение и в настоящее время редко используются. Их заменил экспе- риментально-расчетный метод, суть которого состоит в следующем.

В ЭВМ в том или ином виде вводится описание исследуемого устройства; как правило, здесь используется не непосредственное аналитическое описание типа (2.1), а описание в виде совокупности элементов, из которых построено устройство (резисторы, конденсаторы, микросхемы), и их связей. Далее программным путем (по методике однофакторного или многофакторного эксперимента) меняются значения входных параметров и на основе имевшегося в ЭВМ описания устройства рассчитываются значения выходного параметра. После этого по формуле (2.6) или (2.7) (в зависимости от вида вычислительного эксперимента) производится расчет коэффициентов влияния.

50