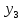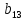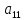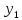Глава 1. Системы одновременных уравнений

§ 1.1 Системы уравнений, используемые в эконометрике

Предметом статистического исследования в экономических науках являются сложные системы. При использовании уравнений регрессии предполагается, что аргументы можно менять вне зависимости друг от друга. Но данная операция была бы неверной, так как изменение одной переменной влечет за собой изменение и других. Ее изменение поведет за собой изменение во всей системе. Следовательно, уравнение множественной регрессии не может показать истинного влияния отдельных признаков на результат исследования. Вследствие этого в последнее десятилетие в системе экономических, биометрических, социальных наук остро встал вопрос об изучении связей между переменными в системе одновременных уравнений. Одним из примеров использования систем одновременных уравнений в экономике является модель спроса и предложения. Если изучается модель спроса как соотношение цен и количества товаров, то одновременно для его прогнозирования необходима модель предложения товаров, в которой будет предложена взаимозависимость между количеством и ценой предлагаемых благ. Еще одним из примеров использования систем одновременных уравнений служит модель оценки эффективности производства. При построении данной модели нельзя пользоваться моделью рентабельности, ее следует дополнить моделью производительности труда, а также моделью себестоимости единицы продукции.

Большая нужда в использовании систем одновременных уравнений возрастает при переходе с микроэкономического уровня к макроэкономическому. Так как в построении модели национальной экономики используются системы уравнений, включающие в себя: функции потребления, чистого дохода, инвестиций, заработной платы и тд. Это объясняется прежде всего тем, что макроэкономические показатели, которые являются основополагающими показателями состояния экономики страны тесно взаимосвязаны. Так, расходы на конечное потребление зависят от валового национального дохода, а валовый национальный доход в свою очередь рассматривается как функция инвестиций.

Системы эконометрических уравнений при проведении исследований могут быть построены по-разному.

Может быть система независимых уравнений, то есть каждая зависимая переменная (y) рассматривается как функция одного и того же набора факторов (x):

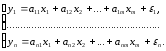
Количество независимых переменных в каждом уравнении может меняться. Допустим модель вида:

тоже является системой независимых уравнений, единственное отличие в том, что количество факторов, входящих в данную систему видоизменен. Отсутствие того или иного фактора может выступать как причина нецелесообразности системы или того, что данный фактор оказывает несущественное значение на исходный результат.

Каждое уравнение системы может рассматриваться в отдельности от системы, так как является уравнением регрессии. Для нахождения параметров уравнения пользуются методом наименьших квадратов. Так как, не всегда известно, что факторы полностью объясняют зависимую переменную или нет, в уравнениях присутствует свободный член . Поскольку фактические значения зависимой переменной отличаются от теоретических на случайную ошибку, то во всех уравнениях присутствует случайная величина ошибки.

В конечном счете система независимых уравнений, состоящая из трех зависимых переменных и четырех факторов примет вид:

Однако если зависимая переменная y одного уравнения выступает в качестве независимой переменной в другом, то модель можно построить в виде системы рекурсивных уравнений:

В такой системе уравнений переменная y включается в каждое последующее уравнение в качестве факторов, вне зависимости с набором собственных факторов x. Примером такой модели может служить модель производительности труда и фондоотдачи вида:

где – производительность труда;

–фондоотдача;

–фондовооруженность труда;

–энерговооруженность труда;

–квалификация рабочих. [5, с. 180]

Как было сказано ранее, каждое уравнение можно рассматривать по отдельности, и его параметры находятся методом наименьших квадратов (МНК).

Наибольшее использование в эконометрических исследованиях получила система одновременных уравнений. Она имеет вид:

Данная система уравнений называется системой одновременных уравнений, так как в ней одни и те же переменные могут быть зависимыми в одном уравнении и в тоже время быть независимыми. В эконометрике данная система уравнений называется также структурной формой модели. В отличие от предыдущих систем уравнений, уравнения модели данного типа не могут рассматриваться самостоятельно, а обычный МНК, использовавшийся для нахождения параметров в данном случае неприменим. В связи с этим используются специальные приемы оценивания.

В качестве примера системы одновременных уравнений можно рассмотреть модель изменения цены и заработной платы:

где 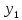– темп изменения месячной заработной платы;

–темп изменения цен;

–процент безработных;

–темп изменения постоянного капитала;

–темп изменения цен на импорт сырья.

Система одновременных уравнений обычно состоит из эндогенных и экзогенных уравнений.

Эндогенные переменных в ранее рассмотренных примерах обозначены через y. Это зависимая переменная, количество которых равно количеству уравнений в системе.

Экзогенные переменные – это независимые переменные (факторы), влияющие на эндогенные переменные, но не зависящие от них.

Если смотреть с математической точки зрения, главным отличием эндогенных и экзогенных переменных является то, что экзогенные переменные не коррелируют с ошибками регрессии, в то время как эндогенные переменные коррелируют.

Простейшая форма систем одновременных уравнений имеет вид:

где – эндогенные переменные;

–экзогенные переменные.

Разделение переменных на экзогенные и эндогенные напрямую зависит от теоретической направленности модели. Используемые переменные в одних уравнениях могут быть экзогенными, а в других эндогенными. Вместо экзогенных переменных в некоторых эконометрических моделях могут использоваться эндогенные переменные, полученные в предыдущий период, то есть лаговые переменные. Таким образом, спрос текущего года может зависеть не только от факторов данного года, но и от положения в предыдущем году. Конструктивная форма модели позволяет представить, как малейшие изменения эндогенной переменной может повлиять на конечный результат, то есть эндогенную переменную. Рационально в качестве экзогенных переменных выбирать такие переменные, которые поддаются регулированию. Работая ими, всячески меняя, заранее можно выявить целевые значения зависимых переменных.

В модели, в правой части имеются коэффициенты при эндогенной и экзогенной переменных исоответственной. Эти коэффициенты называются структурными коэффициентами модели. В уравнениях данной системы отсутствует свободный член, так как все переменные модели представлены в виде отклонения от среднего уровня, то есть, а.

Как принято считать в теории, использование МНК для оценивания коэффициентов модели, выводит неточные смещенные значения. Вследствие этого для нахождения значений структурных коэффициентов необходимо привести модель в приведенную форму.

Приведенная форма модели представляет собой систему функций, зависимости эндогенных переменных от экзогенных:

где – коэффициенты приведенной формы модели.

По своей структуре приведенная форма системы одновременных уравнений ничем не отличается от системы независимых уравнений, оценка параметров которых находится через обычный МНК. Используя МНК можно оценить δ, далее оценить значения эндогенных переменных через экзогенные. Коэффициенты приведенной формы представляют собой нелинейные функции коэффициентов структурной формы модели. Применим данное положение к простейшей структурной модели, выразим коэффициенты приведенной формы через коэффициенты структурной формы модели. Для структурной модели вида:

(1.1.1)

приведенная форма имеет вид:

(1.1.2)

где из (1.1.1) можно выразить следующим образом:

Тогда система одновременных уравнений примет вид:

Отсюда имеем равенство:

или

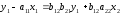
Тогда

Или

Таким образом, первое уравнение структурной формы модели представлено в приведенной форме вида:

Из данного уравнения вытекает, что коэффициенты приведенной формы модели являются нелинейными соотношениями коэффициентов структурной формы, т.е.

и

Таким же способом можно показать, что коэффициенты второго уравнения структурной формы модели нелинейно связаны с коэффициентами приведенной модели.

Эконометрические модели обычно содержат в системе не только уравнения, отражающие взаимосвязь между отдельными переменными, но и выражения, показывающие тенденции развития явления, а также разного вида тождества. Так, в 1947 г., проводя исследования зависимости потребления (c) от дохода (y), T.Khanelvo предложил одновременно учитывать тождество дохода. В таком случае модель выглядит таким образом:

где x – инвестиции в основной капитал и в запасы экспорта и импорта;

a и b – параметры линейной зависимости c от y.

При оценке должны учитываться тождество дохода, в отличие от параметров обычной линейной регрессии. [5, с. 184]

На этапе перехода от приведенной формы к структурной сталкиваются с проблемой идентификации. Понятие идентификации означает единственность соответствия между приведенной и структурной формами модели.

В качестве примера рассмотрим проблему идентификации для модели с двумя эндогенными переменными. Пусть структурная форма модели имеет вид:

где – совместные зависимые переменные.

Из второго уравнения выразим 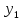следующим образом:

Из этого следует, что система будет состоять из двух уравнений для переменной с одним и тем же набором переменных, но с разными коэффициентами при них:

Наличие двух вариантов расчета структурных коэффициентов одной и той же модели связано с неполнотой ее идентификации. Структурная модель, представленная в полной мере, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n(n-1+m) параметров, а приведенная форма в полном виде состоит из nm параметров. Так как структурная форма содержит больше параметров, чем приведенная это не может привести к единственности решения. Для того, чтобы получить единственность решения некоторые параметры в структурной форме, из-за слабой взаимосвязи признаков с эндогенной переменной необходимо приравнять нулю. Тем самым уменьшится количество структурных коэффициентов модели.

По идентифицируемости структурные модели можно подразделить на:

• идентифицируемые;

• неидентифицируемые;

• сверхидентифицируемые. [6,c.44]

Модель называется идентифицируемой, если количество параметров структурной модели равно количеству параметров приведенной модели, то есть структурные коэффициенты определяются однозначно по коэффициентам приведенной формы.

Модель является неидентифицируемой, если количество приведенных коэффициентов больше количества структурных коэффициентов и в итоге структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы.

Модель является сверхидентифицируемой тогда и только тогда, если число приведенных коэффициентов больше числа структурных коэффициентов. [6, c.46] В этом случае может существовать несколько значений структурного коэффициента. Сверхидентифицируемая модель может быть двух типов:

1. все уравнения модели сверхидентифицируемы;

2. система содержит на ряду с идентифицируемыми моделями модели, которые сверхидентифицируемы.

Структурная модель обычно состоит из системы совместных уравнений, каждое из которых нужно проверять на идентификацию. Модель является идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно уравнение неидентифицируема, то говорят, что вся модель неидентифицируема. Также и со сверхидентифицируемостью. Для того, чтобы модель была сверхидентифицируемой необходимо, чтобы хотя бы одно из уравнений было сверхидентифицируемым.

Условие идентифицируемости проверяется для каждого уравнения системы. Для того, чтобы система была идентифицируемой необходимо, чтобы количество переменных, отсутствующих в данном уравнении, но содержащиеся в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в j-ом уравнении системы через Н, а число экзогенных переменных, содержащиеся в системе, но не входящие в данное уравнение через D, то для идентифицируемости вытекает следующее правило:

D + 1 = H – уравнение идентифицируемо;

D + 1 < H – уравнение неидентифицируемо;

D + 1 > H – уравнение сверхидентифицируемо.

Проверим следующую систему одновременных уравнений на идентифицируемость:

(1.1.3)

Первое уравнение идентифицируемо, так как в нем содержится три эндогенные переменные - то естьH=3, две экзогенные переменные - , число отсутствующих экзогенных переменных равно двум -, то естьD=2. Следовательно имеем равенство: D + 1= H, то есть 2 + 1 = 3, что в свою очередь означает идентифицируемость уравнения.

Во втором уравнении системы H = 2 () иD = 1 (). Правило идентифицируемости выглядит следующим образом:D + 1 = H, то есть 2 + 1 = 3, что означает, что уравнение идентифицируемо.

В третьем уравнение системы H = 3 (),a D = 2 (). Тогда по правилу идентифицируемостиD + 1 = H, и это уравнение идентифицируемо. Таким образом, система (1.2.1) целиком и полностью идентифицируема.

Рассмотренное счетное правило идентифицируемости является необходимым условием, но ни в коем случае не достаточным. Более точное условие определяется если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно составить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем количество эндогенных переменных в системе, без учета рассматриваемого уравнения.

Целесообразность проверки выполнения условия идентификации модели через определитель матрицы коэффициентов отсутствующих в данном уравнении, но присутствующих в других обусловлено тем, что возможна ситуация, когда для каждого уравнения выполняется правило идентифицируемости, но определитель матрицы рассмотренных коэффициентов равен нулю. В таком случае соблюдается только необходимое условие, но не достаточное.

В качестве примера рассмотрим следующую структурную модель:

(1.1.4)

Проверим каждое уравнение до необходимое и достаточное условие идентификации. Для первого уравнения H = 3 () иD = 2 (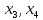отсутствуют), таким образом,D + 1 = H, а из этого следует, что необходимое условие идентифицируемости выполнено, поэтому уравнение идентифицируемо. Для проверки на достаточное условие идентифицируемости необходимо заполнить следующую таблицу для коэффициентов переменных, отсутствующих в первом уравнении:

Уравнения	Переменные
2 3 0 0

Ввиду этого видно, что достаточное условие идентификации не выполнено и первое уравнение нельзя считать идентифицируемым.

Для второго уравнения H = 2 (),D = 1 (отсутствует ). Согласно необходимому условию идентифицируемостиD + 1 = H, а это говорит о том, что уравнение идентифицируемо. При проверке на достаточное условие идентифицируемости можно убедиться, что коэффициенты при отсутствующих во втором уравнении переменных составят:

Уравнения	Переменные
1 3 -1

Согласно таблице, определитель матрицы неравен нулю, а ранг матрицы равен 2, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее, чем число эндогенных переменных в системе без одного. Следовательно, второе уравнение идентифицируемо.

В третьем уравнении системы H = 3 и D = 2, т.е согласно счетному правилу идентификации, уравнение идентифицируемо. Но проверив на достаточное условие можно убедиться в обратном. Для этого составим таблицу коэффициентов при отсутствующих в третьем уравнении переменных, в которой определитель равен нулю:

Уравнения	Переменные
1 0 0 2

Из таблицы видно, что в третьем уравнении нарушается достаточное условие идентифицируемости, значит уравнение неидентифицируемо. Если же рассматривать структурную модель в целом, то можно сделать вывод, что выполнение необходимого условия идентифицируемости не дает полного права утверждать, что модель идентифицируема, проверка достаточного условия обязательна. [5,с. 191]

Часто в эконометрических моделях наряду с уравнениями, параметры которых статистически должны быть оценены, используют балансовые тождества коэффициенты которых равны . В таком случае хотя само тождество проверки на идентификацию не требует, но в проверке структурных уравнений тождество участвует.

В качестве примера, рассмотрим эконометрическую модель экономики страны:

где – расходы на конечное потребление данного года;

–валовые инвестиции в текущем году;

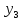–расходы на заработную плату в текущем году;

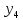–валовый доход за текущий год;

–валовый доход предыдущего года;

–государственные расходы текущего года;

А – свободный член управления;

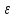–случайные ошибки.

В этой модели четыре эндогенные переменные (). Причем последнее уравнение задано тождеством. Таким образом, статистическое решение и проверка на идентификацию необходима для первых трех уравнений. Модель содержит две предопределенные переменные – экзогеннуюи лаговую. Как правило, при составлении модели на несколько лет или для совокупности регионов на один год для эндогенных переменных () вводят свободный член (), значение которого активизирует влияние неучтенных в уравнении некоторых факторов и не влияет на идентифицируемость модели. Поскольку фактические данные могут отличаться от теоретических в модель включают случайную составляющую вместо тождеств. Эти случайные величины называются случайными ошибками, обозначены черези они никак не влияют на вопрос идентификации модели.

В рассмотренной ранее модели первое уравнение системы является идентифицируемой, так как H = 3 и D = 2, при этом выполняется необходимое условие идентификации (D + 1 = H). Помимо этого, выполняется и достаточное условие, то есть ранг матрицы равен 3, а определитель ее не равен 0. Это видно из нижеприведенной таблицы:

Уравнения
2	-1		0
3	0		0
4	1	0	1

Второе уравнение данной системы также идентифицируемо: H = 2 и D =1, то есть необходимое условие выполнено и D + 1 = H, также выполнено и достаточное условие идентифицируемости: ранг матрицы A равен 3, а определитель по нижеприведенной таблице равен :

Уравнения
1	-1		0
3	0		0
4	1	-1	1

Аналогично и третье уравнение системы идентифицируемо: H = 2, D = 1, D + 1 = H, определитель матрицы равен 1, а ранг матрицы равен 3:

Уравнения
1	-1	0	0
2	0	-1	0
4	1	1	1

Идентификация уравнений достаточно сложна и не ограничивается вышеизложенным. Также могут накладываться и другие ограничения. Например, могут накладываться ограничения на дисперсии и ковариации остаточных величин. [5,c. 193]

В зависимости от видов систем одновременных уравнений, для оценивания коэффициентов структурной модели используют различные методы. Наиболее часто в литературе рассматривают следующие методы оцениваю коэффициентов структурной модели:

• косвенный метод наименьших квадратов;

• двухшаговый метод наименьших квадратов;

• трехшаговый метод наименьших квадратов;

• метод максимального правдоподобия с полной информацией;

• метод максимального правдоподобия с ограниченной информацией.

Косвенный и двухшаговый МНК используются как традиционные методы оценивая коэффициентов и довольно таки легки в использовании. Косвенный МНК применим для оценивания структурных параметров отдельного уравнения системы и может дать результат, если уравнение полностью идентифицируемо. [7, c.353], а двухшаговый МНК используется для оценки параметров сверхидентифицируемого уравнения.

Метод максимального правдоподобия рассматривается как более обобщенный метод оценивания параметров, результаты которого при нормальном распределении признаков совпадает с МНК. Однако при большом количестве уравнений в модели данной способ может привести к сложным вычислениям. Поэтому в качестве новшества используют метод максимального правдоподобия с ограниченной информацией, разработанный в 1949 г., T.Andersen и N.Rubin, помимо этого, данный метод использовал в своих работах D.Dzhoston. Отличием данного метода от метода максимального правдоподобия является то, что в данном методы сняты все ограничения на параметры, связанные с функционированием системы в целом. Это делает решение достаточно простым, но объем трудоемкости сохранена. Несмотря на его популярность в 60 –е годы он был вытеснен двухшаговым МНК, так как он был очень прост в использовании. Этому конечно же способствовала работа от 1961 г G.Tail о семействе оценок коэффициентов структурной модели. В своей работе G.Tail определил семейство оценок класса K и явным образом показал, что он включает в себя три важных оператора оценивания: при K = 0 – это обычный МНК, при K = 1 – ДМНК и при plim K = 1 – метод ограниченной информации. В последнем случае решение структурной модели соответствует результатам оценивания по ДМНК.

Дальнейшее развитие ДМНК привело к разработке трехшагового МНК (ТМНК). Данный метод является, своего рода, обобщением всех предыдущих способов оценивания и он пригоден для всех для всех видов уравнений структурной модели. Но при наложении ограничений на параметры более эффективным оказывается ДМНК. Данный метод был разработан в совместной работе A.Zelner и G.Tail в 1962 году.

Некоторые, самые актуальные методы изучим подробней.

Косвенный метод наименьших квадратов (КМНК)

Остановимся подробней на косвенном методе наименьших квадратов. Для начала рассмотрим систему одновременных уравнений:

(1.1.5)

Главной причиной того, что к данной системе мы не можем применить обычный метод наименьших квадратов, является то, что эндогенные переменные коррелируют со случайными ошибками, поэтому данную систему необходимо разрешить относительно Y так, чтобы в правой части остались только экзогенные переменные Х. Для уравнения (1.1.5) это можно сделать, а затем к полученным уравнениям применить МНК и тем самым получить оценки некоторых выражений от исходных параметров. Такая процедура называется косвенным методом наименьших квадратов. Применим данный метод к уравнению (1.1.5). Для начала запишем уравнение в виде:

(1.1.6)

где

(1.1.7)

Для простоты счета будет считать, что a = 0, то есть переменные Y отцентрированы (в практическом применении метода это не особо важно). К системе (1.1.6) применим МНК и тем самым получим оценки параметров b и c.

где ,,

–значение переменных

Тем временем из равенства (1.1.7) однозначно можно выразить исходные параметры черезa,b,c:

(1.1.8)

Таким образом, используя (1.1.7) получаем:

Оценки (1.1.8) являются оценками косвенного МНК. [8, с.228] Главным отличием оценок косвенного МНК от обычного МНК является то, что они состоятельные.

Двухшаговый метод наименьших квадратов (ДМНК)

Для сверхидентифицируемой системы применение КМНК не дает однозначной оценки параметров структурной модели. В этом случае получают применение другие методы. Самым используемым для сверхидентифицируемой системы является двухшаговый МНК. Основная цель двухшагового МНК – получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащиеся в правой части, используя приведенную форму модели. Затем, полученные значения можно подставить вместо фактических значений и применить обычный МНК к структурной форме. Данный метод получил свое название потому, что МНК применяется дважды. Двухшаговый МНК является наиболее общим и при применении его для точно идентифицируемых уравнений его результаты совпадают с косвенным МНК. Также ДМНК используется в компьютерных программах, например, в DSTAT.

Несмотря на всю важность систем эконометрических уравнений, чаще всего на практике часто на практике не учитываются некоторые нюансы. Конечно, все методы нам известны, изучены, но обычно при нахождении решения систем одновременных уравнений, построении производственных функций используют обычный, либо косвенный МНК. [5, с 200]