4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение
(16)
где
коэффициенты
– постоянные, называетсялинейным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Если
,
то уравнение (16) называетсянеоднородным.
Если
,
то уравнение (16) называетсяоднородным.
I. Рассмотрим однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
(17)
Общим решением уравнения (17) является функция
(18)
где
– фундаментальная система решений
уравнения (17).
Фундаментальной системой решений называется всякая система линейно независимых решений, содержащая столько функций, каков порядок дифференциального уравнения.
Функции
называютсялинейно
зависимыми
в интервале
,
если существуют постоянные числа
,
не все равные нулю, такие что
для любых
.
Если же указанное тождество выполняется
только в случае, когда
и
,
то функции
называютсялинейно
независимыми
в интервале
.
Кратко
критерий линейной независимостиможет быть сформулирован следующим
образом: функции
являются линейно независимыми, если
определитель Вронского
отличен
от нуля. В противном случае функции
линейно зависимы.
Алгоритм нахождения общего решения однородного уравнения (17):
1)
составляют соответствующее ему
характеристическое уравнение (заменяя
в однородном уравнении производные от
искомой функции на k
в соответствующей степени, то есть
на
,
на
и
на
)
(18).
Полученное
квадратное уравнение может иметь (в
зависимости от дискриминанта
)
два различных действительных решения,
два совпадающих (кратный корень)
действительных решения и пару
комплексно-сопряженных решений;
2) в зависимости от корней характеристического уравнения выделяются частные решения (соответствующие корням характеристического уравнения), образующие фундаментальную систему решений и записывается соответствующее общее решение (18).
|
|
Корни характеристического уравнения |
Частные решения |
Общее решение однородного дифференциального уравнения |
|
I |
Два
действительных и различных корня,
т.е.
|
|
|
|
II |
Два
действительных и совпадающих корня,
т.е.
|
|
|
|
III
|
Два
комплексно сопряженных решения, т.е.
|
|
|
,
Пример. Найти общее решение дифференциального уравнения
a)
,
b)
,
c)
.
Решение.Во всех трех случаях имеем однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Общее решение найдем по приведенному выше алгоритму.
Пример
a.
.
Составим характеристическое уравнение
и решим его
;
;
.
Характеристическое уравнение имеет два различных действительных решения, т.е. имеем первый случай. В соответствии с приведенной таблицей можно выписать фундаментальную систему решений данного уравнения
,
и получить общее решение исходного дифференциального уравнения
.
Сделаем проверку найденного общего решения. Для этого найдем первую и вторую производную от общего решения
,
,
.
Подставим общее решение вместе с найденными производными в исходное уравнение
Пример
b.
.
Составим характеристическое уравнение
.
Не сложно заметить, что в правой части уравнения записан полный квадрат разности
.
Откуда
получим
(аналогичный результат можно было
получить, используя обычный метод
решения квадратных уравнений).
Характеристическое уравнение имеет два совпадающих действительных решения (или один действительный корень кратности два), т.е. имеем второй случай. В соответствии с приведенной таблицей можно выписать фундаментальную систему решений данного уравнения
,
и получить общее решение исходного дифференциального уравнения
.
Пример
c.
.
Составим характеристическое уравнение
и решим его
;
;
.
Характеристическое уравнение имеет два комплексно сопряженных решения, т.е. имеем третий случай. В соответствии с приведенной таблицей можно выписать фундаментальную систему решений данного уравнения
, 
и получить общее решение исходного дифференциального уравнения
.
II. Рассмотрим теперь решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами (16):
.
В общем случае это уравнение может быть решено методом вариации произвольных постоянных (методом Лагранжа). Алгоритм нахождения решения методом Лагранжа состоит в следующем:
1. Находим общее решение однородного линейного уравнения (17), соответствующего исходному неоднородному уравнению (16)
.
2. Будем искать общее решение неоднородного уравнения в виде общего решения однородного уравнения, считая, что произвольные постоянные являются функциями независимой переменной x, т.е. в виде
.
При
этом функции
могут быть найдены как решения системы
которая
является линейной системой двух
алгебраических уравнений с двумя
неизвестными относительно
.
Определитель этой системы является
определителем Вронского, который отличен
от нуля, если
образуют фундаментальную систему
решений. Поэтому система двух алгебраических
уравнений с двумя неизвестными имеет
единственное решение
.
Интегрируя полученные равенства, найдем
функции
и тем самым получим общее решение
исходного неоднородного уравнения.
Метод вариации произвольных постоянных достаточно сложен, поэтому в ряде случаев, когда правая часть имеет специальный вид, можно использовать другой метод – метод неопределенных коэффициентов, воспользовавшись следующим утверждением о структуре общего решения неоднородного обыкновенного дифференциального уравнения.
Общее
решение
линейного неоднородного дифференциального
уравнения (16) равно сумме общего решения
соответствующего однородного уравнения
(17) и частного решения
исходного неоднородного уравнения
(16), т.е.
.
Общее
решение
линейного однородного уравнения находим
по алгоритму, приведенному выше. Далее
необходимо найти частное решение
неоднородного уравнения. В некоторых
случаях вид частного решения устанавливается
по правой части исходного неоднородного
уравнения.
Если правая часть дифференциального уравнения имеет вид
где
– многочлены степениn
и m
соответственно, а
и b –
некоторые постоянные числа, то частное
решение неоднородного уравнения будет
иметь следующую структуру:
где
– многочлены степени
,
записанные с неопределенными
коэффициентами;r
– равно числу корней характеристического
уравнения (18), совпадающему с числом
.
Таким образом,
,
если среди корней характеристического
уравнения
нет числа
;
,
если существует один корень
характеристического уравнения
или
,
совпадающий с числом
;
,
если существует двукратный корень
характеристического уравнения,
совпадающий с числом
.
Зная структуру частного решения неоднородного уравнения, неизвестными которого являются только коэффициенты многочленов, подставим его вместе с производными в исходное уравнение и, приравнивая коэффициенты подобных членов слева и справа, получаем необходимое количество линейных алгебраических уравнений для вычисления этих неизвестных коэффициентов.
Таким образом, для правой части специального вида общее решение дифференциального уравнения может быть легко найдено с помощью элементарных операций, таких как дифференцирование и решение линейных алгебраических уравнений, не прибегая к операции интегрирования, которая необходима в методе вариации произвольных постоянных.
Частными случаями правой части специального вида дифференциального уравнения являются следующие:
,
которая получается из общего случая
при
;
,
которая получается из общего случая
при
;
,
которая получается из общего случая
при
.
В заданиях 4 и 5 необходимо найти общие решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами, в которых правая часть имеет специальный вид. Эти задания можно решать как методом вариации произвольных постоянных (методом Лагранжа), так и методом неопределенных коэффициентов. По нашему мнению, последний метод предпочтительнее, так как в нем не требуется применять операцию интегрирования. При решении задания 4 будут показаны оба метода. В задании 5 будет проиллюстрирован только один метод – метод неопределенных коэффициентов.
Задание 4. Найти общее решение дифференциального уравнения.
Сделать проверку.
Решение. Имеем обыкновенное дифференциальное уравнением второго порядка с постоянными коэффициентами. Решим данное уравнение двумя способами: первый способ – метод неопределенных коэффициентов (правая часть специального вида); второй способ – метод вариации произвольных постоянных.
√Первый
способ.
Общее решение
исходного линейного неоднородного
дифференциального уравнения имеет
вид:
.
где
– общее решение соответствующего
однородного уравнения,
–частное
решение исходного неоднородного
уравнения.
а)
Найдем
– общее решение соответствующего
однородного уравнения, т.е. уравнения
.
Для
этого составим характеристическое
уравнение, заменив в нем
на
,
на
и
на
:
Решая
квадратное уравнение, получим корни
характеристического уравнения
,
.
Эти корни являются действительными и
различными, поэтому фундаментальная
система решений, соответствующая этим
корням, будет иметь вид
,
.
Следовательно, общее решение однородного
уравнения определяется формулой:
.
б)
Найдем
– частное решение исходного неоднородного
уравнения. Для этого рассмотрим правую
часть исходного неоднородного уравнения
.
Правая
часть исходного уравнения будет иметь
специальный вид, если
,
,
,
т.е.
,
,
т.е.
.
Так как правая часть имеет специальный
вид, структура частного решения в общем
случае будет иметь вид:
.
Так
как
и число
,
то
.
Так как
и
,
то
,
т.е.
,
.
Тогда структура частного решение
исходного неоднородного уравнения с
неопределенными коэффициентами будет
иметь вид:
,
,
.
Коэффициенты A и B определим методом неопределенных коэффициентов. Для этого найдем первую и вторую производные от частного решения
,
Подставим найденные выражения в исходное уравнение:
Разделим
обе части на
и приравняем коэффициенты при одинаковых
степенях переменной, т.е. при
,
и
.
Получим систему, из которой найдем
коэффициенты
и
.
Таким образом,
или
Решая
систему двух линейных алгебраических
уравнений с двумя переменными, получим
,
.
Тогда частное решение
.
Общее решение исходного неоднородного уравнения определяется формулой
Таким
образом,
Сделаем проверку.
,
Подставим
,
,
в исходное уравнение
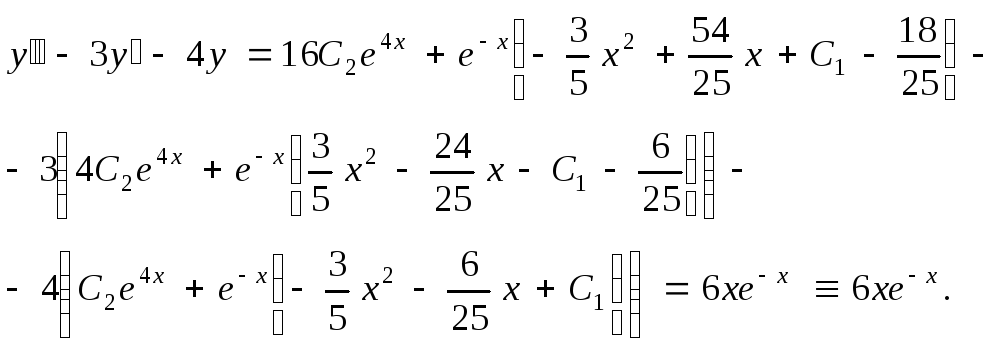
Получили верное равенство.
√Второй способ a) Запишем общее решение соответствующего однородного дифференциального уравнения (как это было сделано в первом способе в пункте a):
.
б) Будем искать общее решение неоднородного линейного уравнения в виде общего решения однородного линейного уравнения, считая, что произвольные постоянные являются функциями независимой переменной x, т.е. в виде
.
Функции
могут быть найдены из решения системы
где
,
,
,
,
,
т.е.
,
.
Таким образом,
,
.
Тогда
Обозначив
через
,
окончательно получим
Ответ:
общее решение
Задание 5. Найти общее решение (общий интеграл) дифференциального уравнения. Сделать проверку.
.
Решение. Данное уравнение является обыкновенным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Его
общее решение
имеет вид:
.
где
– общее решение соответствующего
однородного уравнения,
–частное
решение исходного неоднородного
уравнения.
а).
Найдем
– общее решение соответствующего
однородного уравнения, т.е. уравнения
.
Для
этого составим характеристическое
уравнение, заменив в нем
на
,
на
и
на
:
.
Решая
квадратное уравнение (
,
,
),
найдем корни характеристического
уравнения
,
т.е.
и
.
Имеем два комплексно-сопряженных корня
(третий случай), поэтому фундаментальная
система решений, соответствующая этим
корням, будет иметь вид:
,
.
Следовательно, общее решение однородного
уравнения определяется формулой:
.
б)
Найдем
– частное решение исходного неоднородного
уравнения. Для этого рассмотрим правую
часть исходного неоднородного уравнения
.
Правая
часть исходного уравнения будет иметь
специальный вид, если
,
,
,
т.е.
,
,
т.е.
.
Так как правая часть имеет специальный
вид, то структура частного решения в
общем случае будет иметь вид:
.
,
т.е.
,
.
Тогда структура частного решение исходного неоднородного уравнения с неопределенными коэффициентами будет иметь вид:
,
.
Коэффициенты A и B определим методом неопределенных коэффициентов. Для этого подставим частное решение с неопределенными коэффициентами в исходное уравнение, предварительно вычислив первую и вторую производные
.
Тогда
Таким образом,
Разделим
обе части равенства на
и приравняем коэффициенты при
и
.
Получим систему, из которой найдем
коэффициенты
и
.
Таким образом,
или
Тогда частное решение
.
Общее решение исходного неоднородного уравнения определяется формулой
Таким
образом,
Проверка выполняется аналогично тому, как это было показано в задании 4.