МАТЕМАТИКА (ІДЗ) / Rozdil1_21

Розв’язуючи систему, одержимо чотири стаціонарні точки:

Знайдемо похідні другого порядку

і складемо дискримінант

для кожної стаціонарної точки:

1. Для точки

   Отже, в точці екстремумів немає.

2. Для точки В точці функція має мінімум:

3. Для точки Екстремумів немає.

4. Для точки В точці функція має максимум, який дорівнює

2. Знайти найбільше та найменше значення функції в області , обмеженій прямими та параболою при (рис.1.23 )

Рис.1.23

Знайдемо критичні точки, які лежать всередині області . Для цього обчислимо частинні похідні: Розв’язавши систему рівнянь 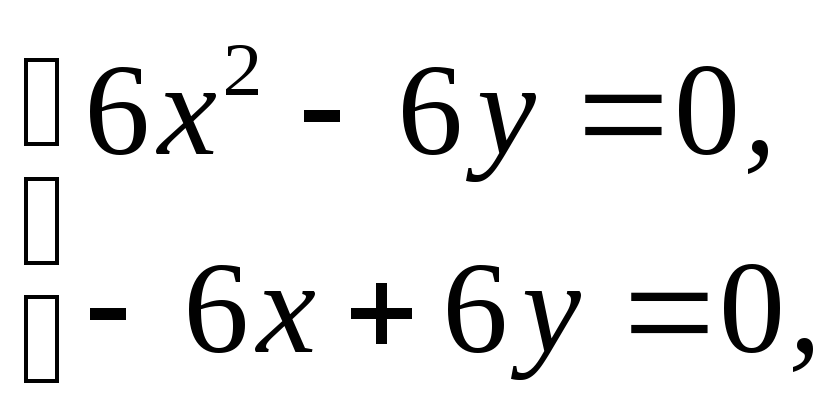знайдемо дві критичні точки: і Точка належить границі області . Тому, якщо функція набуває найбільше (найменше) значення у внутрішній точці області, то цією точкою може бути тільки .

Дослідимо функцію на границі області. На відрізку , отже, Функція є зростаючою функцією однієї змінної на відрізку , найбільше і найменше значення вона набуває на кінцях відрізка .

На відрізку , тому тут функція є функцією однієї змінної . Її глобальні екстремуми містяться серед її значень в критичних точках і на кінцях відрізка. Знаходимо частинну похідну . Розв’язуємо рівняння звідки . Всередині відрізка є лише одна критична точка , на відрізку їй відповідає точка .

Отже, глобальні екстремуми на відрізку функція може мати в точках і .

На дузі параболи маємо

Розв’язуючи рівняння знаходимо критичні точки і

Отже, найбільше і найменше значення функціїї в даній замкненій області знаходяться серед її значень в точках :

звідки .

3. Розв’язати задачу.

Із листа жерсті площею треба виготовити закриту коробку у формі паралелепіпеда, яка мала би найбільший об’єм.

Задача зводиться до відшукання максимума функції де - відповідно довжина, ширина і висота коробки, при умові

Складемо функцію Лагранжа:

Знайдемо частинні похідні Прирівнявши їх до нуля, одержимо систему рівнянь:

Розв’язавши одержану систему, знайдемо координати єдиної стаціонарної точки :

Із змісту задачі зрозуміло, що вказана точка є точкою умовного максимума: об’єм коробки не може бути необмежено великим. Отже, природньо вважати, що при даних значеннях довжин сторін цей об’єм буде найбільшим.

Таким чином, закрита коробка з максимальним об’ємом, яку можна виготовити із листа жерсті площею , повинна мати форму куба зі

стороною .

268