МАТЕМАТИКА (ІДЗ) / Rozdil1_21
.doc-
ЕКСТРЕМУМИ ФУНКЦІЇ КІЛЬКОХ ЗМІННИХ
-
Екстремум функції. Функція
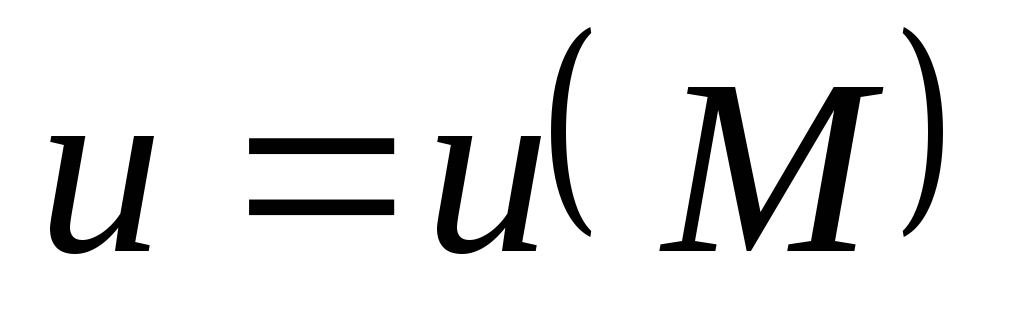має
максимум
(мінімум)
в точці
якщо існує такий окіл точки
що
для всіх точок
які
відмінні від точки
виконується
нерівність
(відповідно
).
Максимум або мінімум функції називається її екстремумом.
Необхідна
умова екстремума (функції двох змінних).
Якщо диференційовна функція
досягає екстремума в точці
то в цій точці
Точки,
в яких частинні похідні
дорівнюють нулю, називаються стаціонарними
точками функції
.
Таким чином, якщо
точка екстремума, то
стаціонарна
точка або в цій точці функція
недиференційовна.
Достатні
умови екстремума (функції двох змінних).
Нехай
стаціонарна
точка функції
,
причому ця функція
двічі диференційовна в деякому околі
точки
і всі її частинні похідні 2-го порядку
неперервні в точці
.
Введемо позначення:
Тоді:
-
якщо
,
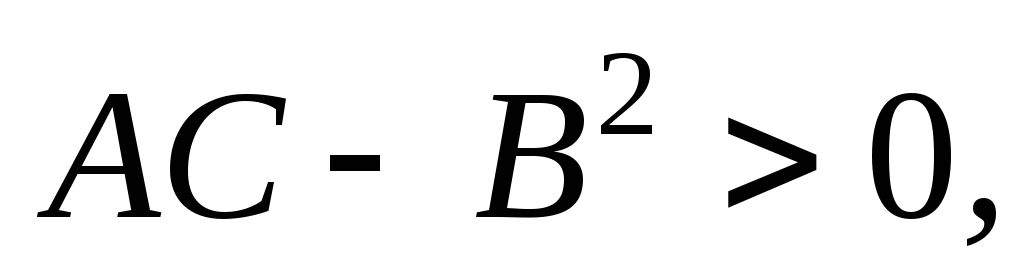
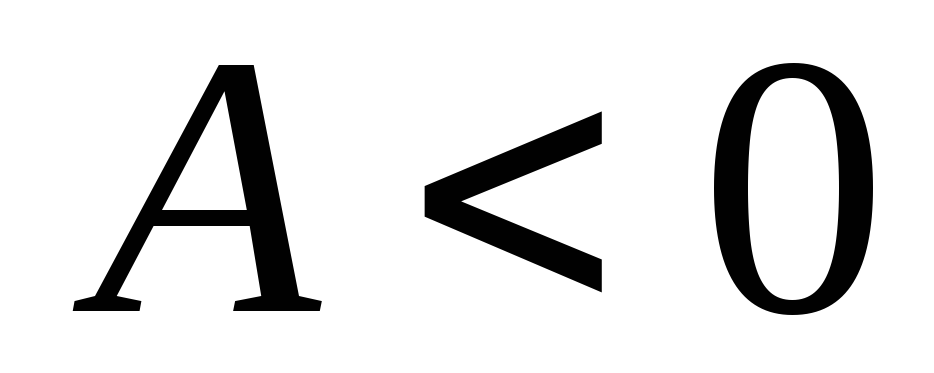то функція
має
в точці
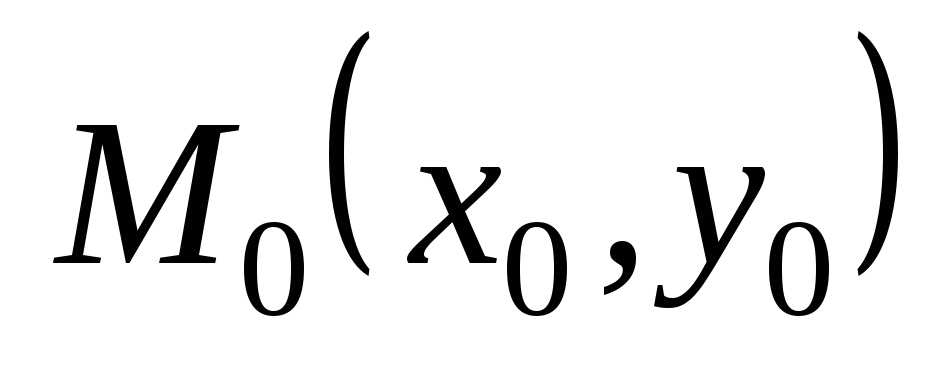максимум;
2) якщо
,
то функція
має в
точці
мінімум;
3) якщо
то функція
в точці
екстремума не має;
4) якщо
то потрібне додаткове дослідження.
Якщо
функція
диференційовна в обмеженій замкнутій
області, то вона досягає свого найменшого
(найбільшого) значень або в стаціонарних
точках, або на границі області.
2.
Умовний екстремум. Нехай
потрібно знайти максимум (мінімум)
функції
змінних
при умові, що змінні
зв’язані
рівняннями
Задача
знаходження умовного екстремума
зводиться до дослідження на звичайний
екстремум функції Лагранжа
Прирівнюючи
до нуля її частинні похідні по змінних
і множниках
із системи
рівнянь
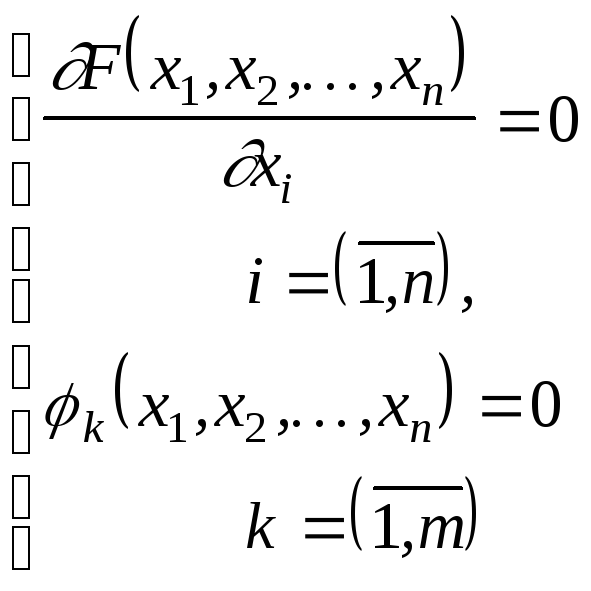(1.54)
визначаємо
і допоміжні множники
Необхідні умови умовного екстремуму
дають можливість визначити координати
точки
,
в якій можливий умовний екстремум.
Необхідні додаткові дослідження характеру критичної точки. При розв’язуванні конкретних задач інколи вдається встановити характер
критичної точки, виходячи із самої суті задачі.
АР-1.21
1. Знайти стаціонарні
точки функції
і дослідити їх характер. (Відповідь: в
точці
немає екстремума. В точці
- мінімум).
2. Знайти найбільше
значення функції
в трикутнику, обмеженому прямими
.
(Відповідь:
найбільше значеня
в стаціонарній точці
(ця точка є, таким чином, точкою максимума).
Найменше значення
в
точці
- на межі).
3. Дослідити на
екстремум функцію
при
.
(Відповідь:
або
(максимум),
або
(мінімум)).
4. Намет має форму
циліндра з насадженою на нього конічною
верхівкою. При яких співвідношеннях
між лінійними вимірами намета для його
виготовлення буде потрібно найменшу
кількість матеріалу при заданому об’ємі
? (Відповідь: якщо
-
радіус намета,
-
висота циліндричної частини,
-
висота конічної верхівки, то:
).
5. На
параболі
знайти точку, найближчу до прямої
.
(Відповідь:
).
СР-1.21
Дослідити на екстремуми функцію:
-
(Відповідь:
). -
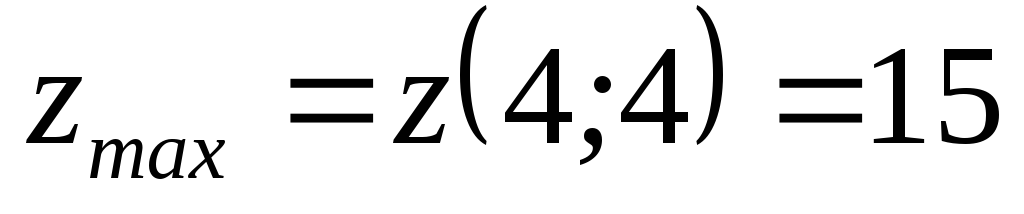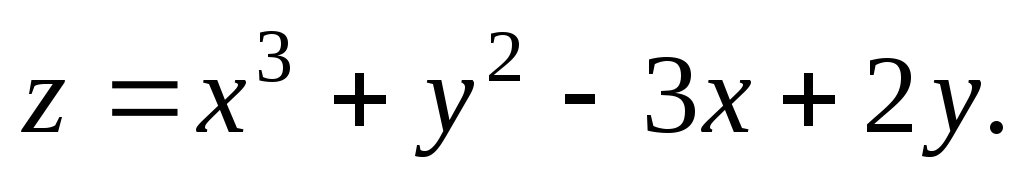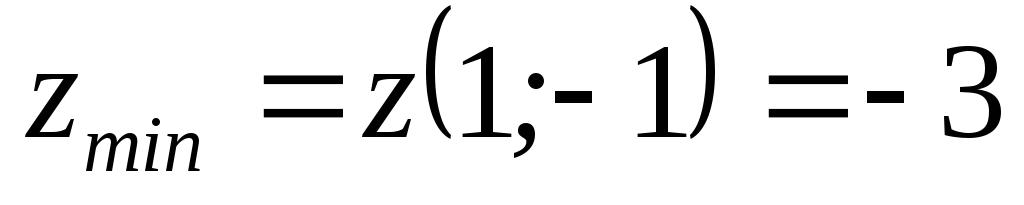(Відповідь:
). -
(Відповідь:
).
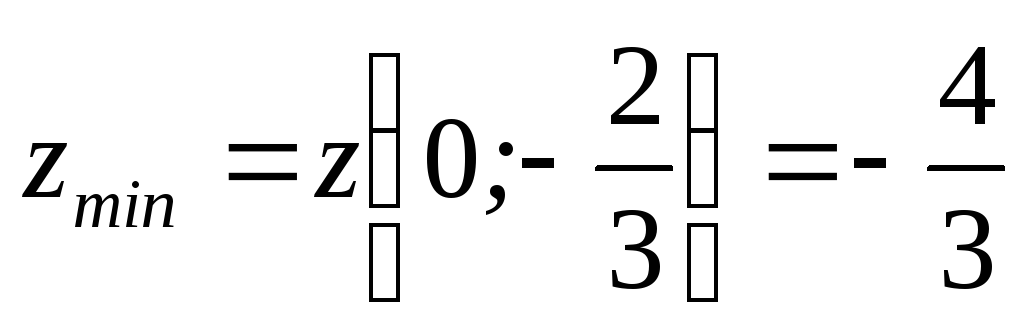ІДЗ-1.21
1. Дослідити на екстремуми дані функції:
1.1
(Відповідь:
).
1.2.
(Відповідь:
).
1.3.
(Відповідь:
).
1.4.
(Відповідь:
).
1.5.
(Відповідь:
).
1.6.
(Відповідь:
).
1.7.
(Відповідь:
).
1.8.
(Відповідь:
).
1.9.
(Відповідь:
)
1.10.
(Відповідь:
).
1.11.
(Відповідь:
).
1.12.
(Відповідь:
).
1.13.
(Відповідь:
).
1.14.
(Відповідь:
).
1.15.
(Відповідь:
).
1.16.
(Відповідь:
).
1.17.
(Відповідь:
).
1.18.
(Відповідь:
).
1.19.
(Відповідь:
).
1.20.
(Відповідь:
).
1.21.
(Відповідь:
).
1.22.
(Відповідь:
).
1.23.
(Відповідь:
).
1.24.
(Відповідь:
).
1.25.
(Відповідь:
).
1.26.
(Відповідь:
).
1.27.
(Відповідь:
).
1.28.
(Відповідь:
).
1.29.
(Відповідь:
).
1.30.
(Відповідь:
).
2. Знайти
найбільше та найменше значення функції
в
області
,
обмеженій заданими лініями:
2.1.
(Відповідь:
).
2.2.
(Відповідь:
).
2.3.
(Відповідь:
).
2.4.
(Відповідь:
).
2.5.
(Відповідь:
).
2.6.
(Відповідь:
).
2.7.
(Відповідь:
).
2.8.
(Відповідь:
).
2.9.
(Відповідь:
).
2.10.
(Відповідь:
).
2.11.
(Відповідь:
).
2.12.
(Відповідь:
).
2.13.
(Відповідь:
).
2.14.
(Відповідь:
).
2.15.
(Відповідь:
).
2.16.
(Відповідь:
).
2.17.
(Відповідь:
).
2.18.
(Відповідь:
).
2.19.
(Відповідь:
).
2.20.
(Відповідь:
).
2.21.
(Відповідь:
).
2.22.
(Відповідь:
).
2.23.
(Відповідь:
).
2.24.
(Відповідь:
).
2.25.
(Відповідь:
).
2.26.
(Відповідь:
).
2.27.
(Відповідь:
).
2.28.
(Відповідь:
).
2.29.
(Відповідь:
).
2.30.
( Відповідь:
).
3. Розв’язати задачі:
3.1.
Знайти прямокутний паралелепіпед з
найменшою поверхнею при умові, що його
об’єм
дорівнює
.
(Відповідь: куб).
3.2.
Знайти сторони трикутника з даним
периметром
,
який при обертанні навколо однієї із
своїх сторін утворює тіло з найбільшим
об’ємом.
(Відповідь:
).
3.3. На
еліпсі
дано дві точки
і
.
Знайти на цьому еліпсі третю точку
таку,
щоб трикутник
мав найбільшу площу.
(Відповідь:
).
3.4.
Знайти прямокутний паралелепіпед з
даною поверхнею
,
який мав би найбільший об’єм.
(Відповідь: куб).
3.5.
Знайти об’єм
найбільшого прямокутного паралелепіпеда,
який можна вписати в еліпсоїд з півосями
і
.
(Відповідь:
).
-
Переріз канала має форму рівнобічної трапеції з даною площею. Як вибрати його виміри, щоб поверхня канала, яка обмивається
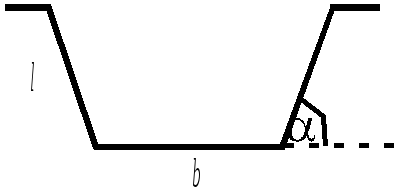
Рис.1.22
водою, була найменшою (рис.1.22 )?
(Відповідь:
де
-
дана площа перерізу. При цьому поверхня,
що обмивається , дорівнює
).
3.7. Із всіх прямокутних паралелепіпедів, що мають дану діагональ, знайти такий, об’єм якого був би найбільшим. (Відповідь: куб).
3.8.
Навколо даного еліпса описати трикутник
з основою, паралельною до більшої осі,
площа якого була би найменшою. (Відповідь:
найменша площа дорівнює
).
3.9.
Знайти найбільший об’єм
паралелепіпеда при умові, що сума всіх
його ребер дорівнює
.
(Відповідь:
(куб)).
3.10. На
параболі
знайти точку, найменш віддалену від
прямої
.
(Відповідь:
).
3.11.
Знайти сторони прямокутного трикутника
з даною площею
,
який мав би найменший периметр. (Відповідь:
і
).
-
Знайти правильну трикутну піраміду з даним об’ємом
,
яка мала би найменшу суму ребер. (Відповідь: тетраедр).
3.13. На
еліпсі
знайти точки, які лежали б на найменшій
та найбільшій відстані від прямої
.
(Відповідь:
і
).
3.14.
Знайти найбільшу відстань точок поверхні
від площини
.
(Відповідь:
).
3.15. На
еліпсоїді обертання
знайти точки, які були б найменш та
найбільш віддалені від площини
.
(Відповідь:
).
3.16. На
параболі
знайти точку, найближчу до прямої
.
(Відповідь:
).
3.17. В
еліпсоїд вписати прямокутний паралелепіпед
з найбільшим об’ємом.
(Відповідь: виміри паралелепіпеда
де
і
-
півосі еліпсоїда).
3.18. Із всіх трикутників, вписанинх в круг , знайти такий, у якого площа була б найбільшою. (Відповідь: рівносторонній).
3.19. Із
всіх прямокутників, які мають задану
площу
,
знайти такий, периметр якого мав би
найменше значення. (Відповідь: квадрат,
).
-
Знайти виміри прямокутного паралелепіпеда, який мав би при даній повній поверхні
максимальний об’єм.
(Відповідь:
куб,
).
3.21. При
яких вимірах відкрита прямокутна ванна
з даною ємкістю
має
найменшу поверхню? (Відповідь:
).
3.22.
Через точку
провести площину, яка утворила би з
координатними площинами тетраедр з найменшим об’ємом.
(Відповідь:
).
3.23. Із
всіх прямокутних трикутників з даною
площею
знайти
такий, гіпотенуза якого має найменше
значення.
(Відповідь: рівнобедрений.)
3.24.
Знайти прямокутний паралелепіпед, який
мав би найбільший об’єм
при даній повній поверхні
.
(Відповідь: куб
з ребром
).
3.25.На
площині
знайти точку, сума квадратів відстаней
якої до точок
і
була би найменшою.
(Відповідь:
).
3.26. Дано
точки
На поверхні сфери
знайти таку точку
,
щоб об’єм
піраміди
був: а) найбільшим, б) найменшим.
(Відповідь:
а)
б)
).
3.27. В
прямий еліптичний конус, півосі основи
якого дорівнюють
і
,
висота
,
вписана призма з прямокутною основою
так, що сторони основи паралельні осям,
а перетин діагоналей основи лежить в
центрі еліпса. Якими повинні бути сторони
основи і висота цієї призми, щоб її об’єм
був найбільшим? Знайти цей найбільший
об’єм.
(Відповідь:
Висота
,
сторони основи
і
об’єм
).
3.28.
Знайти виміри циліндра з найбільшим
об’ємом
при умові, що його повна поверхня дорівнює
.
(Відповідь:
м,
м).
3.29.
Подати додатне число
у вигяді добутку чотирьох додатних
множників так, щоб їх сума була найменшою.
(Відповідь:
).
3.30.
Визначити розміри конуса з найбільшим
об’ємом
при умові, що його бічна поверхня
дорівнює
.
(Відповідь:
).
РОЗВ’ЯЗОК ТИПОВОГО ВАРІАНТА
1. Дослідити на екстремуми функцію
Знайдемо частинні похідні і складемо систему рівнянь:
або