7

Лекция 7

Вычисление определённых интегралов

Для функции вида y=f(x) значением интеграла в пределах [a, b] при условии, что на этом интервале f(x)>0, является площадь под кривой f(x), ограниченная вертикальными прямыми x=a и x=b (рис. 1).

Рис. 1. Графическая интерпретация определённого интеграла.

Все численные методы решения задач, связанных с вычислением определённых интегралов, основаны на графической интерпретации данной задачи. Иными словами, вычислить определённый интеграл одним из численных методов, значит найти площадь под кривой, образованной подынтегральной функцией, в заданных пределах интегрирования.

Общеизвестно, что аналитически определённый интеграл вычисляется с использованием первообразных:

. (1)

Однако первообразные известны или достаточно легко выводятся для простых функций. Для функционалов со сложными структурами приходится прибегать к численным методам.

Среди методов численного интегрирования рассмотрим методы прямоугольников, трапеций и парабол (Симпсона).

Метод прямоугольников, как и все другие методы, основан на разбиении исходного интервала интегрирования [a, b] на равные, малые по величине подынтервалы, на которых рассчитывается площадь простейшей геометрической фигуры, в данном случае – прямоугольника.

Шаг интегрирования (ширина подынтервала) (x) напрямую зависит от количества подынтервалов (n):

. (2)

Графическая иллюстрация метода прямоугольников представлена на рис. 2.

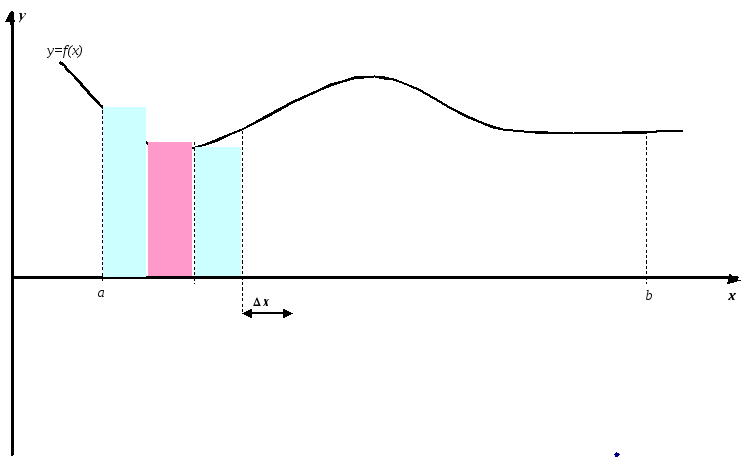
Рис. 2. Графическая иллюстрация метода прямоугольников.

Алгоритм метода прямоугольников следующий.

1. Выбирается шаг интегрирования (количество подынтервалов).

2. По соотношению (3) рассчитывается сумма площадей на всех подынтервалах:

, (3)

где здесь и далее .

Задание 1. Для функции вида вычислить определённый интеграл в пределах [–2; 2] двумя способами: аналитически и методом прямоугольников при n=8. Рассчитать погрешности численного метода.

Аналитическое решение:

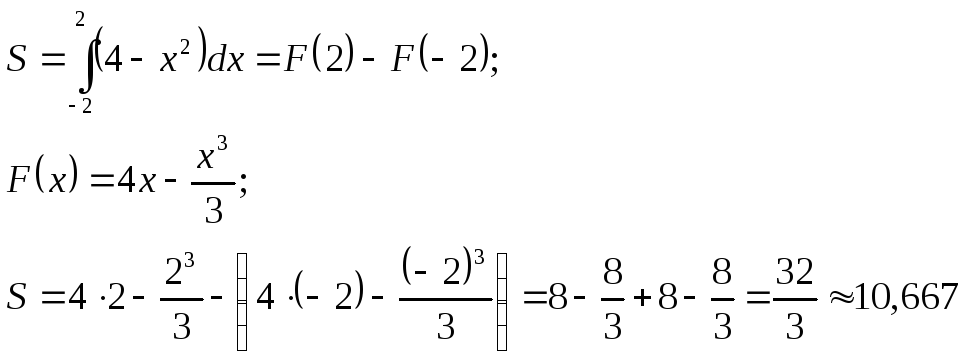
Численное решение представлено в табл. 1.

Таблица 1

Вычисление определённого интеграла методом прямоугольников

xi	f(xi)	f(xi)x
–2,0	0,00	0,000
–1,5	1,75	0,875
–1,0	3,00	1,500
–0,5	3,75	1,875
0,0	4,00	2,000
0,5	3,75	1,875
1,0	3,00	1,500
1,5	1,75	0,875
f(xi)x		10,5

Абсолютная погрешность метода: |10,500–10,667|=0,167.

Относительная погрешность: .

Очевидно, что чем меньше шаг интегрирования, тем меньшую погрешность даёт метод. Однако в данной постановке погрешность всё равно будет достаточно высокой. Для уменьшения ошибки можно модифицировать метод прямоугольников.

Модификация метода прямоугольников заключается в том, что высота прямоугольника на каждом участке интегрирования определяется не значением функции в крайней точке участка, а значением функции, вычисленном в середине подынтервала (рис. 3).

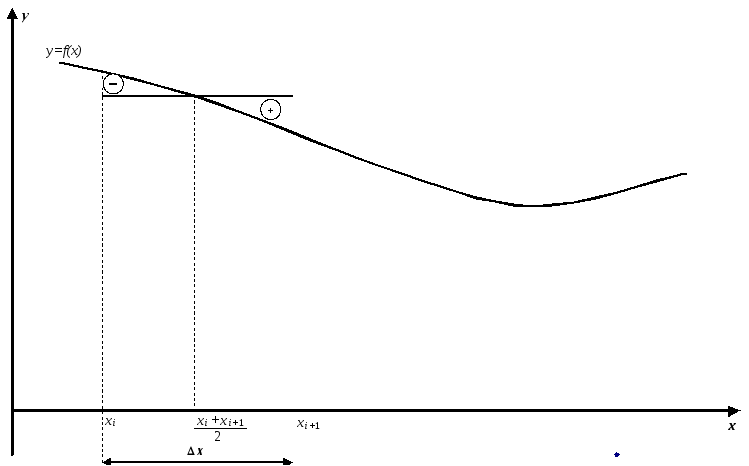
Рис. 3. Графическая иллюстрация модификации метода прямоугольников.

В этом случае в алгоритме формула (3) изменяется:

. (4)

Задание 2. Для функции вида вычислить определённый интеграл в пределах [–2; 2] модифицированным методом прямоугольников. Рассчитать погрешности данного метода.

Численное решение представлено в табл. 2.

Таблица 2

Вычисление определённого интеграла модифицированным методом прямоугольников

xi+0,5x	f(xi+0,5x)	f(xi+0,5x)x
–1,75	0,9375	0,46875
–1,25	2,4375	1,21875
–0,75	3,4375	1,71875
–0,25	3,9375	1,96875
0,25	3,9375	1,96875
0,75	3,4375	1,71875
1,25	2,4375	1,21875
1,75	0,9375	0,46875
f(xi+0,5x)x		10,75

Абсолютная погрешность метода: |10,750–10,667|=0,083.

Относительная погрешность: .

В методе трапеций, как следует из названия, формой каждого участка под заданной кривой является не прямоугольник, а трапеция (рис. 4). Соответственно, и площадь каждого участка вычисляется по формуле площади трапеции.

Формула для вычисления определённого интеграла выглядит следующим образом:

. (5)

Задание 3. Для функции вида вычислить определённый интеграл в пределах [–2; 2] методом трапеций. Рассчитать погрешности данного метода.

Численное решение представлено в табл. 3.

Таблица 3