Построение регрессионной прямой по сгруппированным данным

При большом числе наблюдений обычно производят группировку данных по одной или нескольким переменным. Для исследования зависимостей желательно использовать равные по ширине интервалы группировок. Неравные интервалы могут привести к искажению регрессии и ошибочным выводам. При большом объеме изучаемой совокупности наиболее целесообразно образовывать 9 – 10 интервалов, равномерно заполненных частотами. При небольших объемах совокупности нет смысла производить группировку данных. Оценки, вычисленные по сгруппированному материалу, отличаются от оценок, вычисленных по несгруппированному материалу. Причина этого – в переходе при расчетах к серединам интервалов и условно принятому равномерному распределению частот по ширине этих интервалов. При большом объеме данных считается, что неточности в результатах за счет группировки вполне искупаются упрощением процедуры вычисления.

Тема 3. Модель множественной линейной регрессии

1. Определение параметров модели парной линейной регрессии методом наименьших квадратов

2. Оценка тесноты связи между переменными

3. Оценка качества уравнения регрессии

4. Предпосылки метода наименьших квадратов

Линейная множественная регрессия

В действительности каждое явление определяется действием не одной причины, а нескольких, а точнее целым комплексом причин. Сложное сочетание причин приводит к различным результатам. Например, действуя в одном и том же направлении, они усиливают действие, действуя в противоположном направлении – ослабляют друг друга. Возникает вопрос об измерении воздействия комплекса причин на изучаемое явление. Задача изучения зависимости одной зависимой переменной от нескольких объясняющих переменных x₁, x₂, …, x_mв условиях конкретного времени решается с помощью множественного или многофакторного регрессионного анализа. Рассмотрим линейное соотношение между переменнойyи объясняющими переменнымиx₁, x₂, …, x_m.

Коэффициенты b_k,k= 0, 1, 2, …,mназываются параметрами регрессии. Постоянная регрессииb₀выполняет в уравнении регрессии функцию выравнивания. Она определяет точку пересечения гиперповерхности регрессии с осьюy. Значенияb₁, b₂, …, b_mявляются оценками коэффициентов регрессии. Коэффициент регрессииb_kизмеряет усредненное частное влияние изменения переменнойx_k,k= 1, 2, …,m, в предположении, что остальные объясняющие переменные(x₁, x₂, …, x_k-1, x_k, x_k+1, …, x_m)остаются без изменения на постоянном уровне. Поэтому с точки зрения статистической методологии нет различия между множественной и частной регрессией. По этой причине в литературе параметрыb_k,k= 1, 2, …,mназываются как коэффициентами множественной, так и частной регрессии. Но заключение о том, что для определения коэффициентов регрессии достаточно определить несколько простых линейных регрессийyнаx_k,k= 1, 2, …,mявляется ошибочным. Для достоверных оценок нужны методы оценивания, учитывающие многосторонние связи совместно зависимых переменных. Наиболее часто используют двухшаговый метод наименьших квадратов, который является обобщением метода наименьших квадратов.

Рассмотрим сначала линейную множественную регрессию с двумя объясняющими переменными:

Метод наименьших квадратов приводит к условию:

, откуда

После дифференцирования S(b₀, b₁, b₂)по каждому из параметровb₀, b₁, b₂и приравнивания к нулю всех частных производных функцииS(b₀, b₁, b₂)по каждому из параметровb₀, b₁, b₂, получаем следующую систему нормальных уравнений:

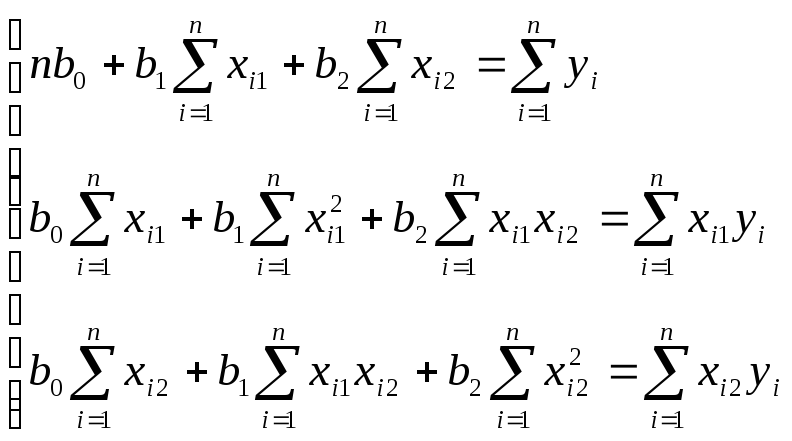
Решить полученную систему нормальных уравнений относительно неизвестных параметров можно по формулам Крамера.

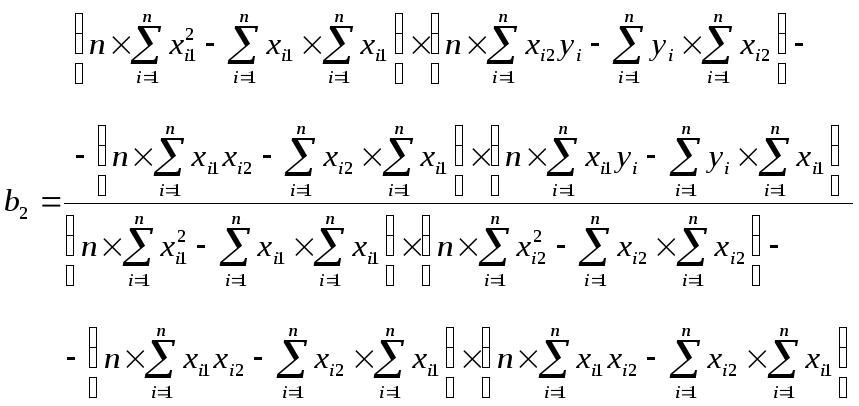
Коэффициенты множественной или частной регрессии можно представить через дисперсии и ковариации:

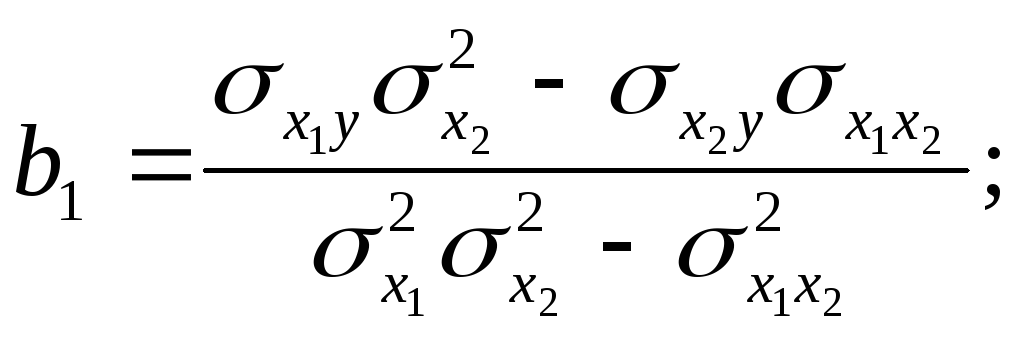
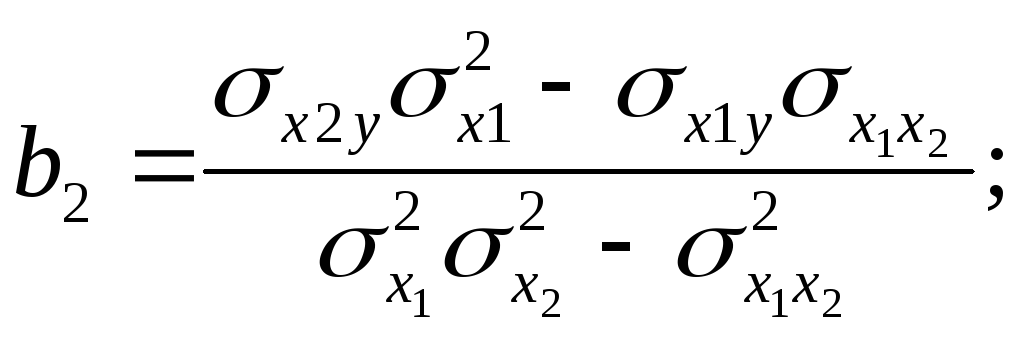
где

Пример

Построим линейную множественную регрессию общей суммы налогов и платежей на общую сумму поступлений по налогу на добавленную стоимость и налогу на прибыль (доход).

Время наблюдения	y(общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб.	x1(общая сумма поступлений в консолидированный бюджет РФ по налогу на прибыль), млрд. руб.	x2(общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб.
январь	38,9	5,6	13,4
февраль	45,3	6,7	15,4
март	61,1	13,1	16,7
I квартал	145,3	25,3	45,5
апрель	70,4	16,9	16,2
май	63,8	18,4	13
июнь	67,7	19,1	15
II квартал	201,9	54,4	44,2
I полугодие	347,2	79,8	89,7
июль	70,6	16,1	20,8
август	78,9	23,3	16,4
сентябрь	73,2	19,2	17,4
III квартал	222,7	58,6	54,6
9 месяцев	569,9	138,3	144,3
октябрь	78,1	16,1	23,6
ноябрь	103	31,8	23,9
декабрь	133,4	35,4	34,4
IV квартал	314,5	83,3	81,9
II полугодие	537,2	141,9	136,5
январь-декабрь	884,4	221,6	226,1

Σy	Σx1	Σx2	Σx1y	Σx2y	Σx1^2	Σx2^2	Σx1x2
884,4	221,6	226,1	18614,15	18154,57	4931,19	4667,94	4605,29

Полученные значения b₁ и b₂подставим в уравнение

и выразим b₀.

Для описания линейной множественной регрессии с количеством объясняющих переменных больше двух будем использовать матричное исчисление. Пусть

, или

Введем фиктивную переменную x₀полагаяx_i0= 1,i=1, 2, …,n.

Положим

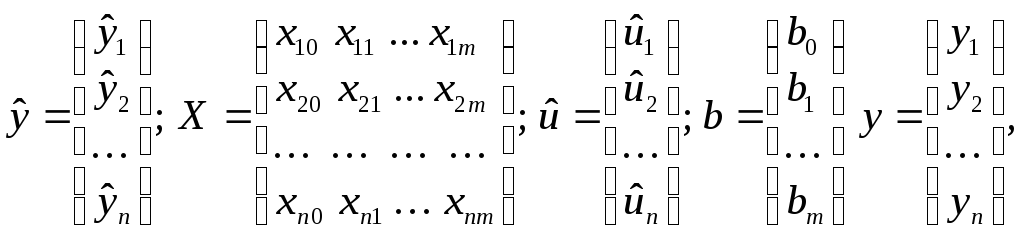
где x_ij– переменная для обозначения переменнойx_jпри наблюденииi,j= 1, 2, …,m;i= 1, 2, …,n.

Тогда уравнение регрессии запишется следующим образом:

Применяя метод наименьших квадратов, получим:

,

где А^t- матрица, транспонированная кА. Подставляя вместоŷв последнюю формулуXb, получаем

Дифференцируя последнее выражение по bи приравнивая его к нулю, получаем:

Нормальное уравнение имеет следующий вид:

Если матрица X^tX обратима, то