113

Высшая математика (краткий курс лекций)

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

§1. Понятие множества. Некоторые сведения о математической логике.

§2. Числовые множества. Множество действительных чисел.

§3. Числовые промежутки.

§4. Модуль действительного числа.

ГЛАВА 2. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

§1. Понятие функции и способы ее задания.

§2. Основные характеристики функций.

§3. Элементарные функции.

§4. Приложение функций в экономике.

ГЛАВА 3. ПРЕДЕЛЫ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ

§1. Числовая последовательность и ее предел.

Понятие предела является фундаментальным в математическом анализе. Начальные сведения о пределах встречаются еще в школьном курсе. Например, в алгебре с понятием предела связан вопрос о сумме членов бесконечной убывающей прогрессии, в геометрии – вопрос о вычислении длины окружности, площадей плоских фигур и поверхностей, объемов тел вращения.

В курсе математического анализа с помощью предела вводятся понятия производной, определенного интеграла.

Ознакомимся с понятием числовой последовательности и ее предела.

Определение.Если каждому натуральному числуnпоставлено в соответствие числох_n, то говорят, что заданапоследовательность

x_1, х₂, …, х_n = {x_n} (1.1)

Общий элемент последовательности является функцией отn.

x_n = f(n)

Таким образом, последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Примеры.

1⁰) {x_n} = {3n} или {x_n} = 3; 6; 9; 12; …

2⁰) {x_n} = {} или {x_n} = 1;;;; …

3⁰) {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

4⁰) {x_n} = {sinpn/2} или {x_n} = 1; 0; -1; 0; …

5⁰) {x_n} = {6} или {x_n} = 6; 6; 6; 6; …

Для последовательностей можно определить следующие операции:

1. Умножение последовательности на число m:m{x_n} = {mx_n}, т.е.mx₁,mx₂, …

2. Сложение (вычитание) последовательностей: {x_n}±{y_n} = {x_n±y_n}.

3. Произведение последовательностей: {x_n}×{y_n} = {x_n×y_n}.

4. Частное последовательностей: 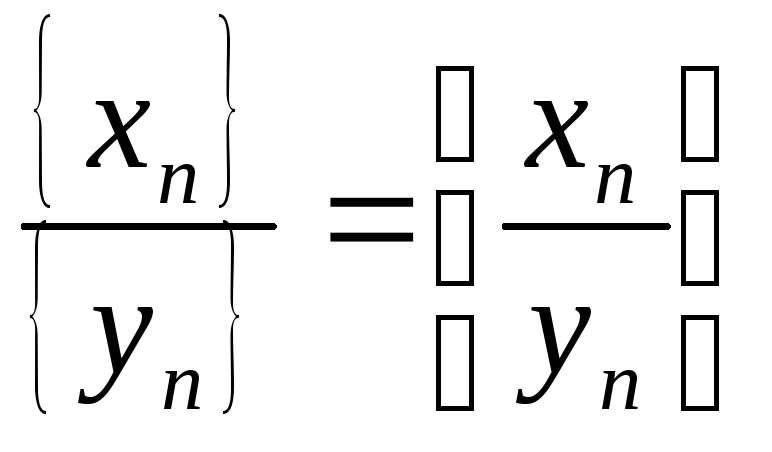при{y_n} ¹ 0.

Замечание.Если переменнаяx_n принимает значенияx_1, х₂, …, х_n,…, то говорят, что эта переменная «пробегает» числовую последовательность{x_n}. Такую переменную называют «упорядоченной». Часто упорядоченную переменную отождествляют с числовой последовательностью, которую она «пробегает» и обозначаютx_n. Переменнаяx_n не является непрерывной, она –дискретная.

Заметим, что n(номер) можно увеличивать неограниченно, пишутn→∞и последовательность (1.1) являетсябесконечнойчисловой последовательностью.

Вернемся к рассмотренному примеру 1⁰): {x_n} = {3n} или {x_n} = 3; 6; 9; 12; … На данном примере можно заметить, что приn→∞переменная величинаx_nтоже неограниченно возрастает. Такие величины называют бесконечно большими.

Определение.Переменная величинаx_nназывается бесконечно большой, если для любого (сколь угодно большого) М>0 можно найти такой номерn=N,начиная с которого все последующие значения переменной будут удовлетворять неравенству:

|x_n| ³M

Рассматривая пример 2⁰), можно заметить, что величинаx_n=→ 0 приn → ∞. Такие величины называютсябесконечно малыми.

Рассмотрим еще один пример: {x_n} = {} или {x_n} = 0;;;…

По мере возрастания номера nчлены числовой последовательности приближаются к числу 1. Говорят, что 1 – предел этой числовой последовательности. Точно так же в примере 2⁰) 0 – предел этой последовательности. Кратко это записывается так .

Определение. Окрестностью точкианазывается любой интервал (α, β), содержащий точкуа. В частности, симметричный интервал (а - ε;а+ ε), где ε > 0, называется ε-окрестностью точкиа.

Замечание.х (а - ε;а+ ε)

В общем случае, если последовательность {x_n}имеет своим пределом числоа, то это записывают так .

Геометрически это означает, что начиная с некоторого номера n=N,N+1,N+2, …все члены последовательности попадают в ε-окрестность точкиа. (ε – достаточно малое положительное число) или

Последовательности 3⁰),4⁰) не имеют предела (расходятся). Последовательность, которая имеет предел – сходится.

Определение.Числоаназываетсяпределомпоследовательности {x_n}, если для любого положительногоe>0 существует такой номерN, что для всехn>Nвыполняется условие:

Это записывается:

В этом случае говорят, что последовательность {x_n} сходитсяка приn®¥.

Свойство:Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример.Доказать, что предел последовательностиlim .

Пусть при n>Nверно , т.е.. Это верно при, таким образом, если заNвзять целую часть от, то утверждение, приведенное выше, выполняется.

Пример.Показать, что приn®¥последовательность 3, имеет пределом число 2.

Итого: {x_n}= 2 + 1/n; 1/n=x_n– 2

Очевидно, что существует такое число n, что, т.е.lim {x_n}= 2.

Теорема.Последовательность не может иметь более одного предела.

Доказательство.Предположим, что последовательность {x_n}имеет два пределаa иb, не равные друг другу, т.еx_n ® a; x_n ® b; a ¹ b.

Тогда по определению существует такое число e>0, что

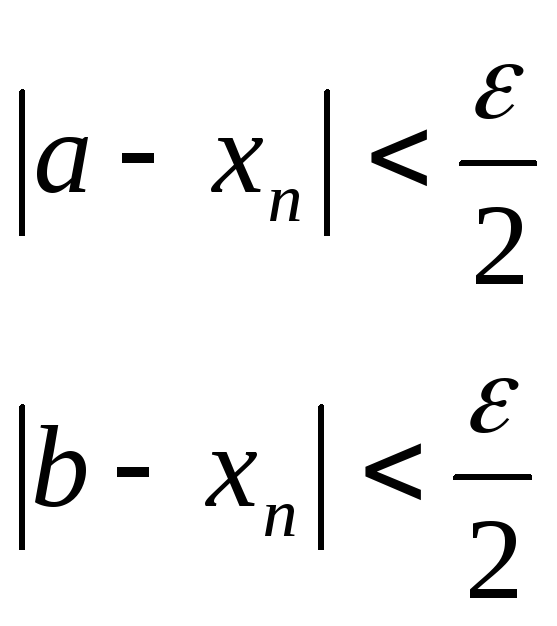
Запишем выражение:

А т.к. e-любое число, то, т.е.a=b. Теорема доказана.

Замечание.Говорят, чтонепрерывнаяпеременнаях→а, если эту переменную можно представить как бесконечное число числовых последовательностей, каждая из которых имеет пределом числоа.

Переменная хстремится каслева (справа), если все члены последовательностей, имеющих пределом числоа,

х→а-0

х→а+0

Переменная х→ +∞, если для любого сколь угодно большого М>0 найдетсях, начиная с которого все следующие значенияхбудут больше М :х> М их→ -∞, если для любого сколь угодно большого М>0 найдетсях, начиная с которого все следующие значенияхбудут меньше - М :х<- М. В этих случаях переменнаяхназывается бесконечно большой.