8. Теорема Барроу. Производная определенного интеграла по переменному верхнему пределу равна подинтегральной функции в точке, равной верхнему пределу, т.Е.

Доказательство.

По формуле Ньютона-Лейбница имеем Следовательно:

Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подинтегральной функции. Действительно, если обозначить , то(x) = f(x), то очевидна справедливость формулы , которая выражаетсвязь между определенным и неопределенным интегралами.

§5. Вычисление определённого интеграла.

5.1. Формула Ньютона – Лейбница.

.

Например,

5.2. Интегрирование подстановкой. Замена переменной.

Теорема.Если:

1) и её первообразнаянепрерывны на отрезке.

2)множество значений функции приявляется множество, заполняющее отрезок от [а;в].

3) и при этом,

то (*)- формула замены переменной.

Доказательство: Пусть F(x)– первообразная для функцииf(x) на отрезке [а;в].

Тога по формуле Ньютона- Лейбница (1).

Покажем, что (1) равна (*).

Тогдаявляется первообразной для функции (1) на отрезке.

Тогда по формуле Ньютона – Лейбница

Отметим некоторые особенности этой формулы:

1) при вычислении определённого интеграла по формуле (1) возвращаться к старой переменной не надо.

2) часто вместо подстановки применяют подстановку.

3) обязательно надо менять пределы интегрирования при замене переменной.

Примеры:

1)

5.3. Интегрирование по частям в определённом интеграле.

Теорема:Если функцииu=u(x)иv=v(x)имеют непрерывные производные на [а;в], то имеет место

(2).

Доказательство: для всех: любые (uv)’=u’v+uv’=>uvявляются первообразной дляu’v+uv’;тогда при любыхсправедливо равенство:

Примеры:

§6. Геометрическое применение определённого интеграла.

6.1. Вычисление площадей плоских фигур.

Из геометрического смысла интеграла следует, что площадь криволинейной трапеции, расположенной выше оси абсцисс (f(x)≥0), равна определенному интегралу:

(1)

S-?: y=; y=0; x=0;x=1.

Если криволинейная трапеция расположена ниже оси Ох (f(x)<0) ,то площадь криволинейной трапеции равна определенному интегралу, взятому с противоположным знаком («-»).

(2)

Пример: у=; у=0; х=-1; х=-2.

х=-2 х=-1 у

S=

х

Формулы 1 и 2 можно объединить: S=(3)

Площадь фигуры ограниченной кривыми и, прямымих=а и х=впри условии, чтодля всех, находятся по формуле(4)

у

а в х

Пример: Найти Sтрапеции, ограниченной;.

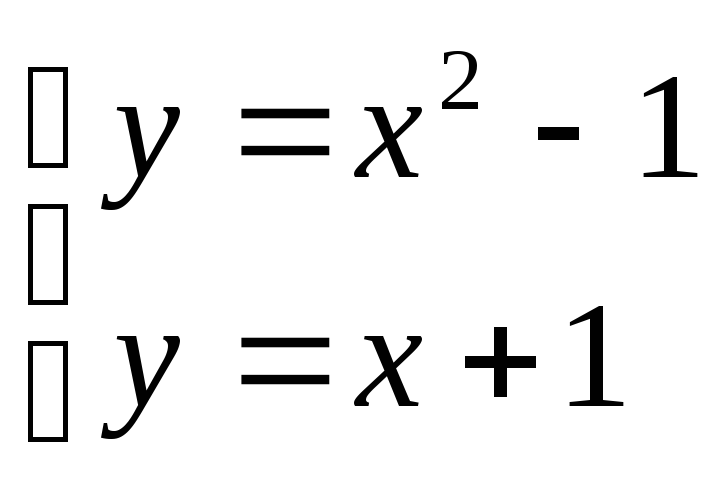
Если плоская фигура имеет «сложную» форму, то прямыми, параллельными оси Оуеё можно разбить на части, так, чтобы можно было применить уже известные формулы.

;

Пример: ВычислитьSфигуры, ограниченной осьюОх, и у=sin x; y=cos x.

sin x=cos x*cos x

tg x=1

x=; n

Аналогично если криволинейная трапеция ограничена прямыми у=с и у=d,осью Оу и непрерывной кривой х=φ(у)0

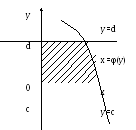
Пример: Найти Sфигуры, ограниченной кривой; у=8 и осью Оу.

6.2. Вычисление объёма тела вращения.

1)Пусть криволинейная трапеция аАВв, ограниченная графиком неопределённой функцииy=f(x)0, прямымих=а; х=в и отрезком оси абсцисс, вращающейся вокруг осиОх.

Эта трапеция опишет тело, которое называется телом вращения. Найдем его объём(V).

Разделим отрезокна части точками. Через точки деления проведём плоскости, перпендикулярные оси Ох, в результате получаются поперечные сечения, которые представляют собой окружности радиуса. В результате такого деления всё тело разделяется на

i-го тела с высотой

Тогда, объём всего тела.

2) Внутри каждого частичного отрезка возьмём точкуи проведём через неё поперечное сечение. Заменим каждыйi-тый слой с объёмомс высотойи основанием, полученным в результате сечения через точку().

3) Составим сумму объёмов элементарных цилиндров (1)

Сумма (1) есть интегральная сумма на отрезке. Эта сумма ≈ объёму телаV.

4) Выберем шаг деления - наибольшее изd, при.

5) За объём тела вращения примем limинтегральной суммы (1) при, т.е.(2)=

Если предел (2) существует и конечен, а f(x)- непрерывная функция, то предел (2) существует и равен определённому интегралу функциина.

=

(3)

Замечание: Если криволинейная трапеция cCDdограничена графиком напрерывной функции; прямыми у=с, у=dи отрезком оси ординат, вращающимся вокруг оси Оу, этот объём тела вращения равен(4)

Примеры:

1)Вычислить объём тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями ; у=0, х=2

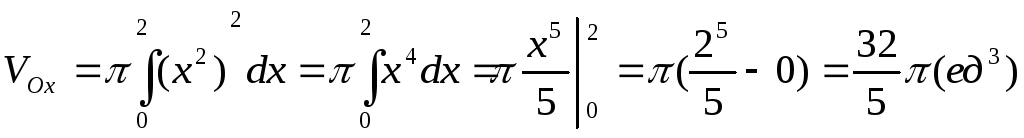
у

2) Найти объём тело, полученного вращением вокруг оси Оу фигуры, ограниченной ; х=0; у=4.

.