§7. Несобственные интегралы с бесконечными пределами (несобственные интегралы первого рода).

существует, если выполняется условие:

1. промежуток интегрирования - конечный.

2. Подъинтегральная функция f(x) непрерывна на.

Такие интегралы называют собственными.

Если хотя бы одно из этих условий нарушается, то такой интеграл называют несобственным.

когда нарушается первое условие, т.е. промежуток интегрирования бесконечен либо на верхнем, либо на нижнем, либо на обоих.

Пусть функция f(x) непрерывна на. Если существует конечный пределlim f(x)dx, т.е. его называют несобственным интегралом первого рода и обозначают:

(1)

Если lim(1)=∞ или не существует, то говорят, что данный интеграл расходится.

Аналогично определяется несобственный интеграл на (2).

Несобственный интеграл с двумя бесконечными пределами определяется формулой: (если f(x) непрерывна для всех)

Геометрический смысл:

Если функция ; то промежуток (а;+∞).

Примеры: вычислить несобственные интегралы и установить их расходимость.

1) - расходится.

2)- сходится.

3) - сходится.

Интеграл Пуассона.

Несобственный интеграл -интеграл Пуассона. Это равенство доказано.

§8. Кратные интегралы.

8.1.Двойные интегралы.

Пусть область Д– некоторая замкнутая и ограниченная область на плоскости ХОУ.

Ив этой области определена некоторая непрерывная функцияz=f(x;y).

Разобьём область Днаn- произвольных частей. Площади каждой части обозначимВ каждой из частичных областей возьмём произвольную точку:.

(1)- интегральная сумма для функцииz=f(x;y)на областиД.

Назовём диаметром области d– наибольшее расстояние между граничными точками этой области.

Пусть - шаг разбиения.

Определение.Если интегральная сумма (1) имеет предел при, то этот предел называется двойным интегралом от функцииz=f(x;y)по областиДи обозначается:

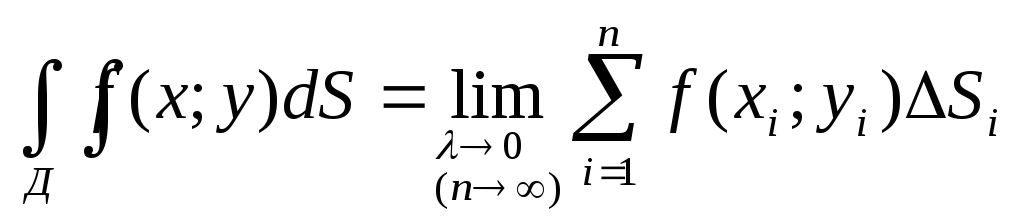(2)

dS=dxdy

При вычислении двойного интеграла используется теорема о сведении двойного интеграла к повторному, т.е. т.о. возможности дважды применить процесс обычного интегрирования.

Теорема.Пусть функцияz=f(x;y)ограничена и интегрируема в области Д. Область Дограничена сверху и снизу двумя непрерывными кривыми.

Пусть для каждогохиз отрезкасуществует определенный интеграл.

- (внутренний интеграл.)

Тогда существует повторный интеграл: и двойной интеграл функцииf(x;y)по областиД:(3)

В формуле (3) при вычислении внутреннего интеграла переменную х считают Const.

Пример: Найти двойной интеграл: , если областьДограниченау=х, у=2х, х=0,х=ln2.

(*)

(смотреть*)

8.2. Тройные интегралы.

Пусть область V– некоторая замкнутая и ограниченная область в пространствеxOyz.

В этой области определена произвольная ограниченная функция u=f(x;y;z). Разобьём областьVнаn-произвольных частей.- объём этих частей.

В каждой из частей возьмём точку и составим произведение:

(4)- интегральная сумма для функции

u=f(x;y;z)в областиV.

- шаг разбиения – наибольшее из всех диаметров частичных объёмов.

Если существует предел интегрирования суммы (4) при и он равен конечному числу, то он называется тройным интегралом от функцииu=f(x;y;z)по областиV:

(5)

(dV=dxdydz)

Теорема. (смотреть график выше) Если область Vпредставляет из себя следующее:

ограничена поверхностями:

- проекции этих поверхностей на плоскости хОу.

х=а

х=в

И тогда формула для вычисления тройного интеграла: