Безруков А.В. ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

z 0 ,

пути. Это приводит к утверждению, известному под названием теоремы Коши: интеграл. взятый по замкнутому контору от функции, аналитической всюду внутри этого контура и на нем, равен нулю.

П.2.2. Вычеты

Выше говорилось, что интеграл не зависит от пути, если подынтегральная функция не обращается в бесконечность. Рассмотрим пример, в котором подынтегральная функция обращается в бесконечность.

			z			z
Пусть	I		dz	. Здесь	f z	1	обращается в бесконечность при z 0 .

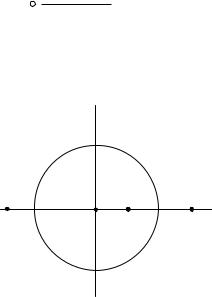
Вычислим интеграл по замкнутому пути, обходящему в положительном

направлении (т.е. против хода часовой стрелки) точку										z 0 ,	например по
окружности с радиуса		r		с		центром в				начале	координат
(рис. П.2.2).
	y			На		такой		окружности z re j . где r -
	Z			радиус окружности, а переменная
				изменяется от 0 до 2 .
	r			Тогда dz re j jd и
0		x			dz	2 re j d
									2 j .
					z		re j
				C		0

Интеграл по замкнутому кругу оказался не равным нулю.

Рисунок П.2.2

Рассмотрим еще один пример. Пусть надо вычислить интеграл

cosz3 zdz

по замкнутому контуру, обходящему в положительном направлении начало координат которое является особой точкой для подынтегральной функции.

Вспомнив разложение функции cos z				вокруг точки z 0 в степени ряд
Тейлора.
cos z 1	z 2		z 4		z6	...
2!		4!		6!

можем написать

131

cos z		1		1		z			z 2	...
z3		z3
				2!z		4!		6!

В этом примере при		z 0 подынтегральная функция стремится к
бесконечности со скоростью		1			; такая особая точка называется полюсом
		z		3
третьего порядка.

Рассмотрим теперь полюс общего вида. Если (однозначная!) функция f (x) имеет в некоторой точке полюс порядка n , то вокруг этой точки он разлагается в так называемый ряд Лорана.

f (x) C

n

(z a) n C

n 1

(z a) n 1

... C

1

(z a) 1

C

0

C (z a) C

2

(z a)2

...

1

...

C n

C n 1

...

C 1

C0

C1 (z a) C2 (z a)

2

...

(z a)n

(z a) n 1

(z a)

по целым положительным и отрицательным степеням (z a) , начиная с n-й степени. Пусть требуется вычислить интеграл

f (z)dz

по контуру, обходящему точку z a в положительном направлении и не содержащему внутри себя других особых точек. Как было показано, от заданного интеграла можно перейти к интегралу по маленькой окружности с центром в точке a , а вблизи этой точки воспользоваться разложением в ряд Лорана. Можно показать, что после интегрирования по замкнутому контуру интеграл от всех членов окажутся равными нулю, за исключением (см. н/о).

c1

z adz 2jc 1

Этому значению окажется равным и весь интеграл. Коэффициент c 1 при (-1) и степени (z a) ряда Лорана имеет специальное название: вычет функции f (z) в точке a , таким образом, интеграл равен

2j Вычz a f (z)

В случае, если внутри замкнутого контура находятся несколько особых точек, интеграл по этому контуру будет равен произведению 2j на сумму вычетов подынтегральной функции во всех особых точек, расположенных внутри контура интегрирования

f (z)dz 2j[Вычz a1 f (z) Вычz a2 ... Вычz an f (z)]

( L)

Покажем, как вычисляется вычет для наиболее важного случая полюса первого порядка. Такой полюс обычно получается, если подынтегральная

132

z k

функция f (z) представляет собой отношение двух конечных функций:

f (z) g(z) / h(z) , причем в некоторой точке z a числитель отличен от нуля, а знаменатель имеет нуль первого порядка, т.е. разложение знаменателя по

степеням (z a) начинается

с члена первой степени. Записав разложение

числителя и знаменателя в ряд Тейлора вокруг точки z a , получим

g(a) g'(a)(z a)

g''(a)

(z a)2 ...

f (z)

2

h'(a)(z a)

h''(a)

(z a)2 ...

2

Вблизи точки z a правую часть может заменить на

g(a)

h'(a)( z a)

Поэтому вычет, т.е. коэффициент при (z a) 1

в данном случае равен

Вычz a

f (z)

g(a)

(П.2.3)

h'(a)

Рассмотрим пример. Пусть требуется вычислить интеграл

z 1

I ( L) (z 1)sin z dz

где (L) – окружность радиуса r с центром в начале координат (рис.

П.2.3).

Z

	1

Рисунок П.2.3

В этом примере неопределенный интеграл не выражается через элементарные функции; однако интеграл по замкнутому контуру мы найдем без труда! Для этого заметим, что подынтегральная функция имеет полюсы в точках z 0 z 1 и ( k - целое число).

Из этих точек, изображенных на рисунке П.2.3, внутрь попадают только две: z 0 и z 1. Поэтому можем записать (в силу вышеизложенному)

I 2 i[Вычz 0 f (z) Вычz 1 f (z)]

133

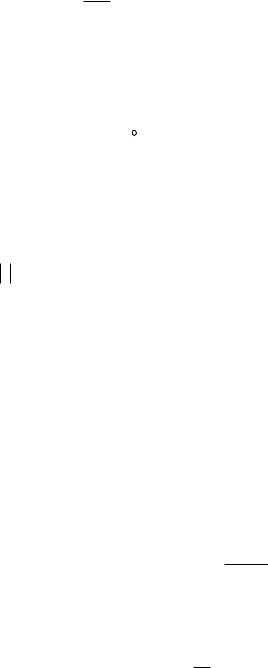
Так как в каждой из этих точек знаменатель имеет нуль первого порядка, а числитель отличен от нуля, то мы имеем два полюса первого порядка и вычеты в них можно подсчитать по формуле П.2.3.

В данном примере

g(z) z 1,

h(z) (z 1)sin z,

h'(z) sin z (z 1)cosz,

откуда Вычz 0

f (x)

g(0)

1

1,

Вычz 1 f (z)

g(1)

2

,

h'(0)

1

h'(1)

sin1

откуда I 2 i( 1 sin2 1) 8,65i

Действительно, числа, стоящие в ряду правее не имеют особых точек. Покажем, что и интегралы от левых членов ряда также равны нулю.

У интеграла
	1	dz	(m=2,3,4)
	z m
подынтегральная функция имеет особенность (обращаю в
бесконечность при z 0 ). Однако			этот интеграл равен нулю по любому

замкнутому контуру как не охватывающему эту точку, так и охватывающему ее (но не проходящему через нее). Покажем это. Возьмем интеграл по окружности z r . Положим z re j , тогда после простых преобразований интеграл примет вид

2

ir1 m ei(1 m) d

0

Непосредственное вычисление показывает, что он равен нулю при любом целом m 1.

(Вообще-то, интеграл по замкнутому контуру, охватывающему особые точки не равен нулю, если неопределенный интеграл представляет собой неоднозначную функцию).

В нашем случае при m 1 он равен

z m 1

z m dz m 1 C

т.е. представляет собой однозначную функцию, в отличии от случая m 1, когда

dzz ln z C

Вто же время Lnz – неоднозначная функция, поскольку

ln x ln x ln1 ln x 2 in

134

т.к.

e2 ni cos(2 ni) j sin(2 ni) 1

П р и л о ж е н и е 3

П.3. Представление частотной характеристики фильтра с помощью нуль – полюсных диаграмм

Нуль полюсной диаграммой цифрового фильтра называется график, на котором нули и полюсы передаточной функции фильтра изображаются в z- плоскости относительно окружности единичного радиуса.

Для оценки ЛЧХ цифрового фильтра с помощью нулю – полюсной диаграммы преобразуем вначале общее выражение передаточной функции (5.6), используя следующее положение: "каждый многочлен f (x) степени N относительно X может быть единственным способом представлен в виде произведения постоянной величины и линейных множителей вида (x xk ) "

N

f (x) p0 (x xk )

(П.3.1)

k 1

где p0 - постоянная величина;

xk - корни многочлена

f (x) , в том числе которых комплексные корни

могут быть только в виде сопряженных пар.

Первый шаг преобразования ПФ (5.6) состоит в изменении знака

показателей переменной z:

M

b

b z

1

b z

2

... b

z

M

z M bM k z k

H (z)

M

k 0

0

1

2

(П.3.2)

1 a z 1

a

z 2 ... a

z L

L

z

L

k

1

2

L

aL k z

k 0

Используя равенство (П.3.1), представим выражение (П.3.2) в

следующем виде:

M

(z z0k )

H (z) a

z L M

k 1

,

(П.3.3)

0

L

(z znk )

k 1

где z0k - M-нулей;

znk - L-полюсов функции H (z)

При определении АЧХ цифрового фильтра считают, что на его входе действует незатухающая синусоида

z Aexp( j )	(П.3.4)
	135

где A – 1-амплитуда;

ˆ
T - нормированная круговая частота
Подставляя последнее выражение в (П.2.3) получим комплексный
коэффициент передачи
	M
	ˆ	]
H ( j ) p0 exp( j )	[exp( j ) z0k			(П.3.5)
	L	,
ˆ	k 1
	ˆ	]
	[exp( j ) znk

k 1

где ˆ (L M ) . Учитывая, что exp( j ) 1, определим АЧХ цифрового фильтра как модуль H( j ˆ) :

		M
				ˆ	]
				[exp( j ) z0k
H ( j ) p0		L				(П.3.6)
ˆ		k 1
				ˆ	]
				[exp( j ) z0k

k1

Вкаждом сомножителе числителя (П.2.6) составляющие exp( j ˆ ) и z0k могут быть представлены в z-плоскости векторами. тогда векторные разности

Nk exp( j ˆ ) z0k Nk exp( jk 0)

также представляют собой вектора длиной N k , как это показано на рисунке П.1.1 а) для случая двух комплексно – сопряженных нулей.

	N1
		z01
	ˆ	P2	P1
	exp( j )
		zn2
	ˆ	P3
-1	1		zn1
	N2	zn3

а)	z02	б)

Рисунок П.3.1 Нуль – полюсные диаграммы цифровых фильтров:

а) для случая нулей; б) для случая полюсов.

136

Таким образом, числитель выражения (П.2.6) может быть представлен следующим образом:

M		M				M
[exp( j ) zok ]			Nk			Nk	(П.3.7)
	ˆ
k 1		k 1				k 1

Аналогично запись получается и для знаменателя:

L		L				L
[exp( j ) znk ]			Pk			Pk ,	(П.3.8)
	ˆ
k 1		k 1				k 1
где N k и Pk	- длины векторов k-х разностей векторов числителя и

знаменателя ПФ.

В соответствии с формулами (П2.7) (П.2.8) выражение (П.2.6) для АЧХ можно переписать в виде

	L
H ( ) p0	Nk	(П.3.9)
	L
ˆ	k 1

Pk

k 1

Описанный способ определения АЧХ удобен тем, что для ее оценки достаточно располагать записью ПФ.

Сразу же отметим, что нули и полюсы, расположенные в начале координат (z=0), удалены от любой точки на окружности единичного радиуса на одинаковое расстояние r=1. Следовательно, такие нули и полюсы не влияют на форму АЧХ.

Чем ближе нуль расположен к окружности единичного радиуса, тем меньше коэффициент передачи цифрового фильтра не соответствующей частоте. Если ряд нулей расположен непосредственно на оси единичного радиуса, то на частотах, соответствующих листу расположения нулей, коэффициент передачи цифрового фильтра равен нулю. *(п/о)

В качестве первого примера рассчитаем АЧХ низкочастотного цифрового фильтра первого порядка. Передаточная функция фильтра описывается выражением

H (z)	b	(П.3.10)
	1 az 1

и имеет один полюс zn a . В соответствии с выражением (П.2.9) АЧХ рассматриваемого фильтра с точностью до постоянного множителя находится по следующей формулу.

ˆ	1	(П.3.11)
H ( ) b p
		137

Для определения расстояния Р (рис. П.3.2) используем известную формулу из курса геометрии, которая связывает длину стороны С с длинами сторон треугольника А и В и косинусом угла ˆ между ними.

*) связь АЧХ с расположением полюсов и нулей можно продемонстрировать с помощью рисунка (П.3.2)

2 1

-1 х

х 1

Рисунок П.3.2 Связь АЧХ с расположением нулей и полюсов:

а) нуль – полюсная диаграмма; б) АЧХ. 1	2
		2
а)		б)

C 2 A2 B2 2A Bcos ˆ

Согласно этой формуле и рисунку П.2.3

exp( j ˆ )

ˆ Р

-1

0 Zn=b

1

138

Рисунок П.3.3 К расчету АЧХ цифрового фильтра

P	exp( j ˆ )	2 z 2	2z	n	exp( j ˆ )	cos( ˆ )	1 a2 2a cos ˆ
		n

Подставив последнее соотношение в формулу (П.2.11), получим следующее выражение для АЧХ

H ( ˆ )				b
			a 2	2a cos ˆ
1

Вход АЧХ такой цифровой RC-цепи (и ее аналогового прототипа показан на рис. П.2.4).

H ( ˆ )

		H 2 ( ˆ )
	2	3	H ( ˆ )	ˆ
			4

Рисунок П.2.4. Вид АЧХ цифровой RC-цепи и его аналогового прототипа.

Несколько усложним постановку задачи и рассмотри цифровой фильтр 2-го порядка с комплексно сопряженными нулями и полюсами (рис. П.2.5).

Imz

ˆ

P

N

ˆ ˆ 0

0

Rez

Рисунок П.3.5

139

Для упрощения расчета АЧХ рассматриваемого фильтра учтем ряд обстоятельств. Во-первых, заметное различие в расстояниях Р(до полюса) и N(до нуля) имеет место только в небольшой области частот вблизи значенияˆ 0 (см. рис. П.3.5). В удаленных от частоты ˆ 0 областях расстояние P и N практически одинаковы, следовательно, коэффициент передачи цифрового фильтра, равны отношению P/N, в этих областях к единице и практически не меняется. Таким образом, при расчете АЧХ достаточно учитывать только

расстояния до нуля и полюса, расположенные в области вблизи 0 . При
			ˆ
изменении текущей частоты вектор exp( j )		отклоняется от в этой области на
угол 0	(см. рис.П.3.5). Во-вторых,	так как резкое изменение АЧХ
ˆ ˆ	ˆ	0
происходит в небольшом интервале частот			, то соответствующая
		ˆ ˆ	ˆ

этому интервалу дуга окружности единичного радиуса может бать аппроксимирована прямой. Длина дуги равна R , где R=1 – радиус единичной окружности. Учитывая перечисленные обстоятельства, расчет АЧХ будем проводить с использованием геометрических построений, проведенных на рис. П.3.6.

R
ˆ
Р	x=R-Rn
х	y=R-R0
N

Рисунок П.2.6. К расчету селективного фильтра

В соответствии с выражением (П.2.9) и рисунком (П.2.6)

2

Ni

ˆ

) ,

(П.2.12)

H ( ) (

P

i 1

i

где

Ni

, (П.3.13)

( R)

2

(R R0i )

2

( )

2

(1 R0i

/ R)

2

( )

2

(1 r0i )

2

ˆ

ˆ

ˆ

Pi

( R)

2

(r R*i )

2

( )

2

(1 Rni

/ R)

2

( )

2

(1 rni )

2

ˆ

ˆ

где

T 2 f / f Д , R0 и Rn – расстояние от центра окружности до

ˆ

нуля и полюса соответственно, r0

и rn –

их значения, нормированные к

радиусу окружности.

140