Безруков А.В. ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

Размерность

ДПФ

N2 ДПФ2

N4 ДПФ 4

2i 1ДПФ N

2i 1

4ДПФ N

4

2ДПФ N

2

Начальные

условия

Длина последовательности

Этап

i

ν

1

ДПФ

ДПФ

ДПФ4

ДПФ4

ν-1

2

4

4

ДПФ N

ДПФ N

ДПФ N

ДПФ N

ν-i

i

2i 1

2i 1

2i 1

2i 1

ДПФ N

ДПФ N

ДПФ

N

2

ν-1

4

4

4

ДПФN

ДПФ N

ДПФ N

1

ν

2

4

2

Две

N

2 – точечных последовательностей

2

N

N

N

x(0), x(1),...,x

1

x

, x

1 ,...,x N

1

4

2

2

Рисунок 8.7

последовательности, при этом разность перед вычислением ДПФ умножается на комплексные экспоненты exp(-j2πm/N). Каждое из двух используемых здесь ДПФ размерность N/2.

Повторяя аналогичные рассуждения и математические преобразования для последующих этапов, получим общую формулу расчѐта ДПФ для произвольного i-го этапа.

	i 1		i		(k)
X	2m (k)	X m
	i 1				i	(k)
X	2m 1(k) X m
i , 1,...1,;
m 0,1,...,M 1;
	0,1,...,	L		1;
k
		2

X mi (k L2 );

X i (k L ) W k ;

m 2 L

(8.45)

81

где i-номер этапа, m-номер ДПФ, k-номер отсчѐта ДПФ, M 2 1 - количество ДПФ, L 2i - размерность ДПФ.

Поскольку комплексный экспоненциальный множитель в данном алгоритме применяются к результату вычисления двух величин, «бабочек» БПФ с прореживанием по частоте имеет несколько иную структуру (рис. 8.8)

X mi (k)

X mi (k L2 )

X 2i m1(k)

WLk

X i 1 (k)

2m 1

WLk

X mi (k) X mi (k L2 )

X mi (k ) X mi (k L ) WLk2

1

Рисунок 8.8 Направленный граф и структура «бабочек» БПФ с прореживанием по частоте

Она получается путѐм замены входа и выхода, а также обращения стрелки направленного графа «бабочки» алгоритма БПФ с прореживанием по времени, т.е. алгоритмы являются ДУАЛЬНЫМИ. Согласно принципу дуальности номера этапов в (8.45) меняются по убыванию.

8.4.5 Пример вычисления 8-точечного ДПФ с помощью алгоритма БПФ с прореживанием по частоте

Для лучшего понимания алгоритма БПФ с прореживанием по частоте рассмотрим его на примере вычисления 8-точечного ДПФ.

Алгоритм БПФ представляет собой трѐхэтапную процедуры вычисления ДПФ по общей формуле (8.45) при i=3,2,1.

 Начальные условия задаются как:

X 3		(k) x(k)	(8.46)
	0
k 0,1,...,7

 Первый этап: i=ν=3. Определяются два 4-точечных ДПФ (8.45) при m=0 с учѐтом начальных условий (8.46):

X 2 (k) x(k) x(k 4);

0

X12 (k) x(k) x(k 4) W8k ;k 0,1,2,3.

Второй этап i=ν-1=2. Определяются четыре 2-точечных ДПФ (8.45)

при m=0,1;

82

X 1 (k) X 2 (k)

2m m

X 1 (k) X 2 (k)

2m 1 m

k 0,1.

X m2 (k 2);

X m2 (k 2) W4k ;

Третий этап i=ν-2=1. Определяется 8-точечных ДПФ (8.45) при m=0,1,2,3;

					X 0 (0) X 1 (0) X 1 (1);
						2m	m	m
							(0) X 1	(0) X 1	(1) W 0	;
					X 0
						2m 1	m	m	2
Значение	X 0	(0)	и	X 0	(0)	при m=0,1,2,3 и есть искомое 8-точечное
	2m			2m 1

ДПФ, отсчѐты которого следуют в бит-реверсивном порядке двоичных номеров;

X (0) X 0		(0);	X (2) X 0		(0);
	0			2
	X 0			X 0
X (4)		(0);	X (6)		(0);
	1			3
X (1) X 0		(0);	X (3) X 0		(0);
	4			6
	X 0 (0);			X 0	(0).
X (5)			X (7)
	5			7

Направленный граф алгоритма БПФ с прореживанием по частоте для 8- точечного ДПФ показан на рис. 8.9

X 03 (0) x(0)					X 02 (0)				X 01 (0)				W20		X (0) X	03 (0)
					X 02 (1)			W40	X 01 (1)						X (1) X 03 (1)
X 03 (1) x(1)
X 03 (2) x(2)				W80	X12 (2)				X11 (0)				W	0	X (2) X	03 (2)
														2
3		(3) x(3)		W 1		2	(3)	W 1	1		(1)					3	(3)
X 0				8	X1			4	X1						X (3) X 0
X 03		(4) x(4)		W 2		2	(0)		1		(0)				X (4) X	3
				8	X1				X 2				W20			0 (4)
								W 0
X 03 (5) x(5)					X	2	(1)		X	1		(1)			X (5) X 03 (5)
						1		4
										2
3				3
				W8		1				1							3
X 0 (6) x(6)					X		(2)		X			(0)			X (6) X			(6)
						1				3				0			0
													W2
						2		1
3								W4		1							3
		(7) x(7)			X1 (3)				X			(1)			X (7) X			(7)
X 0										3							0

Рисунок 8.9

83

log 2 N

8.4.6 Оценка выигрыша в количестве операций при вычислении ДПФ с помощью алгоритма БПФ с основанием 2.

Оценим выигрыш в количестве арифметических операций при вычислении N-точечного ДПФ с помощью рассмотренных алгоритмов БПФ с основанием 2. Любой из этих алгоритмов состоит из ν-этапов, где

log2 N .

Количество «бабочек» на любом i-м этапе алгоритма БПФ с прореживанием по времени и по частоте одинаково и, согласно (8.40), равно N/2. Для одной «бабочки» при фиксированных m и k требуются два сложения (для верхней и нижней формул) и одно умножение на поворачивающий множитель - всего три арифметические операции. Следовательно, для N/2 «бабочек» на каждом этапе необходимо 3N/2, а на всех ν-этапах - (3N/2)

арифметических операций с комплексными числами.

Порядок вычислительной сложности алгоритма БПФ оценивается как 0(N log 2 N ), в то время как при прямом вычислении ДПФ (8.20) он равен 0(N²). Наглядное представление о получаемом выигрыше в объеме вычислений в зависимости от длины N исходной последовательности можно получить из таблицы 8.2 (см. н/о).

8.4.7 Вычисление обратного ДПФ с помощью Алгоритма БПФ

Покажем возможность использования алгоритма БПФ для вычисления ОДПФ

		1	N 1
	X (n)		X (k)WN nk , n=0,1,…,N-1.
		N k 0

Выполним операцию комплексного сопряжения правой и левой частей равенства (символ *) и умножим обе части на N:

			N 1
		Nx* (n) X * (k)WNnk .
			k 0
Таблица 8.2
		Оценка вычислительной сложности			Оценка
	N	Прямое	Вычисление	с	выигрыша
		вычисление ДПФ	помощью	БПФ	N 2 /(N log 2 N )
		N 2	N log2 N
	8	64	24		2,7
	16	256	64		4,0
	32	1024	160		6,4
	64	4096	984		10,7
	128	16384	896		18,3
	256	65536	2048		32,0
			84

512	262144	4608	56,9
1024	1048576	10240	102,4
2048	4194304	22258	186,2

(продолжение)

Правая часть равенства представляет собой N-точечное ДПФ последовательности X * (k) , которое вычисляют с помощью одного из алгоритмов БПФ. После этого, вновь выполнив операцию комплексного сопряжения и разделив обе части равенства на N, получим искомую последовательность:

	1	N 1	*	nk
x(n)		X		(k)WN		, n=0,1,…,N-1.
	N k 0

Последовательность обработки для вычисления обратного БПФ изображена на рисунке 8.10

X real (m)				X real (n)
			: N
	Прямое
X imag (m)	БПФ			X imag	(n)
			: N
1		1

Рисунок 8.10

Второй метод вычисления обратного БПФ реализуется в соответствии со схемой, показанной на рисунке 8.11

X real (m)				: N	x
		Прямое
X imag	(m)	БПФ
				: N

Рисунок 8.11

В этой схеме нет необходимости возиться с сопряжѐнными последовательностями. Вместо этого мы просто меняем местами действительные и мнимые части последовательностей комплексных отсчѐтов. Чтобы понять, как работает эта схема, рассмотрим ещѐ раз выражение для обратного ДПФ, представив входную последовательность

85

X(m) в виде					действительной и мнимой части и помня, что
exp( j ) cos j sin запишем выражение обратного ДПФ
		1 N 1				2 j mn / N		1 N 1
x(n)			X (m)e						X real (m) jX image (m) cos(2 mn / N ) j sin(2 mn / N )
N m 0								N m 0
(8.47)
Перемножение комплексных членов (8.47) дает нам
		1 N 1
x(n)				X real (m) cos(2 mn / N ) Ximag (m) sin(2 mn / N )						(8.48)
		N m 0
j X real (m) sin(2 mn / N ) Ximag (m) cos(2 mn / N )

Формула (8.48) представляет общее выражение для обратного ДПФ и, как мы ниже покажем, реализуется схемой, представленной на рисунке 8.11. Поскольку X (m) X real (m) jX imag (m) , перестановка этих членов приводит

		X		(m) Xreal (m) jXimag (m)
Прямое ДПФ последовательности								(m) имеет вид x e j 2 nm / N
							X
					1 N 1
x(n)						Ximag (m) cos(2 mn / N ) X real			(m) sin(2 mn / N )	(8.49)
					N m 0
j X real (m) cos(2 mn / N ) Ximag (m) sin(2 mn / N )

Поменяв местами действительную и мнимую части результата этого ДПФ, мы получаем то, к чему стремились, а именно к соотношению (8.47).

9.ВВЕДЕНИЕ В ЦИФРОВЫЕ ФИЛЬТРЫ

9.1Основные определения и классификация цифровых фильтров

Под цифровыми фильтрами (ЦФ) в широком смысле понимают любую

цифровую	систему (цепь), которая	согласно заданному оператору
~	(рис.15.1) осуществляет преобразование действующей на еѐ
y(n) F x (n)
	~	полезного сигнала x(n) и помехи
входе аддитивной смеси X (n) x(n) (n)

(n)

~

x (n)

y(n)

Прямое

БПФ

~

F x (n)

Рисунок 9.1

Цифровой фильтр в узком смысле – это частотно избирательная цепь, которая обеспечивает селекцию цифровых сигналов по частоте, например: фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ), режекторные фильтры (РФ).

86

Цифровые фильтры делятся на два обширных класса: нерекурсивные (КИХ) и рекурсивные (БИХ). В свою очередь, в каждом из этих классов выделяют линейные и нелинейные. Оператор линейного фильтра отвечает свойству линейности:

~	~	~	~
F a1x1	(n) a2 x2	(n) a1F x1	(n) a2 F x2 (n)
Формой представления линейного оператора F, в частности, является
разностное уравнение.
Будем полагать также,			что изучаемые фильтры физически невозможны,

т.е. выполняется условие причинности: при нулевых начальных условиях реакция y(n) не зависит от будущих значений воздействия X(n). Иначе говоря, реакция не может возникнуть раньше воздействия.

-стационарны. Это означает, что

-реакция y(n) не зависит от момента подачи воздействия x(n), т.е.

задержанному на n0 воздействию x(n n0 ) соответствует реакции y(n n0 ) .

Это возможно в том случае, когда коэффициенты передаточной функции (разностного уравнения) являются постоянными, не зависящими от времени.

Цифровые фильтры могут быть реализованы аппаратно, программно и аппаратно-программно.

Аппаратная реализация подразумевает использование разнообразных блоков (регистров, сумматоров, умножителей, устройств памяти, логических элементов и т.п.), объединяемых в единое устройство.

Программная реализация означает, что фильтр представлен в виде программы, написанной на языке высокого уровня (для компьютеров), либо на языке соответствующего ассемблера (для микропроцессорного комплекта).

Аппаратно-программная реализация говорит о том, что часть функций фильтра выполняется аппаратно (АЦП, ЦАП, синхронизация, приѐм/передача данных), а другая часть функций выполняется программно.

9.2 СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ

Под синтезом понимают этап проектирования ЦФ, результатом которого является функциональная схема фильтра с коэффициентами. Каждый из классов ЦФ (КИХ и БИХ) имеют свои, принципиально отличные методы синтеза, однако имеют одинаковую последовательность действий:

-задание требований к фильтрам;

-решение задачи аппроксимации характеристик фильтра, в

результате которой рассчитывается коэффициенты передаточной функции (разностного уравнения); - конструирование функциональной схемы ЦФ.

По наличию аналогового прототипа различают:

-методы синтеза с использованием аналогового прототипа;

-прямые (без использования аналогового прототипа) методы синтеза.

87

9.2.1 Требования цифровым фильтрам

Требования к фильтрам могут формироваться как во временной (рис. 9.2, а), так и в частотной областях (рис. 9.2, б), что определяется назначением фильтра и областью его описания.

Во временной области требования могут задаваться к импульсной h(n) или переходной g(n) характеристикам.

В частотной области обычно синтезируются избирательные фильтры. При этом требования могут предъявляться только к АЧХ , только ФЧХ, либо одновременно к АЧХ и ФЧХ.

9.2.2Задание требований к цифровым фильтрам на примере избирательных фильтров

Рассмотрим требования, предъявляемые к АЧХ и характеристикам ослабления (затухания) избирательных фильтров. Все требования отображаются на диаграммах. Идеальную АЧХ обозначим ( f ) .

Фильтр нижних частот (ФНЧ) имеет три частотных полосы (рис. 9.3 б), полосу пропускания (ПП), полосу задержки (ПЗ), или полосу ослабления (рис. 9.3 в) и затухания (рис. 9.3 г) и переходную полосу.

Полоса пропускания (ПП) ограничивается частотой среза f x ; ширина полосы пропускания fПП fx ;

1 - максимально допустимое отклонение от 1 (рис. 9.3 б) в полосе пропускания.

Важным является то обстоятельство, что в соответствии с методом синтеза КИХ фильтров отклонение АЧХ от 1 задаѐтся симметрично 1 1 A( f ) 1 1 , а для БИХ фильтров отклонение задаѐтся только в одну сторону так, чтобы АЧХ не превышала единицы, что отображено на рис. 9.3 б вынесенной диаграммой.

Полоса задерживания (ослабления) лежит в пределах от граничной

частоты	fk до половины частоты		дискретизации f Д 2 . Еѐ ширина
fПЗ f Д	2 fk .
2 - максимально допустимое отклонение от 0.
	x(n)					y(n)
		h(n), g(n)
		а)
	x(n)					y(n)
		ˆ	ˆ	ˆ
		A( ), a( ),		( )

б)

88

Рисунок 9.2

1

а)

f x f Д 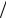2

1 1
1
1 1		БИХ	1	2 1КИХ
	Полоса	Полоса
		задерживания
	пропускания

2	б)
f	f x f Д 2
Переходная
полоса
Рисунок 9.3 Диаграмма требований к ФНЧ
а) идеальная АЧХ;	б) требование к АЧХ

Переходная полоса располагается между полосами пропускания и задержки, еѐ ширина f fk f . Поскольку в этой полосе требования не

задаются, удовлетворительным окажется любое решение, если оно соответствует требованиям в полосах пропускания и задерживания.

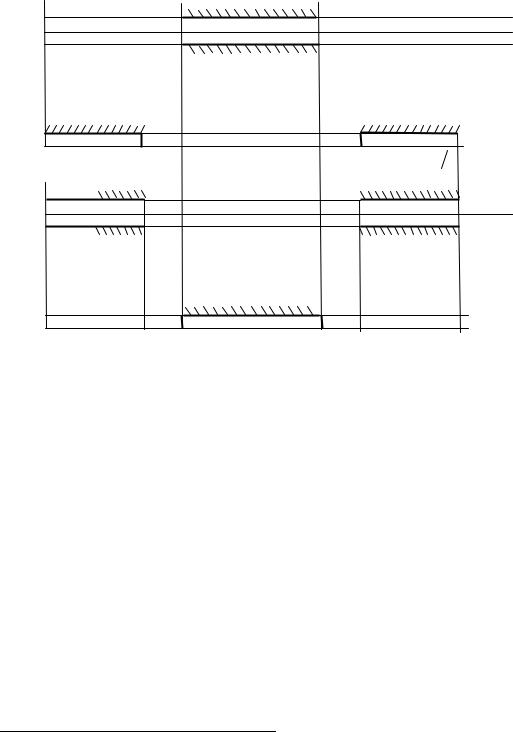
Аналогичные диаграммы требований можно составить к фильтру верхних частот (рис. 9.4) (ФВЧ), полосовому фильтру (ПФ) (рис. 9.5) и режекторному фильтру (РФ) (рис. 9.6)

А(f)

1 1

1 1

					ПП
		ПЗ
	2			f	f Д 2
		fk				f

Рисунок 9.4 Диаграмма требований к ФВЧ

89

f Д 2

1 11

1 1

		ПП
ПЗ1			ПЗ2
2			а)
f k	f	f f k	f Д 2

1 11 1 1

	ПП	ПП2
2		б)

Рисунок 9.5

9.2.3 Характеристика задачи оптимального синтеза

Типовой, весьма распространенной задачей оптимального синтеза является получение цифрового фильтра минимального порядка при условии достижения наилучшего воспроизведения (наилучшей аппроксимации) требуемой АЧХ при заданных ограничениях.

Преследуемая цель формально может быть выражена как функция одного или нескольких аргументов, которую требуется минимизировать (или максимизировать). Минимизируемая (максимизируемая) функция называется ЦЕЛЕВОЙ: ею определяется качество достижения поставленной цели. К примеру, степень полученного воспроизведения АЧХ оценивается допустимым отклонением 1 в полосе пропускания фильтра.

Однако достижение определѐнного цели зависит от КРИТЕРИЯ ОПТИМАЛЬНОСТИ (например минимакс, СКО и т.п.)

Критерием оптимальности называют показатель, который характеризует общую ценность и включается в постановку задачи.

При решении поставленных задач необходимо учитывать существующие ограничения (например, непревышение АХ единицы для БИХ фильтров). Любое решение, удовлетворяющее заданным ограничениям, называется допустимым.

Чаще всего при конструировании передаточной функции H(z) в качестве критерия оптимальности используется мера близости ρ реальной АЧХ A(f) к желаемой ( f ) .

90