1.7.2. Соотношения между множителями подобного преобразования и получение критериев подобия

Условия гидродинамического подобия. Здесь должны быть рассмотрены условия, при которых в геометрически подобных системах осуществляются подобные движения потоков жидкости. Жидкость будем считать ньютоновской и несжимаемой.

Пусть имеются две подобные между собой системы. Все величины, относящиеся к первой из них, будем обозначать буквами без штрихов, а величины второй системы – теми же буквами со штрихом. Гидродинамические условия потока описываются уравнениями движения и сплошности Ограничиваясь рассмотрением неразрывных сред, проанализируем лишь уравнения движения потоков. Последние для простоты выкладок будем писать лишь в виде проекций сил на ось z. Тогда для первой системы

.

Для стационарных процессов, которые и будут далее рассматриваться, и уравнение может быть упрощено:

. (А)

Аналогично для второй системы

. (В)

Поскольку рассматриваемые процессы подобны, отношения одноименных величин в сходственных точках для них одинаковы и имеют следующие значения:

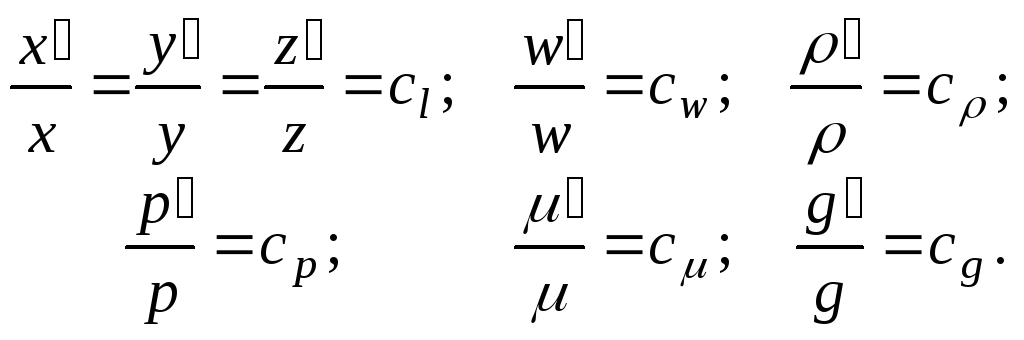
С помощью множителей подобного преобразования c_l,с_w,с_и т. д. выразим переменные второй системы через переменные первой:

Подставляя полученные значения в уравнение (В) и вынося за скобку одноименные множители подобного преобразования, получим

. (С)

Теперь уравнения движения обеих систем (А) и (С) записаны через переменные первой системы. Очевидно что из этих уравнений одноименные переменные должны быть получены одинаковыми. Это возможно только при тождественности уравнений (А) и (С). Для этого необходимо, чтобы комплексы, составленные из множителей подобного преобразования, сократились, т. е. чтобы

. (D)

Таким образом, для гидродинамически подобных потоков множители подобного преобразования не могут быть выбраны произвольно, а должны находиться из соотношений, определяемых выражением (D). Указанные соотношения целесообразно выразить через величины, непосредственно входящие в уравнение движения. Для этого рассмотрим соотношения (D) попарно. Из равенства комплексов (а) и (б) получим, или.

После подстановки значений множителей подобного преобразования имеем 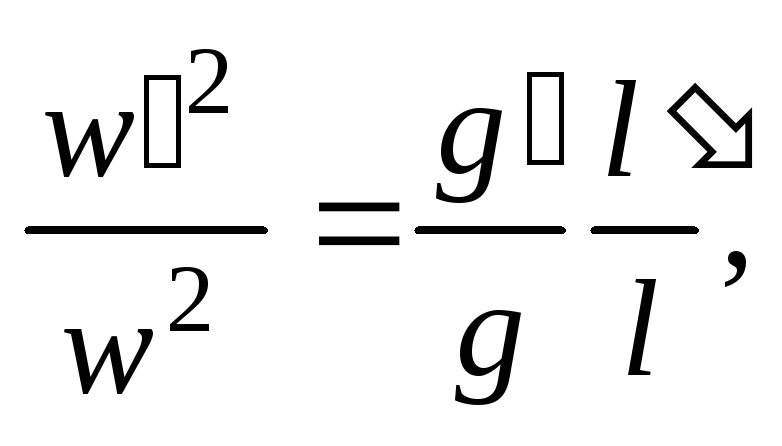или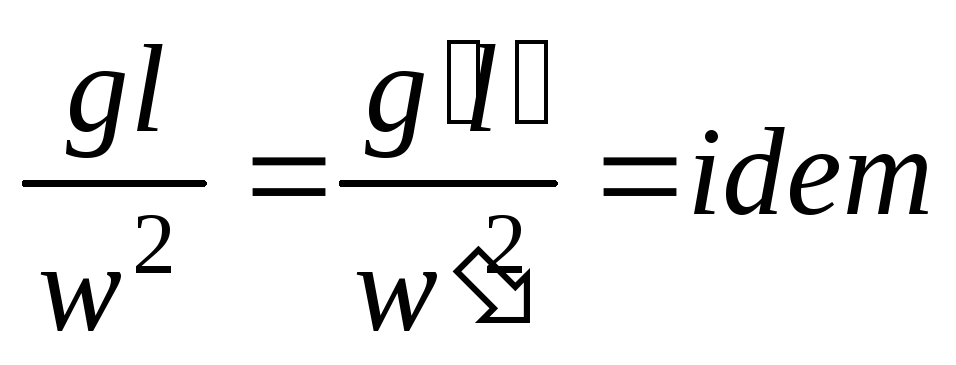(idem–одно и то же).

Полученный комплекс, одинаковый для рассматриваемых подобных явлений и имеющий нулевую размерность, назван критерием Фруда:

.

При его получении сопоставлялись левая часть уравнения движения, отображающая силу инерции, и первое слагаемое правой части, отображающее силу тяжести. Соответственно критерий подобия Fr характеризует соотношение сил инерции и тяжести при вынужденном движении жидкости.

Если далее рассмотреть равенство комплексов (а) и (в) соотношения (D), то можно получить:

, или;, или.

Комплекс назван критерием Эйлера:

.

Анализируя его вывод из уравнения (A), можно видеть, что критерий Эйлера характеризует соотношение сил инерции и давления при вынужденном движении.

Аналогично предыдущему, рассматривая равенства (а) и (г), имеем:

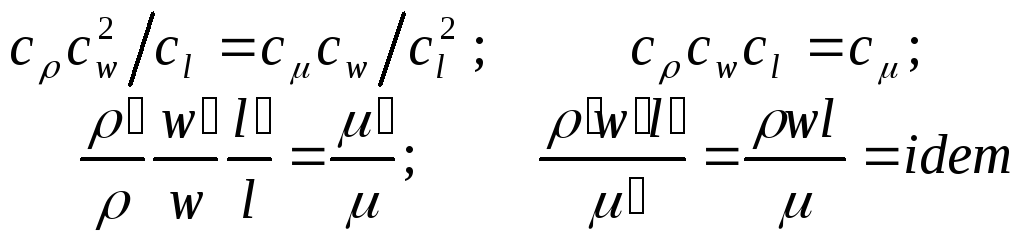
(здесь и ранее под lиl'понимаются любые сходственные геометрические размеры систем).

Комплекс назван критерием Рейнольдcа:, или, поскольку,

.

Очевидно, что этот критерий характеризует соотношение сил инерции и внутреннего трения (вязкости) при вынужденном движении среды. Следовательно, при гидродинамическом подобии двух или нескольких потоков для любых сходственных точек критерии подобия Fr, Eu и Re имеют одни и те же значения.

Критерии подобия можно видоизменять, рассматривая их совместно в целях приведения к виду, наиболее удобному для описания конкретных задач. Так, при исследовании движения, вызываемого различной плотностью отдельных частиц жидкости без перемещения всего ее объема внешним источником движения, скорость потока не может быть измерена, и поэтому критерии Fr и Re не могут быть определены. В этом случае удобнее их так скомпоновать, чтобы выделить новый критерий, в который входила бы разность плотностей отдельных частиц (слоев) жидкости, являющаяся причиной движения, а скорость потока была бы исключена. Для этого умножают Fr на Re²и на относительную разность плотностей потокагдеи₀– плотности различных частиц (слоев) жидкости:

.

Полученный безразмерный комплекс

называют критерием Архимеда.