
- •Министерство образования и науки Российской Федерации
- •Введение
- •Измерения в экономике
- •Глава 1. Простой корреляционный и регрессионный анализ
- •Коэффициент парной корреляции
- •1.2. Парная (простая) линейная регрессия
- •1.2.1. Метод наименьших квадратов (мнк) и его предпосылки
- •1.2.2. Оценки точности уравнения регрессии и его параметров
- •1.3.2. Проверка остатков регрессии на автокорреляцию (статистика Дарбина – Уотсона)
- •Глава 2. Множественная корреляция и регрессия
- •2.1. Множественный корреляционный анализ
- •2.1.1. Анализ матрицы парных коэффициентов корреляции
- •2.1.2. Частная и множественная корреляция
- •2.2. Множественный регрессионный анализ
- •2.2.1. Метод наименьших квадратов и его предпосылки
- •2.2.2 Свойства мнк-оценок
- •2.2.3. Показатели точности уравнения регрессии и оценок его параметров
- •2.2.4. Мультиколлинеарность
- •2.2.5. Тестирование предпосылок мнк для множественной регрессии Анализ остатков уравнения множественной регрессии на автокорреляцию
- •Тестирование остатков на гомоскедастичность
- •Тестирование ошибки спецификации уравнения регрессии
- •2.2.6. Учёт некоторых нарушений стандартных предположений о модели
- •2.2.7. Обобщённый метод наименьших квадратов
- •2.2.8. Стандартизованное уравнение множественной регрессии
- •2.2.9. Дискретные переменные в регрессионном анализе
- •2.2.10. Дискретные (качественные) зависимые переменные
- •2.2.11. Пошаговый регрессионный анализ
- •Глава 3. Стохастические объясняющие переменные в регрессионном анализе
- •3.1. Инструментальные переменные
- •3.2. Системы одновременных уравнений
- •3.2.1. Оценивание параметров системы одновременных уравнений
- •Библиографический список
- •Оглавление
- •Глава 1. Простой корреляционный и регрессионный анализ……………… 5
- •Глава 2. Множественная корреляция и регрессия………………………… 23
- •Глава 3. Стохастические объясняющие переменные
- •Учебное издание
Глава 1. Простой корреляционный и регрессионный анализ
Коэффициент парной корреляции
Корреляционным анализом называется совокупность статистических приемов, с помощью которых исследуются и обобщаются взаимосвязи корреляционно связанных величин.
В эконометрике корреляционный анализ применяется для выявления наличия или отсутствия зависимостей между анализируемыми признаками. И только после утвердительного ответа на этот вопрос имеет смысл определять вид зависимости. В дальнейшем в основном будем иметь дело со случайными величинами, следующими нормальному закону распределения, поэтому, если не будет особо оговорено, будем говорить о линейной зависимости.
Меру линейной зависимости между величинами Y и X определяют с помощью ковариации. Она определяется как
 =
cov(Y,X) = M{(Y-
=
cov(Y,X) = M{(Y- )(X-
)(X- )},
)},
где
 и
и – соответственно, математические
ожиданияY
и X.
Таким образом, ковариация между случайными
переменными – это математическое
ожидание произведения отклонений
значений случайных переменных от их
математических ожиданий. Если X
= Y,
то имеем дисперсию случайной величины
X,
т. е.
– соответственно, математические
ожиданияY
и X.
Таким образом, ковариация между случайными
переменными – это математическое
ожидание произведения отклонений
значений случайных переменных от их
математических ожиданий. Если X
= Y,
то имеем дисперсию случайной величины
X,
т. е.
 =
=
 =M{(X-
=M{(X- )2}.
)2}.
Корень
квадратный из дисперсии называется
стандартным отклонением и обозначается
как
 .
Если известно, о какой переменной идёт
речь, то нижний индекс у стандартного
отклонения и дисперсии обычно не
ставится.
.
Если известно, о какой переменной идёт
речь, то нижний индекс у стандартного
отклонения и дисперсии обычно не
ставится.
Чем больше величина ковариации, тем теснее линейная связь между переменными. Но с этой характеристикой не совсем удобно работать, т. к. её величина зависит от единиц измерения анализируемых показателей. Чтобы избавиться от этого недостатка, ковариацию стандартизируют двумя стандартными отклонениям, получая при этом коэффициент корреляции, т. е.
 =
=
 .
.
Коэффициент
корреляции всегда лежит между –1 и +1 и
не зависит от масштаба переменных. Если
ковариация cov(Y,X)
= 0, то говорят, что случайные переменные
некоррелированны, т. е. между ними
отсутствует линейная зависимость. То
же самое можно говорить и о коэффициенте
корреляции. Если случайные величины
статистически независимы, то
 = 0, а в случае нормального распределения
из их некоррелированности, когда
= 0, а в случае нормального распределения
из их некоррелированности, когда = 0, следует их независимость. Две случайные
переменныеY
и X
коррелированы полностью (
= 0, следует их независимость. Две случайные
переменныеY
и X
коррелированы полностью ( = 1), еслиY
= aX
для некоторого положительного значения
a.
= 1), еслиY
= aX
для некоторого положительного значения
a.
Далее будем пользоваться свойствами дисперсии и ковариации, из которых следует, что дисперсия суммы двух некоррелированных переменных равна сумме дисперсий этих переменных, а ковариация двух переменных равна математическому ожиданию произведения этих переменных, если математическое ожидание хотя бы одной из них равно нулю.
Покажем
последнее. Пусть
 = 0. Тогдаcov(Y,X)
= M{(Y
–
= 0. Тогдаcov(Y,X)
= M{(Y
–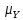 )(X
–
)(X
– )}
= =M{(Y
–
)}
= =M{(Y
– )(X)}
= M{(YX)
–
)(X)}
= M{(YX)
– X)}
= M{(YX)
– M
X)}
= M{(YX)
– M X)}
= M{(YX)
–
X)}
= M{(YX)
– (X)}=
= M{(YX)}–
(X)}=
= M{(YX)}– =M{(YX)}.
Т. е. в нашем случае cov(Y,X)
=
M{(YX)}.
=M{(YX)}.
Т. е. в нашем случае cov(Y,X)
=
M{(YX)}.
До сих пор рассуждения велись по отношению к параметрам генеральной совокупности. Исследователь обычно работает с выборками, на основе которых получает приближённые значения параметров. Эти приближённые значения называют оценками параметров. Для того чтобы оценки были «хорошими», необходимо, чтобы они были несмещёнными, эффективными и состоятельными.
Оценка называется несмещённой, если её математическое ожидание равно самому оцениваемому параметру. Несмещённость оценки означает, что она в среднем соответствует оцениваемому параметру.
Оценка называется эффективной, если она обладает наименьшей дисперсией среди всех альтернативных оценок.
Оценка называется состоятельной, если при увеличении объёма выборки оценка сходится к оцениваемому параметру.
Так,
известно, что выборочная средняя
арифметическая является несмещённой
оценкой генеральной средней. В дальнейшем
оценку параметра будем обозначать той
же буквой, что и параметр, но сверху
будем помечать её знаком «крышки». Тогда
можно записать, что
 =
= ,
где
,
где – выборочная средняя арифметическая.
А выборочная дисперсия – смещённая
оценка генеральной дисперсии и первую
приходится подправлять, вводя поправочный
коэффициент. Так, если выборочную
дисперсию обозначить черезS2,
то несмещённой оценкой генеральной
дисперсии будет
– выборочная средняя арифметическая.
А выборочная дисперсия – смещённая
оценка генеральной дисперсии и первую
приходится подправлять, вводя поправочный
коэффициент. Так, если выборочную
дисперсию обозначить черезS2,
то несмещённой оценкой генеральной
дисперсии будет
 2
=
2
=
 S2.
S2.
Оценкой коэффициента корреляции генеральной совокупности является выборочный коэффициент корреляции, определяемый из соотношения
 =
=
 =
= =
=
где в числителе стоит выборочная ковариация, а в знаменателе – произведение выборочных стандартных отклонений.
Поскольку
речь здесь идёт об оценке, а оценка –
величина случайная, то необходимо
проверить её надёжность. Осуществляется
это с помощью проверки гипотезы о том,
что коэффициент корреляции генеральной
совокупности равен нулю. Итак, нулевая
гипотеза H0
:
 = 0, альтернативнаяHa
:
= 0, альтернативнаяHa
:

 0.
0.
Проверяются статистические гипотезы по стандартному алгоритму. Сначала по выборочным данным вычисляется статистика, закон распределения которой известен, если верна нулевая гипотеза. Затем по фиксированному уровню значимости и известному числу степеней свободы определяются критические точки данного распределения. По критическим точкам определяется область принятия гипотезы и критическая область. Если вычисленное значение статистики попало в область принятия гипотезы, то нулевая гипотеза не отклоняется. В противном случае – отклоняется.
В нашем случае рассчитывается t-статистика вида
t
=
 .
.
Известно,
что если верна нулевая гипотеза, т. е.
если
 = 0, то эта статистика следует распределению
Стьюдента с (n–2)
степенями свободы. Зафиксировав уровень
значимости
= 0, то эта статистика следует распределению
Стьюдента с (n–2)
степенями свободы. Зафиксировав уровень
значимости
 (обычно его принимают равным 0,05),
определяем критические точки (
(обычно его принимают равным 0,05),
определяем критические точки ( )
и по ним строим область принятия гипотезы:
(
)
и по ним строим область принятия гипотезы:
( ;+
;+ Если вычисленное значениеt-статистики
попало в эту область, то говорят, что
коэффициент корреляции незначимо
отличен от нуля и линейная зависимость
между анализируемыми переменными
отклоняется. Критические точки обычно
определяются по таблице критических
значений распределения Стьюдента.
Если вычисленное значениеt-статистики
попало в эту область, то говорят, что
коэффициент корреляции незначимо
отличен от нуля и линейная зависимость
между анализируемыми переменными
отклоняется. Критические точки обычно
определяются по таблице критических
значений распределения Стьюдента.
При
компьютерных расчётах обычно вычисляется
расчётный уровень значимости (их в
статистических пакетах обозначают
по-разному: p-value,
p-level,
sign,
Prob.
и т. д.), это вероятность того что
 .
Т. е.p-value
= P(
.
Т. е.p-value
= P( ).
Грубо говоря, это вероятность того, что
вычисленное значениеt-статистика
попало в область принятия гипотезы.
Расчётный уровень значимости сравнивают
с принятым уровнем значимости (у нас
это
).
Грубо говоря, это вероятность того, что
вычисленное значениеt-статистика
попало в область принятия гипотезы.
Расчётный уровень значимости сравнивают
с принятым уровнем значимости (у нас
это
 )
и, еслиp-value
)
и, еслиp-value ,
то H0
отклоняется и считается, что переменные
x
и y
коррелированы, Если p-value
,
то H0
отклоняется и считается, что переменные
x
и y
коррелированы, Если p-value ,
то H0
не отклоняется и считается, что переменные
не коррелированы.
,
то H0
не отклоняется и считается, что переменные
не коррелированы.
Если
расчётный уровень значимости близок к
 ,
то при принятии решения рекомендуется
проверять, выполняется ли неравенство
,
то при принятии решения рекомендуется
проверять, выполняется ли неравенство .
.
Для качественной интерпретации значений коэффициентов парной линейной корреляции (в случае их значимого отличия от нуля) можно использовать шкалу Чеддока:
|
Величина коэфф. |
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
|
Характеристика силы связи |
слабая |
Уме-ренная |
заметная |
высокая |
весьма высокая |
