1.2. Парная (простая) линейная регрессия

После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с помощью регрессионного анализа.

Корреляционная зависимость между двумя переменными – это функциональная зависимость между одной переменной и ожидаемым (условным средним) значением другой. Уравнение такой зависимости между двумя переменными называется уравнением регрессии. В случае, если переменных две (одна зависимая и одна независимая), то регрессия называется простой, а если их более двух, то множественная. Если зависимость между переменными линейная, то регрессия называется линейной, в противном случае – нелинейной.

Рассмотрим подробно простую линейную регрессию. Модель такой зависимости может быть представлена в виде

y = α + βx + ε, (1.1)

где у – зависимая переменная (результативный признак);

х – независимая переменная (факторный признак);

α – свободный член уравнения регрессии или константа;

β – коэффициент уравнения регрессии;

ε – случайная величина, характеризующая отклонения фактических значений зависимой переменной у от модельных или теоретических значений, рассчитанных по уравнению регрессии.

При этом предполагается, что объясняющая переменная х – величина не случайная, а объясняемая y – случайная. В дальнейшем это предположение можно будет убрать.

1.2.1. Метод наименьших квадратов (мнк) и его предпосылки

α и β – это параметры модели регрессии (1.1), которые должны быть оценены на основе выборочных данных. На основе этих же выборочных данных должна быть оценена дисперсия ε. Одним из методов вычисления таких оценок является классический метод наименьших квадратов (МНК). Суть МНК состоит в минимизации суммы квадратов отклонений фактических значений зависимой переменной у от их условных математических ожиданий , определяемых по уравнению регрессии:=α + βx, в предположении, что математическое ожидание ε равно нулю. Математическое ожидание y обозначим через, а сумму квадратов отклонений черезQ(.

Q(==.

Здесь суммирование ведётся по всей генеральной совокупности. Данную сумму называют остаточной суммой квадратов.

Чтобы минимизировать эту функцию по параметрам обратимся к условиям первого порядка, полученным дифференцированиемQ() по

= –2),

= –2).

Далее пусть для оценки параметров модели (1.1) организована выборка, содержащая n пар значений переменных (x_i,y_i), где i принимает значения от 1 до n (i=). Приравнивая частные производные к нулю и переходя от генеральной совокупности к выборке (заменив параметры на их оценки), получим систему нормальных уравнений для вычисления оценок параметровα и β. Обозначим эти оценки соответственно как а и b. Получим следующую систему нормальных уравнений

) = 0,

) = 0.

Если оценённое уравнение обозначить как y = a + bx + e, где е – одна из реализаций случайной величины ε, соответствующая конкретной выборки, то выражение в скобках системы нормальных уравнений есть не что иное, как остаток уравнения регрессии е_i = y_i и тогда первое уравнение этой системы примет вид 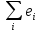= 0. То есть среднее значение остатков равно нулю. Таким образом, если уравнение регрессии содержит константу, то сумма остатков в оценённом уравнении всегда равна нулю.

Второе уравнение системы в этих обозначениях даёт = 0, т. е. векторы значений независимой переменной и остатков ортогональны (независимы).

Приведём один из вариантов формул для вычисления таких оценок:

a = – b, b = . (1.2)

Известно также, что несмещённой оценкой дисперсии случайных отклонений является остаточная дисперсия, вычисляемая из соотношения:

= .

Итак, оценённая модель линейной парной регрессии имеет вид

y = a + bx + e, (1.3)

где е – наблюдаемые отклонения фактических значений зависимой переменной у от расчётных , которые рассчитываются из соотношения=a + bx.

Различие между ε и е состоит в том, что ε – это случайная величина и предсказать её значения не представляется возможным, в то время как е – это наблюдаемые значения отклонений (е = у –) и эти отклонения можно считать случайной выборкой из совокупности значений остатков регрессии и их можно анализировать с использованием статистических методов.

Как было отмечено, МНК строит оценки регрессии на основе минимизации суммы квадратов отклонений или остатков ε, поэтому важно знать их свойства. Для получения «хороших» МНК-оценок необходимо, чтобы выполнялись следующие основные предпосылки относительно остатков модели (1.1), называемые предположениями Гаусса – Маркова.

1. М(ε_i) = 0, (i = 1,…,n);

2. (,…,) независимы;

3. D() =, (i = 1,…,n);

4. Cov() = 0, (i,j = 1,…,n), i.

Первое предположение говорит о том, что математическое ожидание регрессионных остатков равно нулю и подразумевает, что в среднем, линия регрессии должна быть истинной. Предположение 3 утверждает, что все регрессионные остатки имеют одну и ту же дисперсию, и называется предположением гомоскедастичности, а предположение 4 исключает любую форму автокорреляции между ними, т. е. подразумевает нулевую корреляцию между различными регрессионными остатками. Вместе взятые эти предположения означают, что регрессионные остатки являются некоррелированными извлечениями из генеральной совокупности с распределением, имеющем нулевое математическое ожидание и постоянную дисперсию .

Предположение 2 утверждает независимость векторов значений независимой переменной и регрессионных остатков.

Известно, что если выполняются эти четыре предположения, то верна теорема Гаусса – Маркова, утверждающая, что в этом случае МНК-оценка b является наилучшей линейной несмещённой оценкой параметра β. Наилучшей в смысле эффективности.

Кроме сформулированных предположений вводится ещё одно, которое позволило бы сформулировать показатели точности уравнения регрессии и его оценок. Эта предпосылка утверждает, что остатки должны следовать нормальному закону распределения с нулевым математическим ожиданием и постоянной дисперсией.

В дальнейшем уравнение =a + bx будем называть выборочным уравнением регрессии или просто уравнением регрессии, а его коэффициенты, соответственно, свободным членом (а) и коэффициентом уравнения регрессии (b).

Свободный член уравнения регрессии обычно не интерпретируется. Коэффициент регрессии показывает, насколько в среднем изменится зависимая переменная (в своих единицах измерения) при изменении независимой переменной на единицу своего измерения.

При этом, необходимо иметь в виду, что рассматриваемые коэффициенты являются оценками параметров уравнения регрессии =α + βx со всеми вытекающими отсюда последствиями, в том числе и необходимостью получения оценок точности уравнения регрессии и его параметров.

Рассмотрим некоторые из них.