kurs_lekcii_mo_matematicheskomu_analizu / Комплексные числа

ТЕМА 16. КОМПЛЕКСНЫЕ ЧИСЛА.

1.Основные определения

Комплексное число является обобщением понятия вещественного числа. Для построения множества комплексных чисел рассмотрим на плоскости прямоугольную (декартову) систему координат xOy , в которой каждая точка плоскости характеризуется парой чисел (a, b) , где a и b координаты этой точки. Точку (a, b) мы также трактуем как вектор с началом в центре O системы координат и с концом в точке (a, b) . Обозначим на оси Ox вектор единичной длины через ~e , а вектор единичной длины на оси Oy через i . Тогда любой вектор z = (a, b) на плоскости можно представить в виде

z = a · ~e + b · i.

(1)

Заметим, что ~e = (1, 0) , i = (0, 1) . Если вложить вещественную прямую в плоскость в виде координатной оси Ox , т. е. каждому вещественному числу x сопоставить вектор (x, 0) плоскости, то окажется, что все векторы вида z = a · ~e + 0 · i можно трактовать как вещественные числа и потому написание ~e лишнее. Следовательно, каждую точку (вектор) плоскости можно записать в виде

z = a + bi = a + ib.

(2)

Сложение векторов, записанных в виде (2), осуществляется в соответствии с правилом параллелограмма: если z1 = a1 + ib1 , z2 = a2 + ib2 , то

z1 + z2 = (a1 + a2) + i(b1 + b2).

(3)

Введем понятие умножения векторов. Основным положением для этого мы примем следующее: i2 = −1 . Это означает, что (0 + i · 1)2 = −1 + i0 . Для умножения любых векторов мы будем исходить из обычного правила умножения двух двучленов с учетом указанного положения:

z1 · z2 = (a1 + ib1)(a2 + ib2) = a1a2 + ib1 a2 + ia1b2 − b1b2 =	(4)
= (a1a2 − b1b2) + i(b1 a2 + a1b2).

Определение 1. Векторы, записанные в виде (2), называются комплексными числами, на которых определены операции сложения (3) и умножения (4). Для комплексного числа z = a + ib число a называется вещественной частью, b мнимой частью, при этом пишут a = z , b = z .

Два комплексных числа равны тогда и только тогда, когда равны их вещественные, а также мнимые части: если

z1 = a1 + ib1 , z2 = a2 + ib2,

то равенства

z1 = z2 и	b1	= b2,
	a1	= a2,

1

равносильны. Комплексное число равно нулю тогда и только тогда, когда равны нулю его вещественная и мнимая части.

Операция деления комплексных чисел определяется как операция, обратная

умножению. А именно, если z2 6= 0 , то z1/z2	есть такое число z , что z · z2 = z1 . Пусть
zj = aj + ibj , j = 1, 2 , z = a + ib , тогда
(a + ib)(a2 + ib2) = (aa2 − bb2) + i(ba2 + ab2) = a1 + ib1
b2a + a2b	= b1.
aa2 − b2b	= a1,

Эта система линейных уравнений имеет единственное решение, поскольку её определитель

			a2 −b2		= a22	+ b22	= 0,
		b2 a2					6
ибо z2									z1/z2 . На практике эту
		. Решая эту систему, получим выражение для z
	= 0							=
	6

систему не решают, а поступают следующим образом. Введем понятие сопряженного числа к комплексному числу w = x + iy . А именно, сопряженное к w это число

w¯ = x − iy.

Так, для выполнения деления поступим следующим образом:

z =

z1

=

a1 + ib1

z¯2

=

(a1 + ib1)(a2 − ib2)

=

z2

a2 + ib2

· z¯2

(a2 + ib2)(a2

−

ib2)

(a1a2 + b1b2) + i(a2b1 − a1b2)

=

a1a2 + b1b2

+ i

a2b1 − a1b2

.

a22 + b22

a22 + b22

a22 + b22

Пример 1. Выполнить деление

1 + i .

1 − i

Решение. Для этого домножим числитель и знаменатель на число, сопряженное к 1 −i ,

т.е. на 1 + i :

1

+ i

=

(1 + i)(1 + i)

=

1 + 2i − 1

= 0 + i

·

1 = i.

1

i

(1

i)(1 + i)

−

−

2

Пример 2. Выполнить деление

3

+ 2i

.

2

+ 3i

Решение. Домножим числитель и знаменатель на число, сопряженное к 2 + 3i , т.е. на

2 − 3i .
	3 + 2i	=	(3 + 2i)(2 − 3i)	=	6 − 5i + 6	=	12	−	5	i.
	2 + 3i		4 + 9		13		13		13
Кроме алгебраической формы записи z = a + ib комплексного числа z существует

еще одно важное представление, а именно, тригонометрическая форма записи. Заметим,
что каждый вектор (a, b) характеризуется	своей длиной ̺ =			√		и углом ϕ
					a2 + b2
относительно оси Ox , причем угол ϕ определяется из условия
tg ϕ =		b	.
		a

2

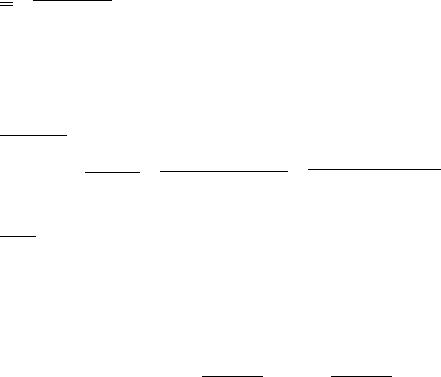
Ясно, что a = ̺ cos ϕ , b = ̺ sin ϕ , поэтому
		z = ̺(cos ϕ + i sin ϕ)			(5)
есть тригонометрическая форма записи комплексного числа z .
Число ̺ = √		называется модулем, а		аргументом комплексного числа
	a2 + b2		ϕ
z = a + ib , при этом используется обозначение			̺	= |z| ,	ϕ = arg z . Модуль любого

комплексного числа имеет вполне определенное значение, тогда как аргумент определен с точностью до целого числа полных оборотов; например: |i| = 1 , Arg i = π2 + 2kπ (k = 0, ±1, ±2, · · ·) . Здесь под Arg понимается общее значение аргумента, составленное с учетом возможности любого числа полных оборотов; в отличие от этого главное значение аргумента argz берется в интервале −180◦ < argz ≤ 180◦ . Числу z = 0 может быть приписан любой аргумент, а модуль этого числа равен нулю. Тригонометрическая форма записи позволяет дать геометрическую интерпретацию операции умножения комплексных чисел. Пусть даны два комплексных числа

z1 = ̺1(cosϕ1 + isinϕ1) и z2 = ̺2(cosϕ2 + isinϕ2).

Тогда

z1 · z2 = ̺1(cosϕ1 + isinϕ1) · ̺2(cosϕ2 + isinϕ2) =

= ̺1̺2(cosϕ1cosϕ2 − sinϕ1sinϕ2) + i̺1̺2(sinϕ1cosϕ2 + cosϕ1sinϕ2) = = ̺1̺2[cos(ϕ1 + ϕ2) + isin(ϕ1 + ϕ2)].

Таким образом, при умножении комплексных чисел их модули умножаются, а аргументы складываются.

В заключение остановимся на некоторых свойствах сопряженных чисел. Рассмотрим комплексное число w = x + iy .

1)w = (x + i(−y)) = x − i(−y) = x + iy = w,

т.е. w и w¯ являются взаимно сопряженными;

2)w + w¯ = 2Rew , w − w¯ = 2iImw ;

3)w = w¯ тогда и только тогда, когда w вещественное;

4)ww¯ = (x + iy)(x − iy) = x2 + y2 = |w|2 ;

5)|w¯| = |w| , Argw¯ = −Argw , т.е. точки w и w¯ симметричны относительно вещественной оси;

6)(w1 + w2) = w¯1 + w¯2 , так как

w1 + w2 = x1 + iy1 + x2 + iy2 = x1 + x2 + i(y1 + y2) =

=x1 + x2 − i(y1 + y2) = (x1 − iy1) + (x2 − iy2) = w¯1 + w¯2;

7)w1w2 = w¯1 · w¯2 , что проверяется аналогично свойству 6◦ .

Замечание 1. Для нахождения аргумента							комплексного числа удобнее
использовать вместо равенства				b
		tgϕ =
				a
пару равенств
		a					b
cos ϕ =	√		, sin ϕ =			√		.
		a2 + b2					a2 + b2

3

−1

−1

Пример 3. Представить z = −1 − i в тригонометрическом виде. Решение. Тогда

√

ρ = 2 , tg ϕ = tg = tg 1 . Запись

z = √2(cos π4 + i sin π4 )

будет ошибочной. Правильно

z = √

2(cos

−3π

+ i sin

−3π

),

4

4

так как

−1

−1

cos ϕ =

, sin ϕ =

.

√2

√2

Иногда главное значение аргумента берут в интервале 0 ≤ arg z < 2π .

2.Формула Муавра. Формула Эйлера

Правило умножения комплексных чисел автоматически распространяется на любое число сомножителей. Если, в частности, взять все сомножители равными, то получаем

[̺(cosϕ + isinϕ)]n = ̺n(cosnϕ + isinnϕ), (n = 2, 3, . . .);

если же положить ρ = 1 , получим формулу

(cosϕ + isinϕ)n = cosnϕ + isinnϕ,

(6)

названную формулой Муавра по имени английского математика А. Муавра, нашедшего ее в 1707 году.

√Переходим к извлечению корня из комплексных чисел. Если z = ̺(cosϕ + isinϕ) дано, а n z = w = r(cosψ+isinψ) ищется, то по определению корня z = wn = rn(cosnψ+isinnψ) . Сравнивая с предыдущим выражением для z , получим

rn = ̺, nψ = ϕ + 2kπ (k любое целое).

Так как				r и ̺ положительные
под (	√		)	понимается “обыкновенный”
		ρ
	n

положительного числа. Таким образом,

числа, то				ϕ+2kπ	,	где
	n
	r = ( √̺) , ψ =			n
(арифметический, положительный)				корень		из

	√		ϕ + 2kπ		ϕ + 2kπ		(7)
w = (		̺	)(cos	+ i sin	).
	n
			n		n

Придавая k значения 0, 1, 2, . . . , мы будем получать возможные значения для корня w1 , w2 , w3 , ... . Однако при k = n получится

wn+1

= (

√

)(cos

ϕ + 2nπ

+ i sin

ϕ + 2nπ

) =

̺

n

n

n

√

ϕ

ϕ

= (

̺

)[cos( n

+ 2π) + i sin( n

+ 2π)] =

n

4

	√		ϕ		ϕ
= (		̺	)(cos n	+ i sin n ) = w1.
	n

Аналогично wn+2 = w2 и т.д.; при отрицательных k также не будет ничего нового: при k = −1 получится то же, что при k = n − 1 , и т.д.

Окончательно,

				[ p
					̺(cos ϕ + i sin ϕ)]k+1 =
				n
	√			ϕ + 2πk			ϕ + 2πk				(8)
= (		̺	)(cos			+ i sin		), (k = 0, 1, . . . , n	−	1).
				n			n
	n

Итак, мы видим, что корень n –й степени из комплексного числа имеет n различных значений; единственным исключением является число z = 0 , все корни из которого равны

нулю. Пример 4.

Извлечь квадратный корень из комплексного числа

z = 2i = 2(cos

π

+ i sin

π

).

2

2

Решение. По формуле (8) имеем

√

√

π2 + 2kπ

π2 + 2kπ

(

2i)1,2 = ( 2){cos

+ i sin

} (k = 0, 1).

2

2

Первый корень при k = 0 равен

(√

)1 = √

π2 + 2 · 0 · π

π2 + 2 · 0 · π

√

√

+ i

√

) = 1 + i.

2(cos

+ i sin

) =

2

2

2i

2(

2

2

2

2

√

Аналогично, подставив k = 1 , получим второй корень (

2i)2 = −1 − i .

Если

|

z

|

= 1 , ϕ = argz , то по формуле (5) имеем z = cos ϕ+i sin ϕ . Комплексное число

iϕ

iϕ

для любого действительного

cos ϕ + i sin ϕ обозначается символом

e , т.е. функция e

числа ϕ определяется формулой Эйлера:

eiϕ = cos ϕ + i sin ϕ.

(9)

В частности, e2iπ = 1 , eiπ = −1 , eπi/2 = i , e−πi/2 = −i . Отметим, что |eiϕ| = 1 для любого действительного числа ϕ . Из (9) заменой ϕ на −ϕ получается равенство

e−iϕ = cos ϕ − i sin ϕ.					(10)
Сложением и вычитанием равенств (9) и (10) получаются формулы Эйлера:
cos ϕ =	1		(eiϕ + e−iϕ),
		2
sin ϕ =	1			(eiϕ − e−iϕ),	(11)
	2i

с помощью которых тригонометрические функции выражаются через показательную функцию.

5

3.Комплексные функции действительного аргумента

Иногда приходится рассматривать такие функции, у которых независимая переменная вещественна, а сама функция принимает комплексные значения. Примерами могут служить функции

1) z = (t + i)3; 2) z = M ept (p = a + iω) и т. д.;

здесь независимая переменная обозначена буквой t , а функция буквой z . Если разложить значения функции на вещественную и мнимую части, z = x + iy , то каждая из этих частей будет функцией от t . Так в приведенных примерах получим

1)x = t3 − 3t, y = 3t2 − 1; 2)x = M eat cos ωt, y = M eat sin ωt,
где M вещественное.
В общем случае, если
z = f (t) = ϕ(t) + iψ(t),	(12)
то получаем
x = ϕ(t), y = ψ(t);	(13)

можно перейти от (13) к (12). Таким образом, задание комплексной функции от вещественного аргумента равносильно заданию двух вещественных функций от того же аргумента.

Таким образом, теория комплексных функций от вещественного аргумента не имеет существенно новых черт по сравнению с теорией вещественных функций. В частности, определения непрерывности, производной и т. п. переносятся без изменений. При этом все формулы дифференцирования сохраняются, например:

[(t + i)3]′ = 3(t + i)2, (M ept)′ = M pept и т. п.

Изображается функция (12) линией в комплексной плоскости с параметрическими уравнениями (13).

При применении функций вида (12) надо иметь в виду следующие очевидные свойства:

–при сложении комплексных функций их вещественные и мнимые части складываются;

–при умножении на вещественную постоянную или вещественную функцию комплексной функции вещественная и мнимая части получают тот же сомножитель;

–при дифференцировании комплексной функции дифференцируется ее вещественная

имнимая части.

Формулами эти свойства можно записать так:

[f1(t) + f2(t)] = f1(t) + f2(t),

[f1(t) + f2(t)] = f1(t) + f2(t),

[cf (t)] = c f (t),

[cf (t)] = c f (t),

6

здесь c вещественная постоянная,

f ′(t) = ( f (t))′ + i( f (t))′ = ϕ′(t) + iψ′(t).

Эти свойства дают возможность, вместо того чтобы производить указанные действия над вещественной или мнимой частью, осуществить эти действия над всей комплексной функцией, а от результата взять вещественную или соответственно мнимую часть.

Пример 5. Продифференцировать функцию f (t) = M ept ( M вещественное, p = a + iω ). Решение. Вещественная и мнимая части f (x) соответственно равны

ϕ(t) = M eat cos ωt, ψ(t) = M eat sin ωt

(об этом уже говорилось выше). Продифференцируем f (t) :

f ′(t) = M pept.

В полученном результате выделим вещественную и мнимую части:

M pept = M (a + iω)eat(cos ωt + i sin ωt) =

=M eat (a cos ωt + iω cos ωt + ia sin ωt − ω sin ωt) =

=M eat (a cos ωt − ω sin ωt) + iM eat (ω cos ωt + a sin ωt) =

=ϕ′(t) + iψ′(t).

7