8. Теорема Пойнтинга для комплексных амплитуд

Для важного в практическом отношении частного случая, когда поле изменяется во времени по гармоническому закону, вектор Пойнтинга может быть выражен через комплексные амплитуды полей и, поскольку

Здесь индекс * обозначает комплексно сопряженные величины. Подставляя выражения для ив формулу для вектора Пойнтинга, будем иметь

Первое слагаемое в правой части неизменно во времени, а второе изменяется во времени с удвоенной частотой.

Таким образом, процесс переноса энергии в электромагнитном поле, изменяющемся во времени по гармоническому закону, характеризуется, с одной стороны, вещественным вектором

,

равным средней за период плотности мощности излучения, и вещественным вектором

,

который указывает на существование колеблющейся составляющей вектора Пойнтинга. Следует иметь в виду, что среднее за период значение вектора равно нулю.

Ассоциация вектора Пойнтинга с процессом переноса электромагнитной энергии от источника, например, антенны, к любым другим сколь угодно удаленным точкам не всегда верна. Физический опыт и теоретическое рассмотрение на основе уравнений Максвелла позволяют утверждать, что в узком смысле слова термин «излучение» применим лишь к переменным во времени процессам в силу волнового характера распространения электромагнитного поля. Тем не менее, введенный вектор Пойнтинга позволяет правильно описать процесс передачи электромагнитной энергии в системах с неизменными во времени полями. В качестве примера на изображен эскиз двухпроводной линии передачи, в которой энергия от источника постоянной ЭДС передается к резистивной нагрузке.

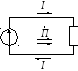
40. − Передача энергии электромагнитного поля от генератора к нагрузке

Из рисунка следует, что в каждой точке пространства может быть построен отличный от нуля вектор Пойнтинга , ориентированный вдоль оси линии передачи от генератора к нагрузке. Если проинтегрировать вектор Пойнтинга по поперечной плоскости в бесконечных пределах, то в результате будет получена величина переносимой мощности, выраженная в электротехнических терминах как произведение напряжения на нагрузке на силу протекающего тока. Вывод, следующий отсюда, может показаться несколько неожиданным: с точки зрения электродинамики, энергия в данной системе переносится не токами, текущими в проводниках, а электромагнитным полем в окружающем пространстве. Наличие проводников и токов в них выступает лишь как необходимое условие существования полей требуемой конфигурации.

5. Лекция 5.

   1. Уравнения Гельмгольца. Волновой характер электромагнитного поля

Одним из важнейших результатов, полученных Максвеллом, явилось доказательство волновой природы электромагнитного поля. Уже упоминалось о том, что изменение во времени электрического поля приводит к возникновению магнитного поля, неоднородного в пространстве, и наоборот. Физическая картина здесь напоминает процесс обмена энергией между электрическим и магнитным полем в обычном колебательном контуре. Поэтому можно ожидать, что электромагнитный процесс в самом общем случае представляет собой также некоторые колебания. Принципиальная разница здесь заключается в том, что колебания электромагнитного поля должны рассматриваться одновременно во всех точках пространства. В физике колебательное движение непрерывной среды принято называть волновым процессом.

Докажем волновой характер электромагнитного поля математически, сведя уравнения Максвелла к другим уравнениям, которые заведомо описывают волновой процесс.

Рассмотрим электромагнитное поле в некоторой области пространства, где плотность зарядов отсутствует, т.е. . Плотность сторонних электрических токов также предполагается равной нулю.

Выпишем первые два уравнения из общей системы уравнений Максвелла для комплексных амплитуд в виде:

Эти два уравнения могут быть сведены к одному. Для этого применим операцию rotк левой и правой частям второго уравнения, а затем выразим полученную правую часть через второе уравнение:

Здесь − в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величиныможно встретить также названия фазовая постоянная или волновое число.

Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождеством векторного анализа:

.

Здесь (набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие операторасводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа

.

Если воспользоваться законом Гаусса, который в соответствии с принятым условием обеспечивает, то уравнение может быть переписано в следующем простом виде:

Пользуясь симметрией уравнений Максвелла, совершенно аналогично получаем также уравнение относительно векторного поля :

.

Эти два уравнения в математической физике носят название уравнений Гельмгольца. Математически можно показать, что эти уравнения описывают стационарные волновые процессы, т.е., распространение в пространстве волн с некоторой постоянной частотой.

Таким образом, получен фундаментальный вывод теории Максвелла − переменность во времени электрических или магнитных полей приводит к распространению в пространстве электромагнитных волн.

В координатной форме уравнения Гельмгольца записываются следующим образом

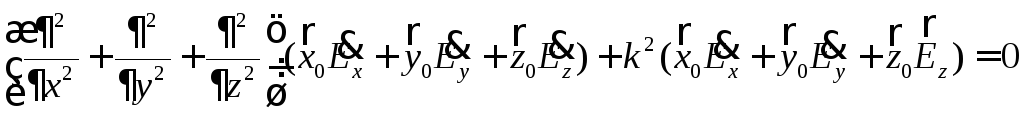
или

.

Решение такой системы значительно упрощается в тех частных случаях, когда поле не имеет каких-либо составляющих, например, , а также тогда, когда поле постоянно в каких-либо плоскостях, например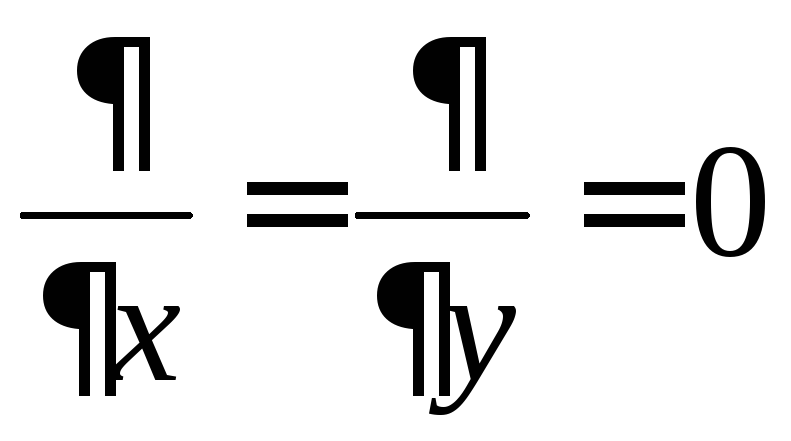.