

p,“. 2.46. q.ем= 3“2=…%"*, дл %C!еделе…, =…,ƒ%2!%C,, Cл=“2=
билизации на каждом режиме фиксируются значения давлений на входе ðâõ и выходе ðâûõ, а также расход газа Q (с помощью расходомера 8). Результаты опытов с образцом песчаной породы в разных направлениях приведены в табл. 2.34. Цикл измерений проведен для восьми уравнений, т.е. для положений образца под углами 0, 45, 90, 135, 180, 225, 270 и 315°, которые фиксировались фиксатором.
Обработка результатов. Результаты, полученные для различных положений образца высокопроницаемой, практически изотропной породы на разных режимах, обрабатывали по двучленной формуле
p2 |
− p2 |
= aQ + bQ 2 , |
(2.256) |
âõ |
âûõ |
|
|
ãäå ðâõ, ðâûõ – давление на входе в образец и на выходе из него, Па; Q – расход газа, м3/ñ.
Коэффициент фильтрационного сопротивления
a = 2LµzpàòÒîï/(FkTñò), |
(2.257) |
где µ – динамическая вязкость, мПа с; L – длина образца, м (в данном случае фильтрация воздуха происходит по параллелограмму); z – коэффициент сверхсжимаемости (в условиях эксперимента принимали z = 1, так как давление газа не превышало 0,243 МПа); Toï, Tñò – температура газа в образце и стандартная температура, (в условиях опыта Òoï = Tcò); F – площадь поперечного сечения образца, м2; k – коэффициент проницаемости, мкм2.
В формуле (2.256)
b = ρàòpàòLzTîï/(F 2 lTñò), |
(2.258) |
ãäå l – коэффициент макрошероховатости.
По результатам, обработанным по формуле (2.256), при определенном угле фильтрации газа для каждого режима построены индикаторные кривые. Для вычисления проницаемости образца в разных направлениях полученные индикаторные кривые обрабатывали в координатах ∆p2/Q – Q и определяли для каждого изучаемого направления образца коэффициенты a è b. Далее
221
Ò à á ë è ö à 2.34
Результаты измерений давлений и расхода газа при разных положениях образца
Номер |
|
|
|
Положение |
|
0/45o |
|
|
|
|
|
|
|
|
Положение |
|
180o/ 225o |
|
|
|
|
|
|
|||||||
5 |
|
|
90o/135o |
|
|
|
|
|
|
|
270o/315o |
|
|
|
|
|||||||||||||||
режима |
ðâõ 10 , Ïà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ðâûõ 105, Ïà |
|
|
Q 10–3, ì3/ñ |
|
∆p2 1010, Ïà2 |
|
|
∆p2/Q |
|
|
ðâûõ 105, Ïà |
|
|
Q 10–3, ì3/ñ |
|
∆p2 1010, Ïà2 |
|
∆p2/Q |
|||||||||
1 |
2,433 |
1,0665/1,0650 |
|
0,3457/0,3481 |
4,7821/4,7853 |
|
13,83/13,75 |
|
1,0662/1,0668 |
|
0,3465/0,3452 |
|
4,7827/4,7815 |
|
13,80/13,85 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0668/1,0642 |
|
0,3581/0,3510 |
|
4,7811/4,7870 |
|
13,35/13,86 |
|
1,0672/1,0637 |
|
0,3589/0,3311 |
|
4,7806/4,7881 |
13,52/14,45 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
2,233 |
1,0580/1,0576 |
|
0,3021/0,2987 |
|
3,8669/3,8676 |
|
12,96/12,96 |
|
1,0582/1,0584 |
|
0,2974/0,3020 |
|
3,8665/3,8655 |
|
13,05/12,80 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0583/1,0567 |
|
0,3137/0,3023 |
|
3,8660/3,8694 |
|
12,32/12,80 |
|
1,0588/1,0560 |
|
0,3043/0,2942 |
|
3,8653/3,8711 |
|
12,70/13,46 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
2,033 |
1,0512/1,0500 |
|
0,2025/0,2510 |
|
3,0281/3,0301 |
|
12,03/12,07 |
|
1,0509/1,0518 |
|
0,2598/0,2555 |
|
3,0286/ 3,0267 |
|
11,66/11,85 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0514/1,0504 |
|
0,2583/0,2546 |
|
3,0276/3,0300 |
|
12,72/11,90 |
|
1,0514/1,0495 |
|
0,2610 |
/0,2358 |
|
3,0275/3,0310 |
|
11,60/12,13 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4 |
1,833 |
1,0450/1,0445 |
|
0,2025/0,2031 |
2,2679/2,2689 |
|
11,20/11,17 |
|
1,0449/1,0454 |
|
0,2073/0,2127 |
|
2,2680/2,2668 |
|
10,94/10,65 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1,0455/1,0447 |
|
|
0,2159/0,2062 |
|
|
2,2669/2,2685 |
|
|
10,49/11,00 |
|
1,0453/1,0443 |
|
0,2119 |
/0,2001 |
|
2,2671/2,2692 |
|
10,70/11,34 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5 |
1,733 |
1,0424/1,0418 |
|
0,1801/0,1786 |
|
1,9164/1,9176 |
|
10,64/10,74 |
|
1,0423/1,0425 |
|
0,1872/0,1878 |
|
1,9169/1,9165 |
|
10,44/10,20 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0425/1,0421 |
|
0,1869/0,1825 |
|
1,9163/1,9170 |
|
10,25/10,50 |
|
1,0429/1,0418 |
|
0,1871/0,1778 |
|
1,9157/1,9178 |
|
10,24/10,78 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6 |
1,633 |
1,0402/1,0391 |
|
0,1564/0,1515 |
|
1,5847/1,5280 |
|
10,13/10,08 |
|
1,0401/1,0402 |
|
0,1583/0,1633 |
|
1,5849/1,5847 |
|
9,99/9,71 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0404/1,0397 |
|
0,1619/0,1563 |
|
1,5848/1,5860 |
|
9,79/10,15 |
|
1,0404/1,0398 |
|
0,1598 |
/0,1569 |
|
1,5847/1,5855 |
|
9,91/10,10 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
7 |
1,533 |
|
1,0381/1,0379 |
|
|
0,1333/0,1315 |
|
|
1,2723/1,2729 |
|
|
9,54/9,68 |
|
|
|
1,038/1,0383 |
|
|
0,1359/0,1386 |
|
|
1,2724/1,2721 |
|
|
9,36/9,18 |
|
|
|||
1,0380/1,0375 |
|
0,1357/0,1332 |
|
1,2726/1,2740 |
|
9,37/9,57 |
|
|
1,0384/1,0380 |
|
0,1370 |
/0,1308 |
|
1,2718/1,2727 |
|
9,28/9,73 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
8 |
1,433 |
1,0366/1,0358 |
|
0,1055/0,1089 |
|
0,9785/0,9806 |
|
9,28/9,06 |
|
|
1,0364/1,0366 |
|
0,1081/0,1118 |
|
0,9789/0,9785 |
|
9,06/8,75 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1,0365/1,0360 |
|
|
0,1116/0,1088 |
|
|
0,9887/0,9790 |
|
|
8,77/9,00 |
|
|
1,0365/1,0363 |
|
0,1138 |
/0,1076 |
|
0,9790/0,9791 |
8,60/9,10 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9 |
1,333 |
1,0350/1,0352 |
|
0,0807/0,0838 |
|
0,7049/0,7053 |
|
8,74/8,42 |
|
|
1,0351/1,0351 |
|
0,0850/0,0871 |
|
0,7055/0,7055 |
|
8,30/8,10 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0350/1,0350 |
|
0,0851/0,0820 |
|
0,7057/0,7059 |
|
8,29/8,60 |
|
|
1,0352/1,0350 |
|
0,0855 |
/0,0828 |
|
0,7053/0,7057 |
|
8,25/8,52 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
10 |
1,233 |
1,034/1,0342 |
|
0,0550/0,0557 |
|
0,4508/0,4507 |
|
8,20/8,09 |
|
|
1,0341/1,0342 |
|
0,0579/0,0593 |
|
0,4509/0,4507 |
|
7,79/7,60 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0342/1,0342 |
|
0,0580/0,0561 |
0,4507/0,4504 |
|
7,77/8,03 |
|
|
1,0342/1,0342 |
|
0,0590 |
/0,0590 |
|
0,4507/0,4507 |
|
7,63/7,64 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
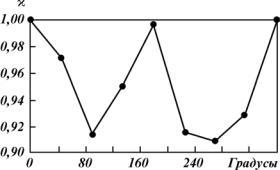
Рис. 2.47. Зависимость параметра анизотропии = kâ/kã от угла поворота образца к направлению напластова-
íèÿ
Š = K ë , ö = 2.35
d=……/å %K!=K%2*, !åƒ3ëü2=2%" %C/2=
|
Направле- |
|
|
|
|
|
Направле- |
|
|
|
|
ние фильт- |
|
|
|
|
|
ние фильт- |
|
|
|
|
рации (угол |
|
|
|
|
|
рации (угол |
|
|
|
¹ ï/ï |
к направле- |
à |
k, ìêì2 |
|
|
¹ ï/ï |
к направле- |
à |
k, ìêì2 |
|
|
нию напла- |
|
|
|
|
|
нию напла- |
|
|
|
|
стования, |
|
|
|
|
|
стования, |
|
|
|
|
градус) |
|
|
|
|
|
градус) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
7,10 |
0,676 |
1,000 |
|
5 |
180 |
7,07 |
0,673 |
0,996 |
2 |
45 |
6,90 |
0,643 |
0,972 |
|
6 |
225 |
6,50 |
0,618 |
0,915 |
3 |
90 |
6,50 |
0,618 |
0,915 |
|
7 |
270 |
6,45 |
0,614 |
0,908 |
4 |
135 |
6,75 |
0,643 |
0,951 |
|
8 |
315 |
6,60 |
0,628 |
0,929 |
|
|
|
|
|
|
|
|
|
|
|
по формуле (2.257) вычисляли коэффициенты проницаемости для различных направлений фильтрации газа (табл. 2.35). Параметр анизотропии определен как отношение a0 ê ai, ò.å.
= ki/k0 = a0/ai. |
(2.259) |
Как следует из характера изменения параметра анизотропии в зависимости от направления фильтрации (рис. 2.47), для рассматриваемого образца максимальная проницаемость получена при угле его поворота по отношению к направлению напластования, равном нулю.
Анализ зависимости проницаемости для разных направлений (см. табл. 2.35) показывает, что при уровнях 0 и 180° значения k практически одинаковы (0,676 и 0,673 мкм2), что соответствует горизонтальному направлению. При 90 и 270° коэффициенты проницаемости соответственно равны 0,618 и 0,614 мкм2, что соответствует вертикальному направлению. При фильтрации газа под углом 45, 135, 225 и 315° проницаемости образца оказались меньшими, чем для горизонтального направления, но большими, чем для вертикального.
Таким образом, определены проницаемости и доказано, что проницаемость образца изменяется в различных направлениях. Параметр анизотропии исследуемого практически изотропного образца
= kâ/kã = 0,618/0,676 = 0,915.
223

ОПРЕДЕЛЕНИЕ ПАРАМЕТРА АНИЗОТРОПИИ ПЛАСТА ПО КВД
Неоднородность пласта в вертикальном и горизонтальном направлениях характеризуется параметром анизотропии. Он имеет определяющее значение при прогнозировании технологического режима эксплуатации скважин, вскрывших пласты с подошвенной водой или нефтяной оторочкой, при оценке возможности прорыва газа в скважину через перфорированный нефтенасыщенный интервал, при изучении взаимодействия пропластков многопластовых залежей и др. Неоднородность пласта по проницаемости в вертикальном и горизонтальном направлениях изучают в основном экспериментальным путем. В настоящее время практически отсутствуют методы точного определения параметра анизотропии расчетным путем. Оценить значение этого параметра позволяют КВД, снятые в скважинах, вскрывших продуктивный пласт. Для этого, согласно [85], КВД необходимо обработать по формуле
pƒ2 (t) = α − σ t0,5, |
(2.260) |
ãäå |
|
σ = Q0 µz pàò Ò ïë /(πkãÒ ñò 3, 3ƒâ ). |
(2.261) |
Здесь Q0 – дебит скважины перед закрытием; kã – коэффициент горизонтальной проницаемости пласта; kâ = kâpïë/(mµ) – параметр анизотропии (пьезопроводность) в вертикальном направлении.
В формуле (2.261) коэффициент горизонтальной проницаемости находят согласно методике, изложенной в [85].
Чтобы определить коэффициент вертикальной проницаемости kâ, КВД обрабатывают в координатах pƒ2 (t) – 1/t0,5. На полученной графической зависимости выделяют прямолинейный участок и по углу наклона этой прямой опре-
деляют параметр σ.
По известному σ рассчитывают вертикальную пьезопроводность:
â = 0,33[Q0 µ z pàò Tïë/(π kã Tñò σ)]2. |
(2.262) |
При известных pïë и пористости m коэффициент вертикальной проницаемости
kâ = µ m/pïë. |
(2.263) |
Çíàÿ kã è kâ вычисляют параметр анизотропии |
|
ƒ = k"/kã . |
(2.264) |
Порядок обработки КВД для определения параметра анизотропии следующий.
По известным ðç(t) è t рассчитывают pƒ2 (t) , lg t è 1/t0,5. Далее строят зависимость pƒ2 (t) îò lg t. По углу наклона конечного участка этой зависимости определяют значение β. По известному β находят коэффициент горизонтальной проницаемости kã, затем строят зависимость pƒ2 (t) îò 1/t0,5. На графике выделяют прямолинейный участок так, чтобы время t, соответствующее его оконча-
224

нию, было меньше времени, соответствующего началу прямолинейного участка в координатах pƒ2 (t) – lg t. По этому участку определяют уклон σ. По известному σ, используя β и с учетом формулы (2.263), определяют kâ:
k = [hβ |
mµ/(2,09 σp0,5 )]2 = 0,229mµh2 β2 /(p |
Cë |
σ2 ). |
(2.265) |
" |
|
|
|
По известным значениям работающей (вскрытой) толщины hâñê, σ и β, а также используя прямую, построенную в координатах pƒ2 (t) – 1/t0,5, можно вы- числить толщину пласта h:
h = h"“* /[1 − 1,5t β/(2,09 σ)]. |
(2.266) |
По известному kãh/µ, найденному через β, зная значение h, вычисленное по формуле (2.266), если другими способами h не удается определить, рассчи- тывают kã, а затем – по известным kâ è kã – параметр анизотропии. При правильно проведенной обработке отношение hâñê/h не должно превышать 0,4. В противном случае результаты могут быть искажены.
Пр и мер. Рассмотрим задачу определения параметра анизотропии и работающей толщины пласта по КВД, снятой в скважине с исходными данными,
приведенными в табл. 2.36, и при Q0 = 106 ì3/ñóò; hâñê = 6 ì; m = 0,08; Òïë = = 318 Ê; µïë = 0,012 ìÏà ñ; z = 0,84.
Результаты обработки также приведены в табл. 2.36 и показаны на рис. 2.48. По рис. 2.48, à определена величина β = 13 МПа2.
Первая точка прямолинейного участка на рис. 2.48, à соответствует t = = 10 800 ñ. Íà ðèñ. 2.48, á выделен прямолинейный участок с уклоном σ = = 440 МПа2 ñ–0,5. Окончанию этого прямолинейного участка соответствует время t = 3000 с. По формуле (2.266) определена относительная толщина hâñê/h = = 0,226 è h = 26,7 м. С учетом β и h = 2,67 м вычислены kã = 0,0146 ìêì2 è kâ = 0,00407 ìêì2. Следовательно = 0,00407/0,0140 = 0,28.
Рис. 2.48. Результаты обработки КВД в разных координатах
225
Ò à á ë è ö à 2.36
Данные для вычисления параметра анизотропии
t, c |
ðç(t), ÌÏà |
pƒ2 (t), |
lg t |
1/t0,5 |
|
t, c |
ðç(t), ÌÏà |
pƒ2 (t), |
lg t |
1/t0,5 |
|
|
ÌÏà2 |
|
|
|
|
|
ÌÏà2 |
|
|
120 |
22,93 |
525,78 |
2,079 |
0,0913 |
|
6000 |
23,39 |
547,09 |
3,778 |
0,0129 |
180 |
22,98 |
528,08 |
2,255 |
0,0745 |
|
7200 |
23,43 |
546,96 |
3,857 |
0,0118 |
399 |
23,07 |
532,22 |
2,477 |
0,0577 |
|
8400 |
23,46 |
550,37 |
3,924 |
0,0109 |
600 |
23,09 |
533,15 |
2,778 |
0,0408 |
|
9600 |
23,48 |
551,31 |
3,982 |
0,0102 |
900 |
23,16 |
536,39 |
2,954 |
0,0333 |
|
10 800 |
23,50 |
552,25 |
4,033 |
0,00962 |
1200 |
23,21 |
538,70 |
3,079 |
0,0289 |
|
12 000 |
23,52 |
553,19 |
4,079 |
0,00913 |
1800 |
23,25 |
540,56 |
3,255 |
0,0236 |
|
13 200 |
23,53 |
552,66 |
4,120 |
0,0087 |
2400 |
23,28 |
541,95 |
3,379 |
0,0204 |
|
14 400 |
23,53 |
553,66 |
4,158 |
0,0083 |
300 |
23,30 |
542,89 |
3,477 |
0,0183 |
|
18 000 |
23,56 |
555,07 |
4,255 |
0,00745 |
3600 |
23,30 |
544,29 |
3,556 |
0,0167 |
|
86 400 |
23,73 |
563,11 |
4,939 |
0,0034 |
4200 |
23,34 |
544,75 |
3,623 |
0,0154 |
|
172 800 |
23,80 |
566,44 |
5,231 |
0,0024 |
4800 |
23,37 |
546,16 |
3,681 |
0,0144 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РЕШЕНИЕ ОБРАТНЫХ ЗАДАЧ ПО ОПРЕДЕЛЕНИЮ ФИЛЬТРАЦИОННО-ЕМКОСТНЫХ СВОЙСТВ ПЛАСТОВ
Значительное число процессов, связанных с освоением газовых месторождений, можно описать дифференциальными уравнениями. В связи с этим важное значение имеет изыскание методов решения обратных задач. Класс обратных задач довольно широк. Это могут быть инверсные, или коэффициентные обратные задачи (идентификация параметров изучаемого объекта по экспериментальным данным), граничные обратные задачи (определение граничных условий – при известной математической модели и наличии информации о поведении системы, времени – по известным состояниям в более поздние моменты времени или по дополнительно заданной граничной информации).
При решении обратных задач возникают трудности как чисто технические, например методическая организация вычислений, так и носящие принципиальный характер, т.е. могут отсутствовать однозначность, сходимость, возникать неустойчивость к погрешностям входной информации.
Ряд задач газонефтепромысловой механики, таких, как нестационарная фильтрация жидкости и газа в пористой среде, могут быть описаны уравнениями в частных производных параболического типа. Следовательно, исследование таких процессов требует постановки соответствующих граничных и начальных условий, а также знания характеристик исследуемых систем.
1. В случаях когда скважина (галерея скважин) эксплуатировалась длительное время при нестационарных режимах, постановка информации о процессе на границах рассматриваемых систем имеет определенные граничные условия при отсутствии начальных. Задачи подобного типа, например, возникают, когда по результатам измерений забойного давления и дебитов скважин, изменяющихся во времени, необходимо восстановить распределение пластового давления вокруг скважины (галереи скважин) в нефтяном или газоносном пласте. Возникающая при этом задача определения начальных условий из дополнительно заданных условий на границе относится к классу обратных задач и является в общем случае некорректной задачей в смысле устойчивости к малым возмущениям входной информации и требующей построения регуляризующих алгоритмов получения приближенных решений.
Математическая постановка задачи следующая:
226
du = k d2u , t < 0, 0 < x < 1; |
(2.267) |
||||
dt |
dx2 |
|
|
||
u(0, t) = ϕ1(t), |
u(1, t) = ϕ2(t); |
(2.268) |
|||
|
k du |
|
|
= ϕ2 (t). |
(2.269) |
|
|
||||
|
dt |
|
x=0 |
|
|
|
|
|
|||
Необходимо восстановить u(õ, 0). Здесь t – время стабилизации режима. Рассмотрим подход к решению поставленной задачи.
Обозначив неизвестное пока начальное распределение u(x, 0) через v(x), составим формально две задачи: первая – уравнение (2.267), условия (2.268) с начальными условиями v(x); вторая – уравнение (2.267), второе условие из (2.268) с теми же начальными условиями v(x). Тогда за приближение к истинным начальным условиям u(x, 0) берется функция v (x), минимизирующая некоторый функционал от разности двух выше введенных задач, т.е., рассматривая как управление, задачу нахождения можно сформулировать как оптимизационную.
Возьмем в качестве функционала, подлежащего минимизации, функционал
τ(v) = ||u1 – u2||2, |
(2.270) |
ãäå u1 è u2 – решения выше определенных задач.
Известно, что минимизация функционала является в общем случае некорректной задачей, поэтому введем в рассмотрение функционал
τε(v) = τ(v) + ε||v||2, |
(2.271) |
где ε – положительный параметр.
Минимизация этого функционала является уже корректной, и при τε → 0 vε → v. Выбор параметра ε зависит от уровня погрешности входной инфор-
мации.
Следует отметить: в случаях когда известно, что искомое распределение u(õ, 0) является монотонной функцией, задача минимизации функционала (2.270) считается из L2(0, 1).
Численную реализацию такого подхода можно осуществить следующим образом. Производя дискретизацию пространственной и временной координат, задачу минимизации функционалов (2.270) и (2.271) можно рассматривать как задачу векторной оптимизации. Решения u1 è u2 на каждой итерации можно находить тем или иным сеточным методом. С использованием одного из методов нелинейного программирования алгоритм реализован на ЭВМ в виде пакета программ. Проведен ряд тестовых экспериментов. Полученные результаты (рис. 2.49) дали удовлетворительное совпадение с проверочными (истинные и расчетные значения показаны соответственно точками и линией).
2. Часто в процессе разработки и эксплуатации нефтяных, газовых и газоконденсатных месторождений фильтрационные параметры пласта изменяются во времени вследствие отложения парафина, выпадения конденсата, ползучести горных пород и т.д. При изучении таких процессов в уравнении (2.267) коэффициент k является функцией времени. Важный практиче- ский интерес представляет определение этого коэффициента по измеряемым в ходе процесса параметрам. Постановку задачи можно записать в следующем виде:
227

Рис. 2.49. Зависимость функционала τ(v) îò |
Рис. 2.50. Зависимость функции k(t) îò âðå- |
координаты границы |
ìåíè |
du = k(t) d2u ; |
(2.272) |
|||
dt |
dx2 |
|
||
t > 0, 0 < x < 1; |
(2.273) |
|||
u(0, t) = f1(t); |
(2.274) |
|||
u(1, t) = f2(t); |
(2.275) |
|||
k(t) |
du |
(0, t) = f3 (t). |
(2.276) |
|
dt |
||||
|
|
|
||
Условия (2.273), (2.274) и (2.276) можно интерпретировать как значения давления или температуры, измеренные на границах и в начальный момент времени. Тогда принятое условие можно трактовать как измерение расхода или величины теплового потока.
Используя информацию (2.273)–(2.276), определение коэффициента k(t) можно свести к следующей оптимизационной задаче. За приближенное решение принимают функцию k (t), на которой достигается минимум функционала
T |
|
τ(k) = ∫[u1(0, t) − f1(t)]2 dt + ε|k|2, |
(2.277) |
0 |
|
ãäå T – время наблюдения за процессом на границе исследуемой системы; u1 – решение задачи (2.272), (2.274)–(2.276); ε – параметр регуляризации.
Выбор параметра ε обусловлен дисперсией погрешности измерений. Если решение ищется в классе монотонных функций, то минимизация функционала (2.277) является корректной в условиях ε = 0 и u(0, t).
Численную реализацию этой задачи можно осуществить методом, рассмотренным ранее. Апробацию алгоритма проводили на модельных задачах. На рис. 2.50 приведены результаты истинного решения и решения, полученного с помощью использованного алгоритма (показаны соответственно линией и точ- ками).
228

2.11. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ФИЛЬТРАЦИОННОГО СОПРОТИВЛЕНИЯ ПО РЕЗУЛЬТАТАМ ИССЛЕДОВАНИЯ ВЕРТИКАЛЬНЫХ ГАЗОВЫХ СКВАЖИН ПРИ НЕСТАЦИОНАРНЫХ РЕЖИМАХ
Âнастоящее время газогидродинамические методы исследования скважин
èпластов можно применять лишь к условиям однородного пласта и строго радиального притока. Имеется ограниченное число методов, учитывающих простейшие неоднородности [85]. Практически невозможно разработать гидродинамическую модель, учитывающую все макро- и микронеоднородности нефтегазоносного пласта.
Для обработки данных исследования скважин и пластов предлагают применять методы идентификации.
Рассмотрим газовый пласт как объект автоматического регулирования, на вход которого подается некоторый сигнал õ(t), а на выходе регистрируется реакция ó(t). Задачу идентификации можно сформулировать следующим образом: по результатам наблюдений над входными и выходными переменными объекта подобрать оптимальную модель, а по выбранной модели оценить параметры объекта.
Примем в качестве входного воздействия депрессию на пласт õ(t) = ∆ð2(t), а выходной реакцией будем считать дебит: ó(t) = Q(t).
Уравнение, описывающее работу газового пласта, запишем в виде
T |
d∆p2 (t) |
+ ∆p2 |
(t) = aQ (t) + bQ 2 (t), |
(2.278) |
|
||||
|
dt |
|
|
|
ãäå Ò – характерное время переходного процесса в пласте; Q (t) – дебит газа, приведенный к нормальным условиям.
Определим коэффициенты a, b и время Ò из уравнения (2.278). Для этого проинтегрируем (2.278) по t и разделим обе части равенства на ∆ð2(t):
|
Òϕ(t) + 1 = aQ(t) + b Q2(t), |
|
|
|
(2.279) |
||||
ãäå |
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
t |
|
|
|
|
∫∆p2 (t)dt |
|
∫Q(t) dt |
∫Q 2 (t) dt |
|
||||
ϕ(t) = |
0 |
; F (t) = |
0 |
|
; L(t) = |
0 |
|
. |
(2.280) |
∆p2 (t) |
∆p2 |
|
∆p2 |
|
|||||
|
|
(t) |
(t) |
|
|||||
В случае дискретности измерений имеем при i = 1, n
n
ϕ(t) = ∑∆pi2 (t)dt/∆pn2 (t);
i=1
n
F (t) = ∑∆Qi (t) dt /∆pn2 (t); (2.281)
i =1
n
L(t) = ∑∆Qi2 (t) dt/∆pn2 (t).
i =1
229
Ò à á ë è ö à 2.37
Результаты измерения давлений
t, c |
py, ÌÏà |
pç, ÌÏà |
|
t, c |
pó, ÌÏà |
pç, ÌÏà |
5 |
19,5 |
23,5 |
|
50 |
23,8 |
28,5 |
10 |
21,0 |
25,3 |
|
60 |
24,0 |
28,8 |
20 |
22,2 |
26,7 |
|
120 |
24,1 |
28,9 |
30 |
23,0 |
27,6 |
|
180 |
24,2 |
29,0 |
40 |
23,5 |
28,2 |
|
300 |
24,2 |
29,0 |
|
|
|
|
|
|
|
Решив уравнение (2.278) и использовав опытные данные, найдем a, b è Ò. Разделив обе части уравнения (2.279) на L(t), получим
Ò + ϕ(t) |
= a |
F(t) |
+b. |
(2.282) |
L(t) |
|
|||
|
L(t) |
|
||
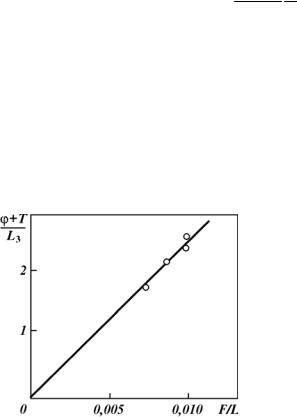
Построив опытные данные в координатах [Ò + ϕ(t)] – L(t) è F(t) – L(t), получим прямую, отсекающую на оси ординат отрезок, равный b; тангенс угла наклона прямой дает искомый коэффициент a.
Согласно приведенной методике обработки кривой восстановления забойного давления, необходимо рассчитать приток газа в скважину после ее закрытия.
Для газовой скважины
q(t) = Ω“*"T“2 dp% , p=2 z“! T“! dt
ãäå Ωñêâ – геометрический объем скважины, м3. Суммарный приток в случае дискретных измерений
V(t) = |
Ω |
T |
p(t) |
− |
p(t = 0) |
||
“*" “2 |
|
|
|
. |
|||
p T |
z(t) |
z(t = 0) |
|||||
|
=2 |
“! |
|
|
|
|
|
Пр и мер. В табл. 2.37 приведены данные о восстановлении давления в скв. 56 месторождения Шатлык. Коэффициенты фильтрационного сопротивления, определенные по индикаторной диаграмме: à = 253 ÌÏà2/(òûñ. ì3/ñóò); b = 0,13 ÌÏà2/(òûñ. ì3/ñóò)2. Вычисленные значения: à = 312 ÌÏà2/(òûñ. ì3/ñóò); b = 0,019 ÌÏà2/(òûñ. ì3/ñóò)2.
На рис. 2.51 представлен график обработки КВД по этой скважине.
Рис. 2.51. Результаты обработки КВД по скв. 56 месторождения Шатлык
230
