2003_МИРЗАДЖАНЗАДЕ А.Хи др.-Основы технологии добычи г / 2

целью ее апробации выделили несколько газоконденсатных скважин Оренбургского месторождения, на которых проводили исследовательские работы. В каче- стве примера на рис. 2.4 приведены кривые 1, 2, 3 восстановления давления (КВД) соответственно по скважинам 168, 107, 18. Характерная особенность – наличие горизонтальных участков (плато) на КВД, которые можно объяснить на основе следующей гидродинамической модели.

Рассмотрим фильтрацию газа в двухпластовой системе со слабопроницаемой глинистой перемычкой. Для радиально-симметричного пласта имеем линеаризованное уравнение

βi

∂p2

=

k

1

∂

∂p2

+(−1)i+1qC,

(2.36)

i

i

r

i

µ

r

∂t

∂r

∂r

ãäå βi, ki – упругоемкость и проницаемость i-го пласта соответственно; qï – плотность перетоков жидкости между пластами.

Для упрощения расчетов остановимся на случае, когда проницаемость одного пласта пренебрежимо мала по сравнению с проницаемостью второго, а упругоемкость второго пренебрежимо мала по сравнению с упругоемкостью первого. Пусть k1 << k2 è ε = β2/β1 << 1, тогда система дифференциальных уравнений (2.36) сведется к виду

p,“. 2.4. j!,"/å "%““2=…%"ëå…, ƒ=K%L…%ã% ä="ëå…, C% “*"=›,…=ì n!å…K3!ã“*%ã% ìå“2%!%›- äå…,

111

		∂ð2	=			1		qC;
		1
		∂t				β
						1
				2					1
		ε1 ∂ð2				=	õ
									r
			∂t
				ð2			− ð2
	qC =
						2	1
							τ

∂ r ∂ð2 − 1 q ; ∂r ∂r2 β1 C

β1,

ãäå x = k2/(β1 µ).

(2.37)

(2.38)

Фильтрация жидкости в двухпластовой системе при сделанных предположениях соответствует случаю, когда основные запасы жидкости сосредоточены во втором пласте, а движение жидкости к скважине происходит по первому. Эти уравнения описывают также фильтрацию жидкости в трещинно-пористых средах.

При решении аналогичных задач обычно предполагают, что переток жидкости между пластами пропорционален перепаду давления между ними, согласно (2.38). Кривая восстановления давления в этом случае сначала резко возрастает до некоторого значения, а затем монотонно приближается к пластовому давлению. Если полностью пренебречь упругоемкостью второго пласта, то в начальный момент времени получим скачок забойного давления с последую-

щим ростом до pCë2 .

Задавая перетоки между пластами в виде (2.38), тем самым предполагаем, что равновесное состояние между перепадом давления в пластах и перетоками достигается мгновенно. В действительности равновесное состояние реализуется с некоторым запаздыванием в силу инерционности системы. Чтобы учесть запаздывание скорости перетоков по сравнению с изменением перепада давления между пластами, заменим выражение (2.38) идентификационным уравнением вида

	∂q	C	+ q		=	p	2	− p	2	β ,
Ò				C			2	1			(2.39)
	∂t							t	1

ãäå Ò – характерное время.

Пусть к моменту времени t = 0 распределение давления в системе было стационарным, соответствующим постоянному дебиту q. В момент времени t = 0 скважина закрывается. Поставленная задача сводится к решению системы уравнений (2.37), (2.39) с граничными и начальными условиями:

π

k h

r

∂p2

= 0;

p

2

= p

2

= p

2

;

2

2

µ

∂r

r=r

1

R=r

2

R=r

Cë

c

(2.40)

p2

= p2

= p2

−

q

µ

ln

R

.

1

t=0

2

t=0

Cë

2π k2h

r

Перетоки жидкости

между

пластами

определяются дифференциальным

уравнением (2.39), причем qC t=0 = 0. Для сведения граничных условий к однородным введем новые функции pi (r, t) − pCë2 (i = 1, 2).

112

Применив преобразования Лапласа по времени, с учетом уравнения (2.39)

для изображения функций

εβ1 Sp)ˆ2 +

p è

p

получим

1

2

)

qµ

R

)

)

pˆ − pˆ

Sp1 +

ln

=

2

1

;

2πk2h

r

t (TS +1)

qµ

R

1 ∂

k

)

)

)

ln

=

r

∂pˆ

pˆ − pˆ

.

(2.41)

2

2

2

1

2πk h

r

r ∂r

µ

∂r

t (TS + 1)

2

$ p1,

Исключим из последней системы дифференциальных уравнений функцию тогда

ˆ

qµ

R

1 ∂

k

$ˆ

$ˆ

+ [qµ /(2πk h)] ln(R / r)

+

ln

=

r

∂p

−

Sp

.

(2.42)

ε Sp2

2

2

2

2

$

2

πk h

r

β r ∂r µ

∂r

tS (TS + 1) + 1

2

1

Решение (2.42) будем искать в виде ряда по собственным функциям оператора Штурма – Лиувилля:

L

= −

1

d

r

k2

dp

;

p

= 0; pr =R = 0.

(2.43)

p

µ

r=r

r dr

dr

c

Можно показать, что разложение функции ln(R/r) по собственным функциям оператора имеет вид

µ			∞	pi(rc)
	ln	R	= ∑		pi(r),	(2.44)
k		r		λ
2			i=1	i

ãäå ði(r) – нормированные собственные функции; λi – собственные числа. Подставив выражения (2.43), (2.44) в уравнение (2.42), получим

∞

ε SC +

q

pi(rc)

+ λiCi +

SCi

+ [q /(2πh)][pi(rc) / λi]

∑

p

(r ) = 0.

(2.45)

i

2πh

λ

β

tS (TS +1) +1

i

c

i

i

i=1

Из последнего

соотношения

найдем коэффициенты

разложения

ôóíê-

$

öèè p2:

Ci = −

q pi(rc)

ε[tS(TS + 1) + 1] +1

.

(2.46)

2πh

λ

i

(εS + λ

/β )[τS(TS +1) +1] + 1

i

1

Тогда

(rc,S) =

p2

−

q

∞

U2

ε[tS(TS + 1) + 1] + 1

(2.47)

p2

S

2πh

∑ λ

(εS + λ /β )[τS(TS +1) +1] + 1;

$

Cë

1

i=1

i

i 1

U2

= p2

(r ).

1

1

c

Для выявления особенностей КВД при наличии неравновесных перетоков остановимся на частном случае, когда λit/β1 >> 1. Тогда из уравнения (2.47)

l

2

∞

2

ε

∞

2

ε

=

ðïë

−

q

∑

Ui

+∑

Ui

p2

.

(2.48)

S

2πh

λ

i

εS + λ

i

/ β

λ

i

(εS + λ / β )Tt[S2 + S / T +1 /(Tt)]

1

i =1

i 1

i =1

113

В зависимости от соотношения между характерными временами стационарных и неравновесных перетоков t è Ò получим следующие выражения для КВД:

ïðè t > 4Ò

2

q

∞ U2

−λ

t /β

1

−α t

−α

t

ð2

= ðCë −

∑

i

À1å

i

2

+

(A2e

1

− A3e

2

)

;

(2.49)

2πh

i=1

λi

εTt

ïðè t = 4Ò

2

q

∞

U2

−λ

t /β

1

−t /(2T)

ð2 =

ðCë −

∑

i

B1å

i

2 +

(B2

− B3)e

;

(2.50)

πh

εTt

2

i=1

λi

ïðè t < 4Ò

2

q

∞

U 2

−λ

t

/

β

1

−t /(2T )

ð2 =

ðïë

−

∑

i

C1å

i

2

+

(C2 sin Ωt + C3 cos Ωt)e

;

(2.51)

λi

2πh

i =1

εTt

ãäå

1

i

1 τ

α =

+(−1)

−1 ;

(2.52)

i

2T

Òt 4Ò

Ω =

1

τ

−1 ;

(2.53)

Òt 4Ò

Ài, Bi, Ci – дробно-рациональные функции относительно переменных 1/(2Ò), λi/β2, [1/(Tt)][t/(4T) −1]. Явный вид этих коэффициентов здесь не приво-

дится в связи с громоздкостью выражений.

Анализ уравнений (2.49), (2.50) показывает, что при t ≥ 4Ò и малых временах происходит интенсивный рост давления, затем его уменьшение до некоторого значения с последующим ростом до пластового. При этом с уменьшением эффекта неравновесности, т.е. при Ò → 0, интервал немонотонности КВД также уменьшается, и в предельном случае Ò = 0 (равновесный переток) давление монотонно возрастает до ðïë, что можно объяснить следующим образом. При запаздывании перетоков по сравнению с изменением перепада давления между пластами в начальный момент времени в высокопроницаемом пропластке происходит восстановление давления, как в изолированном пласте. Возникающий

при этом перепад p22 – p21 вызывает затем возрастающий отток жидкости из

высокопроницаемого пропластка, вследствие чего давление в нем начинает падать, а в слабопроницаемом возрастать. По мере выравнивания давлений интенсивность перетоков уменьшается до нуля, и давление в системе вновь возрастает до ðïë. В случае когда t < 4Ò, т.е. когда неравномерность превалирует над характерным временем перетоков, в системе могут возникнуть затухающие автоколебательные процессы.

114

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СОВМЕСТНО РАБОТАЮЩИХ ПЛАСТОВ МЕТОДОМ ДЕТЕРМИНИРОВАННЫХ МОМЕНТОВ

В процессе разработки нефтяных, газовых и газоконденсатных месторождений часто осуществляют совместную эксплуатацию нескольких пластов одной скважиной.

При гидродинамических исследованиях скважин, эксплуатирующих несколько пластов, используют скважинные расходомеры. Измеряя приток газа из каждого пропластка, можно определить работающую толщину в исследуемой скважине. Однако не всегда имеется возможность спустить расходомер в забой, иногда этому препятствует конструкция скважины.

Газогидродинамические исследования скважин позволяют получать необходимую информацию о состоянии скважины и продуктивного пласта. Наиболее полное представление о параметрах пласта в процессе его дренирования можно получить при исследованиях на нестационарных режимах, основанных на обработке кривых изменения давления. Однако следует отметить, что на кривую восстановления давления (КВД), снятую при промысловых исследованиях, влияет множество факторов, и она содержит в себе случайные ошибки (помехи). Для получения достоверных сведений о параметрах пласта необходимо осуществлять учет этих случайных помех с помощью вероятностностатистических методов обработки данных исследования скважин и пластов, имеющих повышенную помехоустойчивость.

Одним из таких методов обработки КВД является метод детерминированных моментов, обладающий высокой помехоустойчивостью и позволяющий идентифицировать сложные модели пластов.

Детерминированным моментом k-го порядка функции f(t) называют вели-

÷èíó

∞
αk = ∫tk f(t)dt.	(2.54)
0

Если значение функции f(t) известно в дискретные моменты времени ti, равностоящие с шагом ∆t, òî k-й момент αk вычисляют по формуле

∞
αk = ∫tki f(ti)dt.	(2.55)
0

При снятии КВД определяют изменения ð(t) – забойного давления, отсчи- тываемого от установившегося значения, и Q(t) – затухающего дебита скважины.

Методика определения параметров однородного пласта при условии линейного радиального притока газа к скважине заключается в следующем.

Вычисляют моменты:

α′	=	∞	[ð2	− ð2 (t)]dt;	α′	=	∞ t[ð2		− ð2	(t)]dt;
0		∫	Cë		1		∫	Cë
		0					0
			β′0	∞	β1′		∞
				= ∫Q(t)dt;		= ∫ tQ(t)dt.				(2.56)
				0			0

При исследовании газовых скважин параметры пласта в случае линейного закона фильтрации (без учета реальных свойств газа) определяют по формуле

115

	kh		=1,6				α′Q	− β′∆p2	− 8β′ (α′				− β′ ∆p2			/ Q		0	)			pàò;		(2.57)
							1	1			0	0		0
µ								π(α′	− β′ ∆p2 / Q					0	)2
								0			0
R2			=	16		α′Q		− β′∆p2	− 8β′			(α′	− β′ ∆p2				/ Q			)		p	,	(2.58)
						1 0		1			0	0			0			0
	x			2, 5				α′Q		0	− β′ ∆p2											àò
									0			0

ãäå Q0 – дебит скважины до остановки, приведенный к стандартным условиям; ∆ð2 – установившаяся разность квадратов пластового и забойного давлений.

П р и м е р. В табл. 2.4 приведена КВД в скв. 2 месторождения Северный Балкун. Установившийся дебит скважины составляет 782,5 тыс. м3/сут, установившаяся разность квадратов забойного и пластового давления равна 344,43 МПа2.

Обработку КВД проводили в предположении мгновенного притока к

скважине после ее остановки, поэтому моменты β′

è

β′

функции Q(t) â âûðà-

0

1

жении (2.57) равны нулю. Положив β′

=

β′

= 0, можно определить параметры

0

1

пласта:

kh = 1,6Q0α1′ pàò ;

R2

= 16α1′ .

µ

π(α′0 )2

x

25α′0

Расчеты по формулам (2.57) дали: α′0 = 107 ÌÏà; α1′ =18 1010 ÌÏà2, ñëå-

довательно, kh/µ = 82,98 10–10 ì3/(ÌÏà ñ), R2/x = 125 103 c. Аналогичные расче- ты были проведены и по другим скважинам месторождений Шатлык, Наип и Ачак (табл. 2.5).

Рассмотрим методику, позволяющую определять работающую толщину двух газоносных пластов, эксплуатируемых одной скважиной, по КВД и их суммарному дебиту до остановки скважины. При этом предположим, что приведенные контурные давления в обоих пластах равны. Для решения поставленной задачи применим метод детерминированных моментов.

Обозначим: ði(r, t) – давление газа в i-м пласте (i = 1, 2) в точке r в момент времени t; ðê – давление на контуре питания; ki, hi, mi – соответственно проницаемость, толщина и пористость i-го пропластка; µ – вязкость газа; rñ – радиус скважины; R – радиус контура питания; ð0 – атмосферное давление; ρ0 – плотность в атмосферных условиях; q1 – дебит i-го пласта до закрытия

Ò à á ë è ö à 2.4

Параметры кривой восстановления давления

Время, с	ðç, ÌÏà	p2, ÌÏà2		Время, с	ðç, ÌÏà	p2, ÌÏà2		Время, с	ðç, ÌÏà	p2, ÌÏà2
		ç				ç				ç
0	25,4	645,36		330	30,0	901,02		1800	30,4	924,59
30	25,4	647,14		360	30,1	908,11		2700	30,3	923,87
60	25,6	653,98		390	30,2	913,73		3600	30,3	923,87
90	25,8	655,53		420	30,3	917,48		5400	30,3	923,12
120	27,2	743,59		480	30,3	922,38		7200	30,3	922,38
150	27,5	758,17		540	30,3	923,87		9000	30,3	922,38
180	27,8	773,23		600	30,4	924,59		12600	30,3	922,38
210	27,9	783,38		720	30,4	924,59		16200	30,3	922,38
240	28,2	797,55		900	30,4	925,32		27600	30,4	926,16
270	29,6	823,51		1200	30,4	925,32		70200	31,4	989,79
300	29,8	893,89

116

Š = K ë , ö = 2.5

pеƒ3ль2=2/ %C!еделе…, C=!=ме2!%" -,ль2!=ц,,

	Номер	Расчет по стандартной			Расчет по предлагаемому
Месторождение			методике			методу
	скважины
		À		Â	À		Â
Восточный Шатлык	303	964		0,0043	1006,4		0,0053
	236	2027		0,01	1995,0		0,0093
	102	4293		0,0032	4350,0		0,0070
	25	1560		0,006	1515,1		0,0055
	38	1020		0,0075	1200,1		0,0088
	30	1965		0,0023	1901,3		0,0044
	22	2620		0,0027	2805,0		0,0047
	29	3321		0,0045	3410,0		0,0071
	31	3492		0,0073	3800,0		0,0204
	28	2315		0,002	2390,0		0,0046
	23	626		0,002	815,0		0,0061
À÷àê	503	141		0,006	188,3		0,0030
Северный Наип	11	253		0,0000052	247,6		0,000007
Северный Балкун	38	53		0,00018	136,24		0,0005
	2	60		0,000006	82,98		0,00008

Примечание. À = kh/µ, ìêì2 ñì/(ìÏà ñ);  = x/R3, ñ–1.

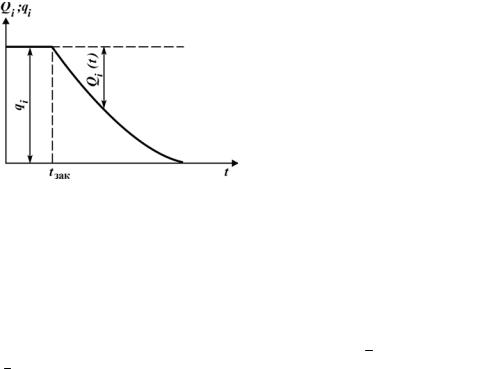
скважины; Qi(t) – изменение дебита i-го пласта после закрытия скважины. Согласно графику изменения qi è Qi от времени (рис. 2.5), Qi(0) = 0, Qi (t)|t→∞ = qi.

Для упрощения последующих выкладок предположим, что дебит каждого пласта известен. В дальнейшем это предположение будет исключено, и при окончательных расчетах используем информацию только о суммарном дебите обоих пропластков. Поскольку определение работающей толщины скважины относится к задачам идентификации, для ее решения требуются дополнительные граничные условия.

Рассмотрим нестационарную фильтрацию газа из кругового пласта. Уравнение движения газа к скважине имеет вид

∂ð2	=	k p		∂2ð2	+	1 ∂ð2
i		i i		1			1	.	(2.59)
∂t		miµi		∂r2		r ∂r

Исследуем процесс восстановления давления в пласте. В этом случае на- чальные и граничные условия задаются следующим образом:

ði(r, 0) = p*2 −

µp=2 qi

ln

r*

;

πk h

ρ

“2

r

i

i

c

∂ði2

(r

,

t) = p2 −

µðàòqi

[q

−Q

(t)];

p

(r

, t) = p2.

∂r

c

ê

πk h

ρ

r

i

i

2

*

*

i i

ñò c

Дополнительное условие:

ði(rc, t)

= p*2 −

µð=2qi

ln

r*

+ f 2(t),

r

πk h

ρ

i i “2

c

ãäå f(t) – известная функция времени, причем такая, что f(0) = 0,

	f 2(t)			= p*2 −	µð=2qi	ln	r*	.
					πk h ρ
			t→∞				r
					i i “2		c

(2.60)

(2.61)

(2.62)

(2.63)

117

p,“. 2.5. j!,"= ,ƒìå…å…, äåK,2= C%“ëå	p,“. 2.6. g=",“,ì%“2ü ∆p2 %2 t
ƒ=*!/2, “*"=›,…/ (tƒ=* $ ì%ìå…2 ƒ=*!/2,
“*"=›,…/)

Уравнение (2.59) – нелинейное относительно зависимой переменной. Приближенные методы – практически единственное средство его эффективного аналитического исследования. Самую широкую область применения имеет метод Л.С. Лейбензона. Он заключается в том, что вместо нелинейного уравнения

(2.59) рассматривают линеаризованное уравнение относительно pi2, причем ве-

личину kipi/(miµ) принимают постоянной. Очевидно, при таком подходе ð(x, t) должно заменяться некоторым характерным давлением p = const, например

p = ðê. Таким образом, предположим, что фильтрация газа описывается линейным по ð2 уравнением

∂ð2		∂2ð2		1 ∂ð2
i	= õi	i	+		∂r		,	(2.64)
∂t		∂r2		r

ãäå xi = kipê / (µmi).

Проведя замену зависимой переменной

ð

(r

, t) = p2(r,t)

− p

2

+

µð=2qi

ln

r*

,

(2.64)

πk h ρ

i

c

*

“2

r

i i

c

получим

∂ð

=

∂2ð2

+

1

∂ð

;

(2.66)

∂t

õi

i

∂r2

r

∂r

pi(r, 0) = 0;

(2.67)

∂ði (r ,

t)

= −

µðàò

Q

i

(t);

(2.68)

∂t

c

πkihirc

pi(r, t) = 0;

(2.69)

p2

(r

,t)

= f 2 (t) = ∆p2 − ∆p2 (t) = ∆p2 (t);

∆p2

= const.

(2.70)

1

c

0

›

0

На рис. 2.6 приведена зависимость ∆ð2(t) и показана величина ∆p02 – разность квадратов давления перед закрытием.

Точка À1 соответствует разности p*2 – [µpàòqi/(πkihiρ0)]ln(rê/rc).

118

Решение (2.66)–(2.69), связывающее ∆ð2(t) ñ Q(t), в преобразованиях Лапласа имеет вид

l

πki hi ρ0 rc

S 0

(

) 1 (

)

1 (

)

0

(

)

l

Qi(S) = −

k

a

I

b

+ k

b

I

a

∆p(S),

(2.71)

µp0

(a)I0 (b)

− k0 (b)I0

x k0

(a)

ãäå

à =

S

R;

b =

S

r .

xi

xi

c

Разложим выражение в фигурных скобках в ряд по степени S. Известно,

÷òî

k (z) = − ln

kz

+

z2

1− ln

kz

+

z4

3

− ln

kz

+... ;

0

2

2

4

2

4 16

2

k (z) =

1

+

z

ln

kz

−

1

+

z3

ln

kz

−

5

+

z

2

ln

kz

−

5

+...;

(2.72)

1

z

16

2

6

2

2 2

2

4

64

3

I0(z)

=1 +

z2

+

z4

+

z6

+...;

4

16

36 64

4

I1(z) = 2z + 16z3 + 6 z564 +... ,

ãäå k – некоторая постоянная величина.

Используя выражение (2.72) и пренебрегая членами, содержащими rc по сравнению с членами, содержащими R, получаем

R2

R4

1

R6

1 +

S +

S

2

+

S

3

Qi(S) =

πk h ρ

0

4xi

16x2

36

16x3

×

l

i i

i

i

µp0

R2

1

R

4

3

2

R4

3

3

1

+

1 −

S +

1 −

S

+

1 −

S

R

R

R

4xi

ln

64xi2

2 ln

36

64xi3

6 ln

r

r

r

c

c

c

$ˆ2

(S)

×

∆p

.

(2.73)

ln

R

rc

Разложив знаменатель выражения (2.73) в ряд по S и умножив на числитель, имеем

l	πkihiρ0
Qi(S) =							1	+
					R
	µp	0		ln
					r
					c
	+				R4
			64xi3 ln3 R
							rc

R2

S +

R4

1

−

5

ln

R

S2 +

R

2

2

R

r

8

4xi ln

rc

16xi ln

rc

c

1 −

5

ln

R

+

23

ln2

R

S3

∆p(S).

(2.74)

4

rc

54

rc

119

Обозначим

πk h ρ

0

= ai;

πk h ρ

0

R2

i

i

i

i

µp

0

ln(R/r )

µp

ln(R/r )4x

i

ln(R/r )

c

0

c

c

µp

πk h ρ

R4

1−

5

R

=

ln(R/r ) 16x2

ln2(R/r )

8 ln r

i

i 0

0

c

i

c

c

πk h

ρ

0

R4

1

−

5

ln

R

+

23

ln2

i

i

µp

ln(R/r )

64x

3

ln3(R/r )

4

r

54

0

c

i

c

c

= bi;

ci;

(2.75)

R = di. rc

С учетом обозначений (2.75) формула (2.74) примет вид

l	2	+ di S	3	l	(2.76)
Q i (S) = {ài + biS + ciS				+ ...}∆p(S).

При совместной работе двух пластов, эксплуатируемых одной скважиной, дебит равен сумме дебитов каждого пропластка, т.е.

l

(S) + Q2(S) = {∑ ài + S∑ bi

+ S

2

∑ ci +

S

3

2

(S) =

Q i (S) = Q1

∑ di + ...}∆p

{

}

$2

= à + bS + cS

2

+ dS

3

+

(S).

(2.77)

... ∆p

Рассмотрим функции Q(t) è ∆ð(t). Преобразование Лапласа от ∆ð2(t) можно разложить в ряд по степеням S:

∆ð

2 (t) = ∆p2

− ∆p2

(t);

0

$ˆ2

∆p02

∞

S2t2

S3t

3

2

∆p

(S) =

−

∫

1

− St +

−

+... ∆p

(t)dt =

S

2

6

0

2

∞

∞

S2

∞

=

∆p0

− ∫

∆p2 (t)dt + S∫ t∆p2 (t)dt −

∫ t2 ∆p2

(t)dt +... =

S

0

0

2

0

=

∆p02

− α

0

+ α

1

S − α

2

S2

+... .

(2.78)

S

2

Поскольку приток газа после остановки скважины незначителен, будем

считать, что Q(t) = f(tq) = f [t(q1+q2)]. Следовательно,

l

(2.79)

Q(S) = q/S.

Подставив выражение (2.78), (2.79) в уравнение (2.77) и перемножив полиномы, получим

q	= a	∆p02	− (α	a − ∆p b) + (α		a − α	b + ∆p2c)S −
S		S	0	0	1	0	0

−(α	a − α b + 2	α	c − 2∆p2	α)	S2	+... .	(2.80)
2	1	0	0	2

Для определения à, b, c è d приравняем в выражении (2.80) члены справа и слева при одинаковых степенях S:

q = a∆p02; 0 = α0a − ∆p02b;

120