1 Общая теория уравнивания по методу наименьших квадратов

Суть метода наименьших квадратов заключается в следующем. Даны результаты измерений некоторых величин у_i(i = 1, 2,…,n). Эти величины являются функциями других величин x_j(j=1,2,...,k), число которых k<n. Ставится задача: найти оптимальные оценки величин x_j по результатам измерений величин у_i. Результаты измерений, следуя проф. А. С. Чеботареву [9], обозначим через q_i. Таким образом, можно написать n уравнений

y_i=f_i(x₁,x₂,…,x_k)=q_i+Δ_i (i=1,2,…,n)

где _i -истинные ошибки результатов измерений.

Истинные ошибки в большинстве случаев узнать невозможно. Поэтому в равенствах (1.1) их наменяют поправками v_i. Если задача определения оптимальных оценок для x_i решается так, чтобы сумма квадратов поправок [v²] была минимальной, то полученный результат называется решением по методу наименьших квадратов, а полученные оценки для x_i - оценками метода наименьших квадратов. Вместо (1.1) напишем теперь

f_i(x₁,x₂,…,x_k)=q_i+v_i (i=1,2,…,n)

Уравнения (1.2) называются начальными уравнениями ошибок. Если измерения неравноточные, то вместо требования

Ф=[v²]=min,

как это будет видно в разд. 4, получим

Ф=[pv²]=min,

где p_i – веса результатов измерений.

Начальные уравнения приводятся к рабочему виду путем их линеаризации. Для этого левую часть уравнений (1.2) разлагаем в ряд Тейлора, удерживая только первые члены разложения:

Начальные значении х₁°, х₂°,...,х_k° могут быть найдены различными путями; например, если это координаты, путем снятия координат с карты. Самый общий путь это решить k уравнений из системы (1.2), считая v_i = 0.

Вид функций в левой части (1.2) должен быть известен. Поэтому в (1.5) известными величинами являются значения функций для начальных значений аргументов f_i(х₁°, х₂°,...,х_k°), значения производных для начальных значений аргументов и результаты измерений q_i(i=1,2, ...,n). Известные слагаемые этих уравнений объединяем в так называемые свободные члены:

Коэффициенты при неизвестных поправках x_i обозначим следующим образом: коэффициенты при x₁ при помощи буквы a:

при x₂ при помощи буквы b:

и так далее, а при x_k при помощи g:

В результате получаем рабочую форму уравнении поправок, которые также иногда называются уравнениями ошибок, уравнениями погрешностей, а в астрономии также условными уравнениями, что в геодезии недопустимо, так как в геодезии под условными уравнениями понимается нечто другое. Наиболее правильное названии - это «уравнения поправок», потому что эти уравнения связывают поправки в искомые неизвестные с поправками в результате наблюдений:

Для определения поправок x_j используем условие (1.4), т. е. находим частные производные и приравниваем их к нулю:

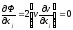
Число полученных уравнений (1.11) равно числу неизвестных. Эти уравнения называются нормальными. Решая систему нормальных уравнений, получают поправки x_j, а следовательно, нужные нам оценки параметров x_j.

Однако форма (1.11) нормальных уравнении не являете рабочей, так как в таком виде в них величины x_j не участвуют. Для получения рабочей формы уравнений найдем сначала . Используя (1.7), (1.8), (1.9), получим

Подставляя (1.12) в (1.11), найдем теперь

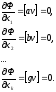
Получили еще одну форму для нормальных, уравнений. Наконец подставив (1.10) и (1.13), получим рабочую форму нормальных уравнения. Без потери общности распишем ее для случая трех неизвестных:

Решая систему (1.11) относительно x_j (j=1,2,…,k), найдем эти неизвестные и уравненные значения параметров