5 Измеряемые функции в триангуляции второго класса

Чтобы применить изложенную теорию к какой-либо практической задаче, нужно уяснить, какие величины в данной задаче являются искомыми неизвестными (параметрами) и какие величины - измеренными функциями. При уравнивании триангуляции второго класса искомыми параметрами являются координаты пунктов триангуляции, измеренными функциями - горизонтальные направления, отнаблюденные на пунктах триангуляции. Принято триангуляцию и горою класса уравнивать на плоскости и проекции Гаусса – Крюгера. Это наиболее просто и достаточно точно. Будем считать в дальнейшем, что результаты измерений спроектированы на плоскость.

Следующим этапом при уравнивании параметрическим способом является определение вида функций, которые связывают измеренные величины с определяемыми. При уравнивании триангуляции второго класса, следовательно, надо найти вид зависимости горизонтальных направлений от координат пунктов триангуляции. С этой целью рассмотрим рис. 1. Обозначим направление с пункта i на пункт j буквой R_ij, координаты пункта j - через x_i, y_i, пункта j – через x_j, y_j.

Рис.1. Определение формы зависимости

Направления от координат

Через z_i обозначен ориентирующий угол - это тот угол, который ориентирует всю систему направлений на пункте i, он равен углу между осью х и начальным направлением на пункте i и отсчитывается от оси х по ходу часовой стрелки. Из рис.1 находим, что тангенс дирекционного угла а_ij направления R_ij равен

,

где

.

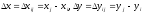Но из рис.1 следует

.

Поэтому окончательно

.

Мы видим, что в выражение для функции, связывающее горизонтальное направление с неизвестными координатами, вошло дополнительное неизвестное – ориентирующий угол.

6 Формулы для коэффициентов уравнений поправок

Согласно общей теории уравнивания коэффициенты уравнений поправок суть производные измеренных функций по искомым параметрам, вычисленные для приближенные значений параметров. Найдем эти производные, используя при этом формулы

Итак,

Уравнение поправок для направления с пункта I на пункт j примет вид

где v_ij - поправка в измеренное направление, а индекс «0» по-прежнему означает, что соответствующие величины взяты для начальных (приближенных) значений аргументов; 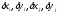- поправки в координаты пунктовi и j. В (6.9) длины сторон удобно выражать в километрах, поправки в координаты - в дециметрах, поправки v_ij в направления - в секундах. Чтобы при этом не нарушить равенство (6.9), необходимо: 1) коэффициенты при поправках в координаты умножить на радиан, выраженный в секундах, т. е. на р" = 206 265"; 2) длины сторон, выраженные в километрах, умножить на 10 000, так как 1км = 10 000 дм. Тогда уравнение (6.9) преобразуется в такое:

где выражено в километрах, а поправки в координаты пунктовi и j получаются выраженными в дециметрах; верхний индекс «ноль» для дирекционных углов и длин сторон означает, что эти величины соответствуют приближенным координатам.

Как показывает выражение (6.10), в этом уравнении поправок коэффициенты при поправках в координаты пункта i отличаются от коэффициентов при поправках в координаты пункта j только знаком. Поэтому для этих коэффициентов приняты такие обозначения:

В (6.11) поставлен знак «минус». Это сделано для того, чтобы члены с поправками в координаты пункта i вычитались из членов с поправками в координаты пункта j по аналогии с формулами (5.2). Таким образом, имеем окончательно

Таких уравнений в сети столько, сколько отнаблюдено горизонтальных направлений. Если пункт i или пункт j «твердый» (устаревший, но удобный термин), т. е. координаты его считаются известными и безошибочными, та в уравнении (6 13) поправки в эти координаты приравниваются нулю и соответствующие члены с этими поправками из уравнения поправок исчезают.