2 Матричная форма получения уравнений поправок

Изложим получение нормальных уравнений в матричной форме. Условимся при этом матрицы обозначать прописными буквами латинского алфавита (за некоторыми исключениями, которые будут оговариваться), векторы малыми буквами латинского алфавита с чертой наверху, элементы матриц и векторов - строчными буквами, в большинстве случаев совпадающими с буквенными обозначениями матриц и векторов. Так, например, введем векторы поправок неизвестных параметров и истинных ошибок:

Функцию у=у(х₁, х₂, ..., x_k) будем рассматривать как функцию векторного аргумента

т.е. у = f(). При этом k функций у_i = f_i (), (i = 1,2, ..., n), образуют вектор-функцию

.

В целях экономии места векторы, под которыми понимается векторы-столбцы, часто будем описывать в виде

где T – знак транспонирования.

В результате система уравнении (1.1) в матричной форме изобразится следующим образом:

Иногда бывает необходимо указывать размерность векторов и матриц. Тогда (2.5) примет вид

где - (₁,₂,...,_n)^T . При замене истинных ошибок поправками получим

где = (v₁,v₂,…,v_n)^T. Система (2.7) - это система начальных уравнений поправок.

Введем вектор приближенных значений неизвестных величин ⁰ = (x₁⁰,x₂⁰,…,x_k⁰)^T. Используем снова разложение в ряд Тейлора, чтобы измеряемые функции представить в линейной форме. При этом ограничимся первыми членами разложения. Получим

.

В этом равенстве - матрица, столбцами которой являются векторы

Индекс «0» в (2.8) означает, что элементы матрицы вычислены для начальных значений аргументов. Таким образом, производная вектора по вектору предстает в виде матрицы, в данном случае обозначим ее через G:

Через х обозначен вектор = (x₁, x₂,,..., x_k )^T. Обозначим через вектор свободных членов:

В итоге получим матричное выражение уравнений поправок в рабочей форме:

Вспомнив обозначения (1.7). (18). (1.9), распишем матрицу G в явном виде

3 Матричная форма получения нормальных уравнений

В этом разделе мы рассмотрим, как получается система нормальных уравнений, исходя из принципа наименьших квадратов в матричной форме. Исходной системой является система уравнений поправок (2.12).

Принцип наименьших квадратов в матричной форме запишется при равноточных независимых измерениях в виде

Поэтому, подставив (2.12) в (3.1), получим

или

Дифференцируем последнее выражение:

Слагаемые в правой части (3.4) являются векторами; чтобы сложить векторы, необходимо их представить в каком-либо одном виде: либо в виде векторов-столбцов, либо в виде векторов-строк, т.е. в транспонированном виде. Учитывая это замечание, (3.4) можно представить в виде

.

Из (3.5) следует

где

- матрица нормальных уравнений, а

- вектор свободных членов нормальных уравнений.

4 Решение задачи уравнивания при неравноточных измерениях

Если измерения неравноточные, то каждому измерению приписывается его вес - степень доверия к этому результату. Вес относительная величина, так как возникает в результате сравнения по точности одних измерений с другими. Но если совместно уравниваются однородные измерения, вес получает размерность. Чем больше дисперсия данной случайной величины, представляющей результаты измерений, тем меньше ее вес, и наоборот, чем меньше ее дисперсия, тем больше ее вес, т.е. вес измерения обратно пропорционален его дисперсии:

,

где к - коэффициент пропорциональности, σ² - дисперсия рассматриваемого измерения, вес которого равен р. Определим коэффициент k. Пусть имеется такое измерение, вес которого р=1. Тогда из(4.1) следует

,

где σ₀² - дисперсия такого измерения, вес которого равен единице. В данном ряду измерении его может и не быть, по всегда можно представить существование такого измерения, дисперсия которого σ₀². Теперь для веса измерений таким образом имеем формулу

.

Далее, пусть, как и в разделе 1, имеем n измеренных функций с k определяемыми параметрами. Однако теперь мы считаем, что измерения неравноточные и каждому измерению q_i соответствует его вес р_i. Пусть результат х имеет дисперсию σ² и вес р. Образуем величину

.

Найдем дисперсию σ_y и вес p_y величины y. Из (4.4) следует

.

По определению

.

Из (4.3) следует

.

Подставляя (4.5) и (4.7) в (4.6), получим

.

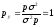Получили важный результат (так называемую лемму Гаусса): Чтобы перейти от неравноточных измерений к равноточным достаточно неравноточные измерении помножить на корень квадратный из соответствующего веса.

Таким образом, достаточно уравнения поправок помножить на корни квадратные из соответствующих весов и решать далее задачу как для равноточных измерений.

Рассмотрим задачу уравнивания при неравноточных измерении и общем виде. В этом случае принцип наименьших

преобразуется следующим образом. Приведем поправки v_i к равноточным: v_i’ = v_i , где v_i’ - поправки, соответствующие равноточным измерениям. Согласно (4.9) имеем

.

В матричной форме

,

где Р – матрица весов, имеющая при независимых измерениях диагональный вид

.

Уравнения поправок имеют тот же самый вид, что и при равноточных измерениях. Дифференцируя (4.11) и приравнивая нулю производные, будем иметь

В результате получили нормальные уравнения в сокращенной форме:

Подставим в (4.14) выражения для v из (1.10), получим нормальные уравнения в рабочем виде. Не теряя общности, распишем эту систему для случая трех неизвестных:

Так как и в матричной форме минимизируемая функция Ф имеет вид (4.11), то производная

.

Но

.

Следовательно, приравнивая нулю , получим

Обозначим

Легко проверить, что А – это матрица системы нормальных уравнений (4.15), а l₁ – столбец свободных членов этой системы. Таким образом, получили систему нормальных уравнений: