
- •Кандидат физико-математических наук, доцент кафедры математики бгита н.А. Часова
- •Понятие функции нескольких переменных
- •Предел функции. Непрерывность
- •Частные производные и дифференцируемость функции. Дифференциал
- •Производная по направлению. Градиент
- •Производная сложной функции
- •Частные производные и дифференциалы высших порядков
- •Неявные функции
- •Касательная плоскость и нормаль к поверхности
- •Экстремумы функции двух переменных
- •Задачи о наибольших и наименьших значениях
- •Примеры решения задач
- •Задания для самостоятельного решения
- •Интегральное исчисление функций нескольких переменных
- •Контрольная работа по теме
- •«Двойной интеграл и его приложения»
- •Теоретическая часть
- •1. Определение двойного интеграла
- •Геометрический смысл двойного интеграла
- •2. Некоторые свойства двойного интеграла
- •3. Вычисление двойного интеграла повторным интегрированием
- •4. Замена переменных в двойном интеграле
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Контрольная работа по теме «Криволинейные интегралы» Теоретическая часть
- •1. Определение криволинейного интеграла второго рода
- •2. Некоторые свойства криволинейного интеграла второго рода
- •3. Существование и вычисление криволинейных интегралов второго рода
- •4. Формула Грина-Остроградского
- •5. Криволинейные интегралы, не зависящие от пути интегрирования
- •Нахождение функции по ее полному дифференциалу
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Ответы Дифференциальное исчисление функций нескольких переменных
- •Двойной интеграл и его приложения
- •Криволинейные интегралы
- •Литература
Задачи для самостоятельной работы
Задача 1. Найти интеграл.
1.1.
 ,
,
![]() .
.
1.2.
 ,
, ![]()
1.3.
 ,
, ![]() .
.
1.4.
 ,
,
![]() .
.
1.5.
 ,
, ![]()
1.6.
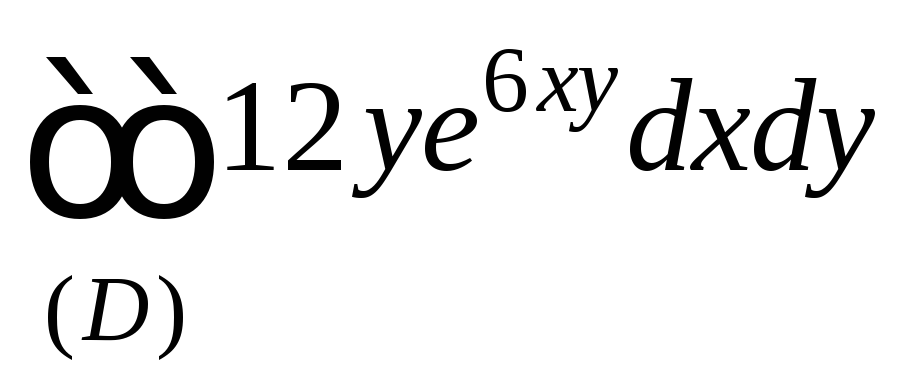 ,
,
![]() .
.
1.7.
 ,
, ![]() .
.
1.8.
 ,
, ![]() .
.
1.9.
 ,
, ![]()
1.10.
 ,
, ![]() .
.
Задача 2. Найти интеграл.
2.1.
 ,
,
![]() .
.
2.2.
 ,
,
![]() .
.
2.3.
 ,
,
![]() .
.
2.4.
 ,
,
![]() .
.
2.5.
 ,
,
![]() .
.
2.6.
 ,
,
![]() .
.
2.7.
 ,
,
![]() .
.
2.8.
 ,
,
![]() .
.
2.9.
 ,
,
![]() .
.
2.10.
 ,
,
![]() .
.
Задача 3. Найти площадь фигуры, ограниченной данными линиями.
3.1.
![]() .
.
3.2.
![]() .
.
3.3.
![]() .
.
3.4.
 .
.
3.5.
![]() .
.
3.6.
![]() .
.
3.7.
![]() .
.
3.8.
![]() .
.
3.9.
![]() .
.
3.10.
![]() .
.
Задача 4. Найти площадь фигуры, заданной неравенствами.
4.1.
 .
.
4.2.
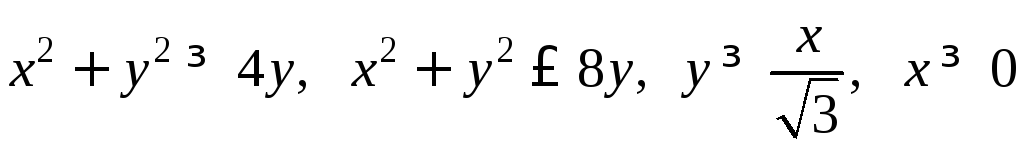 .
.
4.3.
 .
.
4.4.
![]() .
.
4.5.
![]() .
.
4.6.
 .
.
4.7.
![]() .
.
4.8.
![]() .
.
4.9.
![]() .
.
4.10.
![]() .
.
Контрольная работа по теме «Криволинейные интегралы» Теоретическая часть
Существует два вида криволинейных интегралов. По аналогии с обычным определенным интегралом строятся так называемые криволинейные интегралы первого рода. Эти интегралы нашли своё приложение и в геометрии (вычисление площадей цилиндрических поверхностей, длин кривых), и в физике (нахождение массы кривой с переменной плотностью). Но при изучении многих разделов самой математики (дифференциальные уравнения, ТФКП и др.) чаще применяются сведения из теории криволинейных интегралов второго рода.
Поэтому остановимся только на рассмотрении криволинейных интегралов второго рода.
1. Определение криволинейного интеграла второго рода
Пусть
в плоскости (XOY)
задана спрямляемая кривая (АВ)
и вдоль нее
определена функция f(x,y).
Кривую (АВ)
разобьем на
n
частей произвольным образом точками
![]() .
На каждой частичной дуге выберем
произвольно точку
.
На каждой частичной дуге выберем
произвольно точку
![]() .
Обозначим через
.
Обозначим через
![]() и
и
![]() направленные проекции дуги
направленные проекции дуги
![]() на оси координат,
на оси координат,
![]() - длина частичной дуги
- длина частичной дуги
![]() .
Обозначим разбиение через T.
Составим сумму:
.
Обозначим разбиение через T.
Составим сумму:
 .
(1)
.
(1)
Сумма (1) называется интегральной суммой для функции f(x,y) на кривой (АВ) по координате x.
Обозначим
через
![]() -
максимум длин частичных дуг.
-
максимум длин частичных дуг.
Определение
1. Число
I
называется пределом
интегральной суммы
![]() при
при
![]() ,
то есть
,
то есть
![]() ,
если
,
если
![]() :
:
![]() .
.
Определение
2. Если
существует конечный предел интегральной
суммы
![]() при
при
![]() ,
то он называется криволинейным
интегралом по координате x
от функции f(x,y),
взятым по кривой (АВ).
Функция f(x,y)
называется интегрируемой
вдоль кривой
(АВ)
по координате x,
если для нее вдоль этой кривой существует
криволинейный интеграл по x.
,
то он называется криволинейным
интегралом по координате x
от функции f(x,y),
взятым по кривой (АВ).
Функция f(x,y)
называется интегрируемой
вдоль кривой
(АВ)
по координате x,
если для нее вдоль этой кривой существует
криволинейный интеграл по x.
Обозначение:
![]() .
Таким образом, по определению
.
Таким образом, по определению
 .
(2)
.
(2)
Аналогично
определяется криволинейный интеграл
от функции f(x,y)
по координате y,
взятый по кривой (АВ):
Криволинейные интегралы по координатам x и y называются криволинейными интегралами второго рода.
Определение
3. Если
вдоль кривой (АВ)
заданы две функции P(x,y),
Q(x,y),
и существуют
![]() и
и
![]() ,
то сумма этих интегралов также называется
криволинейным
интегралом второго рода (общего вида)
и обозначается:
,
то сумма этих интегралов также называется
криволинейным
интегралом второго рода (общего вида)
и обозначается:
![]() .
.
Замечание.
Если на кривой (АВ)
поменять направление интегрирования
на противоположное, то и знак криволинейного
интеграла второго рода также изменится
на противоположный. Это происходит
потому, что в интегральных суммах

 изменится на противоположный знак
изменится на противоположный знак
![]() (
(![]() ).
Таким образом, криволинейные интегралы
второго рода от одной и той же функции
f(x,y),
взятые по одной и той же кривой (АВ),
но в противоположных направлениях,
равны по модулю, но противоположны по
знаку:
).
Таким образом, криволинейные интегралы
второго рода от одной и той же функции
f(x,y),
взятые по одной и той же кривой (АВ),
но в противоположных направлениях,
равны по модулю, но противоположны по
знаку:
![]()
![]()
![]() .
.
Следовательно, при вычислении криволинейных интегралов второго рода необходимо учитывать направление интегрирования. Из двух направлений по кривой одно считается «положительным», другое - «отрицательным».
Если кривая интегрирования представляет собой простой замкнутый контур, то за «положительное» направление обхода контура принимается направление против часовой стрелки, за «отрицательное» направление - направление по часовой стрелке. В более сложных случаях за «положительное» направление обхода принимается то направление, при котором область, ограниченная этим контуром, остается всё время слева.
Обозначения
интегралов по замкнутому контуру:
![]() ,
,
![]() .
.
