
- •Кандидат физико-математических наук, доцент кафедры математики бгита н.А. Часова
- •Понятие функции нескольких переменных
- •Предел функции. Непрерывность
- •Частные производные и дифференцируемость функции. Дифференциал
- •Производная по направлению. Градиент
- •Производная сложной функции
- •Частные производные и дифференциалы высших порядков
- •Неявные функции
- •Касательная плоскость и нормаль к поверхности
- •Экстремумы функции двух переменных
- •Задачи о наибольших и наименьших значениях
- •Примеры решения задач
- •Задания для самостоятельного решения
- •Интегральное исчисление функций нескольких переменных
- •Контрольная работа по теме
- •«Двойной интеграл и его приложения»
- •Теоретическая часть
- •1. Определение двойного интеграла
- •Геометрический смысл двойного интеграла
- •2. Некоторые свойства двойного интеграла
- •3. Вычисление двойного интеграла повторным интегрированием
- •4. Замена переменных в двойном интеграле
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Контрольная работа по теме «Криволинейные интегралы» Теоретическая часть
- •1. Определение криволинейного интеграла второго рода
- •2. Некоторые свойства криволинейного интеграла второго рода
- •3. Существование и вычисление криволинейных интегралов второго рода
- •4. Формула Грина-Остроградского
- •5. Криволинейные интегралы, не зависящие от пути интегрирования
- •Нахождение функции по ее полному дифференциалу
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Ответы Дифференциальное исчисление функций нескольких переменных
- •Двойной интеграл и его приложения
- •Криволинейные интегралы
- •Литература
2. Некоторые свойства криволинейного интеграла второго рода
Для
краткости формулировок рассмотрим
свойства криволинейного интеграла
только для интеграла по переменной x,
то есть для
![]() .
.
Свойство
1. Если
функция f
интегрируема вдоль кривой (АВ),
![]() ,
то функция
,
то функция
![]() также интегрируема вдоль кривой (АВ)
и справедливо
равенство:
также интегрируема вдоль кривой (АВ)
и справедливо
равенство:
![]() .
.
Свойство
2. Если
функции f
и g
интегрируемы вдоль кривой (АВ),
то функция
![]() также интегрируема вдоль кривой (АВ)
и справедливо
равенство:
также интегрируема вдоль кривой (АВ)
и справедливо
равенство:
![]() .
.
Свойство
3 (аддитивность).
Если функция f
интегрируема вдоль кривой (АВ),
то
![]() функция f
интегрируема вдоль кривых (АС)
и (СВ)
и справедливо равенство:
функция f
интегрируема вдоль кривых (АС)
и (СВ)
и справедливо равенство:
![]()
Свойство 4. Если функция f интегрируема вдоль кривой (АВ), то она интегрируема вдоль кривой (ВА) и справедливо равенство:
![]()
Свойство 5. Если функция f интегрируема по замкнутому контуру (L), то величина криволинейного интеграла не зависит от того, какую точку контура принять за начальную.
3. Существование и вычисление криволинейных интегралов второго рода
Теорема.
Пусть кривая (L)=(AB)
задана параметрическими уравнениями
 ,
,
![]() где
где
![]() ,
,
![]() - непрерывно дифференцируемые функции
на
- непрерывно дифференцируемые функции
на
![]() ,
,
![]()
![]() Пусть функции
Пусть функции
![]() ,
P(x,y),
Q(x,y)
непрерывны на кривой (L).
Тогда существуют интегралы
,
P(x,y),
Q(x,y)
непрерывны на кривой (L).
Тогда существуют интегралы
![]()
![]() ,
,
![]() и справедливы равенства:
и справедливы равенства:
 ;
; 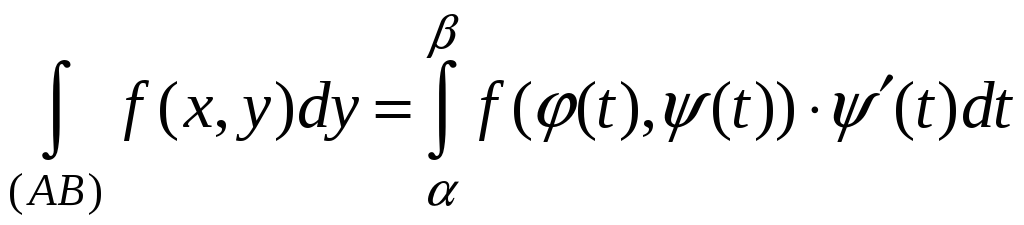 ;
;
 .
.
Замечание
1. Пусть
кривая (АВ)
задана явным уравнением
![]() ,
где функция
,
где функция
![]() непрерывно дифференцируема на отрезке
[a,b],
непрерывно дифференцируема на отрезке
[a,b],
![]() ,
,
![]() .
Тогда если функция f
непрерывна на кривой (АВ),
то справедлива формула:
.
Тогда если функция f
непрерывна на кривой (АВ),
то справедлива формула:
 .
.
Замечание
2. Если
кривая (АВ)
представляет собой прямолинейный
отрезок, параллельный оси OY,
то
![]() .
.
(Это
следует из того, что в интегральных
суммах
![]() .
Тогда
.
Тогда
 и
и
![]() .)
.)
Аналогично,
если кривая (АВ)
есть отрезок, параллельный оси OX,
то
![]() .
.
4. Формула Грина-Остроградского
Формула Грина-Остроградского связывает двойной интеграл по области (P) с криволинейным интегралом по границе (L) этой области.
Область (P) называется простой, если она одновременно является простой областью I типа и II типа. Очевидно, что любая прямая, параллельная осям координат, пересекает простую область не более чем в двух точках.
Теорема.
Пусть (P)
простая область (или область, представимая
в виде конечного числа простых областей),
(L)
- ее контур.
Тогда если P(x,y),
Q(x,y)
непрерывны вместе со своими частными
производными
![]() ,
,
![]() на замкнутой области (P),
то справедлива формула:
на замкнутой области (P),
то справедлива формула:
 (3)
(3)
где интегрирование по контуру (L) ведётся в положительном направлении.
Формула (3) называется формулой Грина-Остроградского.
Из формулы Грина-Остроградского можно вывести формулу для вычисления площади плоской области (P) с границей (L):

где интегрирование по контуру (L) ведётся в положительном направлении.
5. Криволинейные интегралы, не зависящие от пути интегрирования
Все рассматриваемые кривые предполагаются кусочно-гладкими.
Определение 1. Область называется связной, если любые две точки области можно соединить ломаной, целиком лежащей в этой области.
Определение 2. Связная область (D) называется односвязной, если любой замкнутый контур, лежащий в (D), ограничивает область, также целиком лежащую в (D). (Проще: односвязная область не имеет «дыр»).
Пусть
на области (D)
заданы две непрерывные функции P(x,y)
и Q(x,y).
Возьмем любые две точки
![]() и зафиксируем их. Соединим A
и B
всевозможными кривыми (L),
лежащими в области (D).
Тогда интеграл
и зафиксируем их. Соединим A
и B
всевозможными кривыми (L),
лежащими в области (D).
Тогда интеграл
![]() (1)
(1)
будет иметь различные значения в зависимости от кривой (L).
Определение
3. Если
для любых фиксированных точек
![]() значение криволинейного интеграла (1)
по любой кривой, лежащей в области (D)
и соединяющей точки A
и B,
одно и тоже, то говорят, что интеграл
(1) не зависит
от пути интегрирования на области (D).
В этом случае значение интеграла (1)
определяется только заданием точек A
и B.
значение криволинейного интеграла (1)
по любой кривой, лежащей в области (D)
и соединяющей точки A
и B,
одно и тоже, то говорят, что интеграл
(1) не зависит
от пути интегрирования на области (D).
В этом случае значение интеграла (1)
определяется только заданием точек A
и B.
Условия независимости криволинейного интеграла от пути интегрирования на области (D) задаются следующими теоремами.
Теорема 1. Для того чтобы криволинейный интеграл (1) не зависел от пути интегрирования на области (D) необходимо и достаточно, чтобы он был равен нулю по любому замкнутому контуру, лежащем в области (D).
Теорема
2. Пусть
функции P(x,y)
и Q(x,y)
непрерывны вместе со своими частными
производными
![]() и
и
![]() на области (D).
Для того чтобы криволинейный интеграл
(1) на области (D)
не зависел от пути интегрирования
необходимо, а в случае односвязности
области (D)
и достаточно, чтобы во всех точках
области (D)
выполнялось равенство
на области (D).
Для того чтобы криволинейный интеграл
(1) на области (D)
не зависел от пути интегрирования
необходимо, а в случае односвязности
области (D)
и достаточно, чтобы во всех точках
области (D)
выполнялось равенство
![]() .
.
Теорема
3. Пусть
функции P(x,y)
и Q(x,y)
непрерывны на области (D).
Для того чтобы интеграл![]() не зависел от пути интегрирования
необходимо и достаточно, чтобы
подынтегральное выражение
не зависел от пути интегрирования
необходимо и достаточно, чтобы
подынтегральное выражение
![]() являлось полным дифференциалом некоторой
функции F(x,y),
определенной на области (D),
т.е.
являлось полным дифференциалом некоторой
функции F(x,y),
определенной на области (D),
т.е.
![]() .
.
Из теорем 2 и 3 существует важное следствие.
Следствие.
Пусть на односвязной области (D)
функции
![]() непрерывны. Для того чтобы на области
(D)
выражение
непрерывны. Для того чтобы на области
(D)
выражение
![]() было полным дифференциалом некоторой
функции необходимо и достаточно, чтобы
на области (D)
выполнялось следующее условие
было полным дифференциалом некоторой
функции необходимо и достаточно, чтобы
на области (D)
выполнялось следующее условие
![]() .
.
Определение.
Функция F(x,y)
называется
первообразной
дифференциального
выражения
![]()
![]() на области (D),
если на этой области
на области (D),
если на этой области
![]() .
.
Если
F(x,y)
является
первообразной выражения
![]() на области (D),
то
на области (D),
то
![]() также является первообразной для
выражения
также является первообразной для
выражения
![]() ,
то есть выражение
,
то есть выражение
![]() имеет бесконечно много первообразных.
Их общий вид
имеет бесконечно много первообразных.
Их общий вид
![]() .
.
В
ходе доказательства теоремы 3
обосновывается, что одной из первообразных
для выражения
![]() является функция
является функция
 ,
,
где
![]() - некоторая произвольная фиксированная
точка области (D).
- некоторая произвольная фиксированная
точка области (D).
Тогда
общий вид первообразных для выражения
![]() :
:
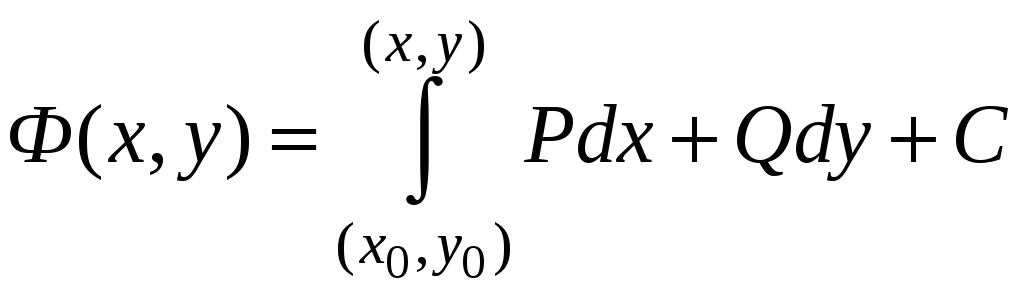 .
.
Заметим, что в этом равенстве интеграл не зависит от пути интегрирования на области (D).
