
- •Кандидат физико-математических наук, доцент кафедры математики бгита н.А. Часова
- •Понятие функции нескольких переменных
- •Предел функции. Непрерывность
- •Частные производные и дифференцируемость функции. Дифференциал
- •Производная по направлению. Градиент
- •Производная сложной функции
- •Частные производные и дифференциалы высших порядков
- •Неявные функции
- •Касательная плоскость и нормаль к поверхности
- •Экстремумы функции двух переменных
- •Задачи о наибольших и наименьших значениях
- •Примеры решения задач
- •Задания для самостоятельного решения
- •Интегральное исчисление функций нескольких переменных
- •Контрольная работа по теме
- •«Двойной интеграл и его приложения»
- •Теоретическая часть
- •1. Определение двойного интеграла
- •Геометрический смысл двойного интеграла
- •2. Некоторые свойства двойного интеграла
- •3. Вычисление двойного интеграла повторным интегрированием
- •4. Замена переменных в двойном интеграле
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Контрольная работа по теме «Криволинейные интегралы» Теоретическая часть
- •1. Определение криволинейного интеграла второго рода
- •2. Некоторые свойства криволинейного интеграла второго рода
- •3. Существование и вычисление криволинейных интегралов второго рода
- •4. Формула Грина-Остроградского
- •5. Криволинейные интегралы, не зависящие от пути интегрирования
- •Нахождение функции по ее полному дифференциалу
- •Примеры решения задач
- •Задачи для самостоятельной работы
- •Ответы Дифференциальное исчисление функций нескольких переменных
- •Двойной интеграл и его приложения
- •Криволинейные интегралы
- •Литература
Интегральное исчисление функций нескольких переменных
Контрольная работа по теме
«Двойной интеграл и его приложения»
Теоретическая часть
Переходя к интегральному исчислению функций нескольких переменных, условимся, что в дальнейшем будем пользоваться такими фигурами (Р) и телами (V), которые имеют площади и объемы соответственно.
Напомним, что:
1. если контур области (Р) состоит из конечного числа непрерывных кривых, каждая из которых выражается явным уравнением вида
y=f(x) или x=g(y)
где y=f(x) и x=g(y) – непрерывные функции на соответствующих промежутках, то область (Р) квадрируема, то есть имеет площадь;
2. если граница тела (V) может быть разбита на конечное число частей, каждая из которых есть поверхность, определённая одним из уравнений
![]()
где
функции
![]() непрерывны на соответствующих замкнутых
областях, то тело (V)
кубируемо,
то есть имеет объём.
непрерывны на соответствующих замкнутых
областях, то тело (V)
кубируемо,
то есть имеет объём.
1. Определение двойного интеграла
Пусть
на замкнутой квадрируемой области (P)
задана функция z=f(x,y).
Построим разбиение Т
области (P)
сетью кривых
на п
частичных квадрируемых областей
![]() ,
площади которых обозначим
,
площади которых обозначим
![]() соответственно. В каждой частичной
области (Pk)
произвольно выберем точку
соответственно. В каждой частичной
области (Pk)
произвольно выберем точку
![]() и вычислим значение функции в этой
точке
и вычислим значение функции в этой
точке
![]() .
Составим сумму
.
Составим сумму
 ,
(1)
,
(1)
которую
будем называть интегральной
суммой для функции f
на области (P),
соответствующей данному разбиению Т
и выбору точек
![]() .
.
Диаметром
замкнутой области (Р)
называется наибольшее расстояние между
двумя точками её границы. Пусть
![]() - диаметр области
- диаметр области
![]() .
Обозначим
.
Обозначим
![]() .
.
Определение
1. Если
существует конечный предел интегральной
суммы (1) при
![]() ,
не зависящий ни от способа разбиения
Т,
ни от выбора точек
,
не зависящий ни от способа разбиения
Т,
ни от выбора точек
![]() ,
то этот предел
называется двойным
интегралом от функции f(x,y) по области
(Р)
и обозначается
,
то этот предел
называется двойным
интегралом от функции f(x,y) по области
(Р)
и обозначается
![]() .
.
Функция z=f(x,y) в этом случае называется интегрируемой на области (P).
Таким образом, по определению
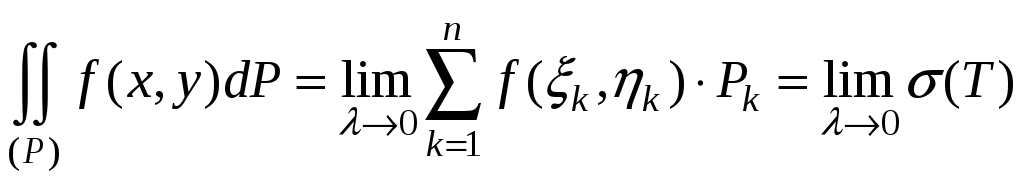 . (2)
. (2)
Символ
dР
называют элементом
площади. В
прямоугольных координатах dР=dxdy.
(Такое представление dP
можно объяснить тем, что если разбиение
фигуры (P)
осуществить
прямыми, параллельными координатным
осям, то площадь частичной области
запишется в виде произведения
![]() .)
.)
Геометрический смысл двойного интеграла
1. Двойной интеграл от неотрицательной, непрерывной функции f(x,y) геометрически выражает собой объём цилиндрического бруса, ограниченного сверху поверхностью z=f(x,y), снизу – плоскостью XOY:
![]()
причём (P) – это проекция цилиндрического бруса на плоскость XOY.
2. Если положить f(x, y)=1 всюду на области (P), то получим:

Таким образом, площадь плоской области (P) равна двойному интегралу от единицы по этой области:
![]() (3)
(3)
Теорема 1.1 (необходимое условие интегрируемости). Если функция z=f(x,y) интегрируема на области (Р), то она ограничена на этой области.
Теорема 1.2 (достаточное условие интегрируемости). Если функция z=f(x,y) непрерывна на замкнутой квадрируемой области (Р), то она интегрируема на этой области.
