2.2.Основные свойства функций

1. Ограниченность

Определение 1. Функция , заданная на множестве , называется ограниченной сверху (снизу) на этом множестве, если существует такое число , что для всех выполняется неравенство ():

.

Определение 2. Функция называется ограниченной на множестве , если существует такое , что для всех :

.

Пример 1. Докажем, что функция ограничена.

Решение. Так как , то для любого выполняются неравенства . Значит функция ограничена на .

При доказательстве ограниченности функций оказываются полезными следующие утверждения:

а) Если функция ограничена на множествах и , то она ограничена и на объединении этих множеств.

б) Если функции и ограничены на множестве , то их сумма и произведение ограничены на .

в) Если функция ограничена на множестве сверху, то ограничена на снизу.

г) Если функция положительна на и ограничена на снизу положительным числом, то функция ограничена на .

Пример 2. Докажем, что функции и ограничены на отрезке .

Решение. Функция ограничена на , так как на этом отрезке выполняется неравенство . Постоянные функции и также ограничены на . Заданную функцию можно представить как сумму произведений ограниченных функций: , а тогда по утверждению б) функция ограничена на . Так как значения функции на не меньше, чем 3, и она ограничена, то по утверждению г) функция ограничена на .

Сформулируем теперь отрицания введенных понятий.

Определение 3. Функция

– неограниченна сверху на : ;

– неограниченна снизу на : ;

– неограниченна на : .

Пример 3. Докажем, что функция не является ограниченной на .

Решение. Возьмем произвольное и докажем, что существует , такое, что , т.е. . Это и будет означать неограниченность функции на . Возьмем . Тогда . Неограниченность функции доказана. Заметим, что на любом интервале , где , эта функция ограничена: если , то .

Пример 4. Докажем, что функция , , не ограничена.

Решение. При , , имеем , и потому принимает сколь угодно большие значения.

Если функция ограничена на множестве , то множество ее значений на имеет точную верхнюю и точную нижнюю грани. Их обозначают и . Индекс обычно опускают. Числа и могут как принадлежать, так и не принадлежать множеству значений функции.

Пример 5. Для функции , , имеем , . Значения 1 и –1 принадлежат множеству значений функции.

Пример 6. Для функции , , имеем , . Значение 0 функция принимает при . Значение 1 эта функция не принимает ни при каком . Но среди значений функции есть сколь угодно близкие к 1. Так, при имеем . Это значение отличается от 1 меньше чем на 0,000004.

2. Монотонность

Определение 4. Функция называется:

– возрастающей на : ;

– убывающей на : ;

– неубывающей на : ;

– невозрастающей на :

При движении вдоль оси абсцисс слева направо ордината графика возрастающей функции увеличивается (рис. 1), а ордината графика убывающей функции уменьшается (рис. 2).

Графики неубывающей функции (рис. 3) и невозрастающей функции (рис. 4) могут иметь «площадки».

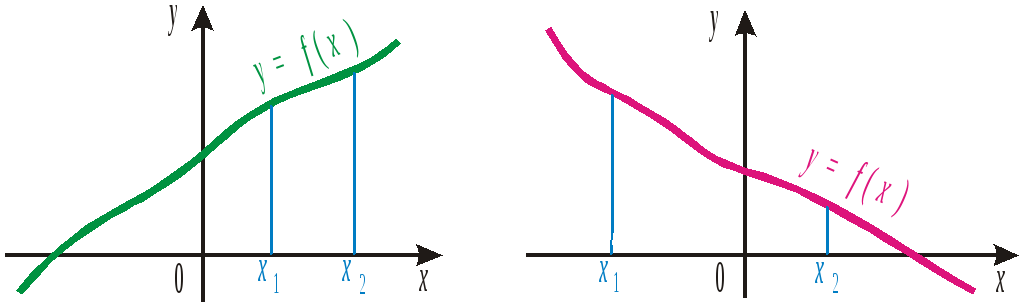
Рис. 1 Рис. 2

Рис. 3 Рис. 4

Если функция возрастает (убывает, не возрастает, не убывает) на , то говорят, что она монотонна на .

Пример 7. Докажем, что функция возрастает на всей числовой прямой.

Решение. Пусть . Тогда

.

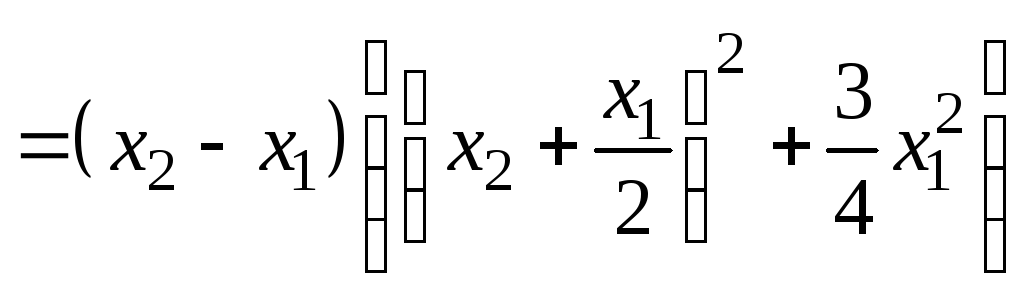Так как и то Итак, . Значит функция возрастает на всей числовой прямой.

Пример 8. Докажем, что функция возрастает на отрезке .

Решение. Пусть . Тогда

.

Так как , , , то , а так как , , то . Значит, , а потому . С другой стороны, из получаем, что , и потому . Но тогда и , т.е. возрастает на отрезке .

При исследовании функций на монотонность бывают полезны следующие утверждения:

а) Если функции и возрастают (убывают) на множестве , то их сумма возрастает (убывает) на этом множестве.

б) Если функция возрастает (убывает) на множестве , то функция возрастает (убывает) на этом множестве.

в) Если функции и неотрицательны на множестве и возрастают (убывают) на этом множестве, то их произведение возрастает (убывает) на множестве .

г) Если функция положительна на множестве и возрастает (убывает) на этом множестве, то функция возрастает (убывает) на множестве .

д) Если функция возрастает (убывает) на множестве , а функция возрастает (убывает) на множестве , то их композиция возрастает (убывает) на множестве .

Пользуясь утверждениями а) – д), легко доказать, что разность возрастающей и убывающей функций возрастает, а также, что функция , где и положительны, возрастает, а убывает на , является возрастающей функцией на . Отметим еще, что прибавление к функции любого числа, а также умножение функции на любое положительное число не изменяют характера монотонности этой функции.

Сформулируйте самостоятельно утверждения аналогичные а) – д) для неубывающих и невозрастающих функций.

Пример 9. Докажем, что функция () возрастает на .

Решение. Функция является произведением функций, каждая из которых равна . Так как множители неотрицательны и возрастают на , то и функция () возрастает на .

Пример 10. Докажем, что на функция () при четном убывает, а при нечетном возрастает.

Решение. Если , то , и потому . Если четно, то отсюда получаем, что , чем доказано убывание функции на . Если же нечетно, то получаем, что , т.е. что , и потому при нечетном функция возрастает на .

Пример 11. Докажем, что функция возрастает на .

Решение. Данная функция является суммой числа 4 и функций , , возрастающих на , а потому она возрастает на .

Пример 12. Докажем, что функция () возрастает на .

Решение. Пусть . Из следовало бы, что , т.е. вопреки предположению. Значит , а потому функция () возрастает на .

Пример 13. Докажем, что функция возрастает на .

Решение. Данная функция является композицией функций и , причем возрастает на и принимает значения от 4 до , а функция возрастает на . Поэтому функция возрастает на от до .