§2. Функциональные отношения

n1. Понятие функции

Напомним «школьное» определение функции, являющееся центральным понятием математики. «Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у». (См. Ю.М. Макарычев и др. Алгебра 9: Учебник для 9 классов средней школы / Под ред. С.А. Теляковского – М: Просвещение, 1992).

Это определение требует существенных уточнений.

Например, не ясно, что понимается под словами: «зависимость» и «соответствует».

Понятие отношение позволяет уточнить данное определение функции.

Определение 1. Отношение f между элементами множества Х и Y называется функциональным или функцией (или отображением множества Х во множество Y, или функцией, определенной на Х со значением в Y), если выполняется требование: хХ !yY (x f y), то есть при отношении f каждому х из Х сопоставляется единственное значение у из Y.

Если f – функциональное отношение между элементами множеств Х и Y, то:

1) переменная х со значениями из Х называется независимой переменной или аргументом функции f;

2) переменная у с множеством всех значений Y называется зависимой переменной функции f;

3) если х₀ f y₀ , то у₀ обозначается символом f(x₀) и называется значением функции f при х=х₀ или образом х₀ при отображении f.

4) наряду с обозначением f для функционального отношения между элементами X и Y используются так же следующие символы: ХY, f: XY, f: xf(x) (символ – «ограниченная» стрелка).

На случай функционального отношения переносятся понятия области отправления, области прибытия, области определения, области значений, графа и графика отношения f.

Заметим, что для функции f: ХY имеет место равенство D(f)=X. Отношение, рассмотренное в примере 1 (2) не является функциональным, хотя бы по той причине, что область отправления и область определения этого отношения не совпадают.

Если Х и Y – конечные множества, то функцию f: XY можно проиллюстрировать с помощью графа отношения:

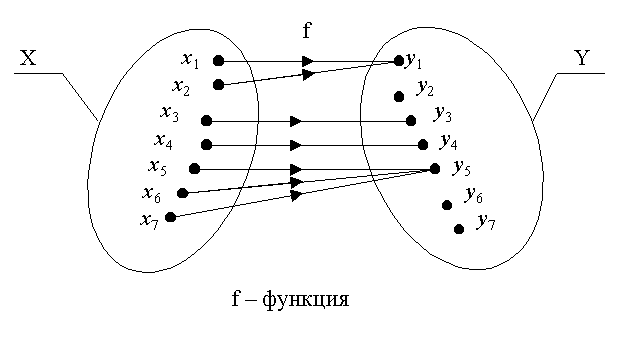
Отношение f между элементами множеств Х и Y является функциональным тогда и только тогда, когда из каждой точки, изображающей элемент множества Х, выходит одна и только одна стрелка графа этого отношения.

Определение 2. Пусть f: XY – некоторое отображение; X₀X, Y₀Y, x₀X, y₀Y. Если у₀=f(x₀), то х₀ называется прообразом элемента у₀ при отображении f.

Множества f(X₀){f(x)xX₀}, f^–1(Y₀)={xxX  f(x)Y₀} и f^–1({y₀})={xxXf(x)=y₀} называются соответственно образом множества Х₀, прообразом множества Y₀ и полным прообразом элемента у₀ при отображении f.

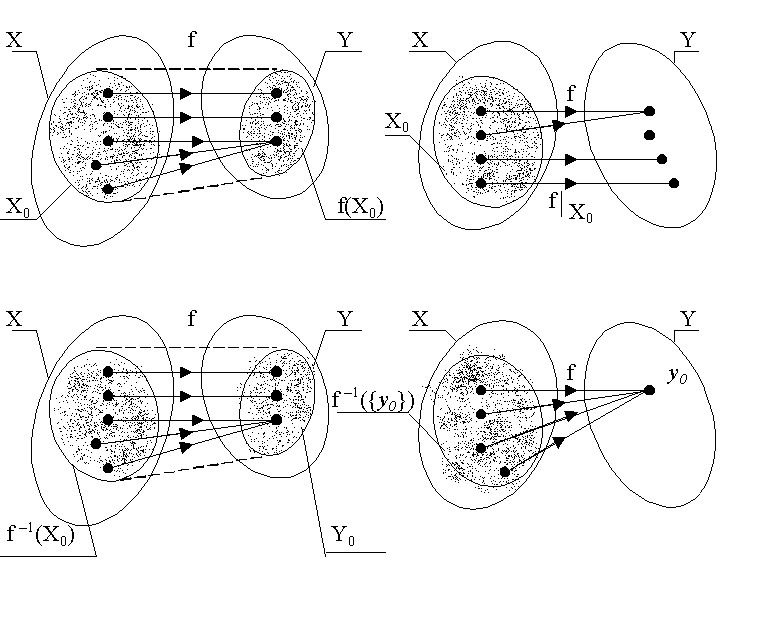
Если Х₀, то отображение множества Х₀ во множества Y, обозначаемое символом ^f_X0 и задаваемое условием хХ₀ (^f_X0 (х)=f(x)) называется сужением функции f на множестве Х₀.

Проиллюстрируем введенные понятия с помощью графа отображения f: XY для случая, когда Х и Y – конечные множества.

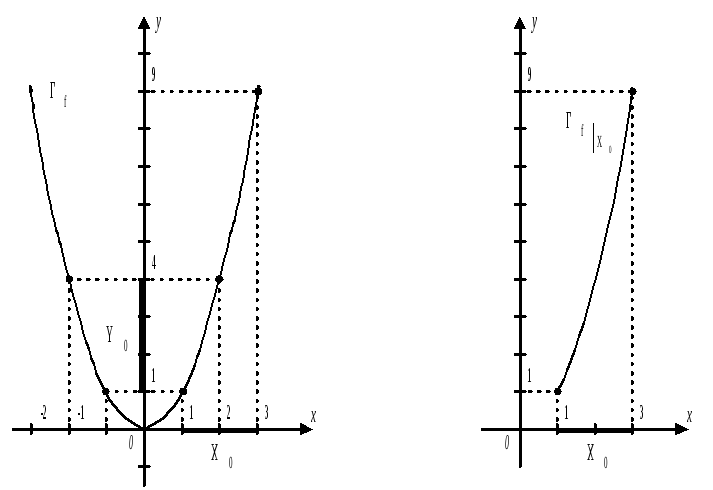
Пример 1. Пусть Х=R; Y=[0; +]; Х₀=[1; 3]; Y₀=[1; 4]; y₀=4; G={(x,y)R²y=x²}. Тогда f=(G, X, Y) – функциональное отношение между элементами множеств X и Y, причем f(X₀){f(x) | 1x3}=[1; 9], f^–1(Y₀)={x | 1f(x)4}=[–2; –1][1; 2], f ^–1({4})=[–2; 2]. Функция ^f_X0= ^f_{[1; 3]} возрастает на своей области определения [1; 3], причем Е (^f_X0)=[1; 9].

n2. Инъективные, сюрьективные и биективные функции.

Функция, обратная для данной

Определение 3. Пусть f: XY. Данная функция называется:

1) инъективной, если верно утверждение

х₁X х₂X (х₁х₂  f(x₁)  f(x₂));

2) сюрьективной, если верно утверждение

уY хX (f(x)=y), то есть E(f)=Y;

3) биективной (взаимно однозначным отображением X в Y, биекцией, или взаимно однозначным соответствием между элементами множеств Х и Y), если f является одновременно инъективной и сюрьективной.

Если f: XY – биекция, то множества Х и Y называются равномощными или эквивалентными. Множество равномощное множеству N называется счетным.

По правилу контрапозиции функции f: XY является инъективной тогда и только тогда, когда х₁X х₂X (f(x₁)=f(x₂)  х₁=х₂).

Заметим, что функция f является инъективной, если она является возрастающей или убывающей.

Можно убедиться, что конечные множества Х и Y являются равномощными тогда и только тогда, когда n(X) = n(Y); всякое бесконечное множество имеет счетное подмножество; множество [0;1] не является счетным.

Проиллюстрируем введенные понятия для случая функции f: XY, когда Х и Y – конечные множества:

П ример 2. Для функции f из примера 1 имеем f(X)=[0; +)=Y, однако f(–2)=f(2). Следовательно, f является сюрьективной, но не инъективной.

Пример 3. Пусть X=R, Y=(0; +), G={(x, y) | xX  y=2^x}. Тогда f =(G, X, Y) – функция. Так как f – возрастающая функция и E(f)=(0; +)=Y, то f является инъективной и сюрьективной, биекцией. (Отсюда следует, что R и (0; +) – равномощные множества).

Если f = (G, X, Y) – биекция, то отношение

({(y, x) | (x, y)G}, Y, X) (1)

является функцией, причем инъективной и сюрьективной, то есть биекцией.

Определение 4. Для биекции f=(G, X, Y) функция (1) называется обратной и обозначается символом f ^-1.

Приведем иллюстрацию введенного понятия для случая биекции f: XY, когда Х и Y – конечные множества:

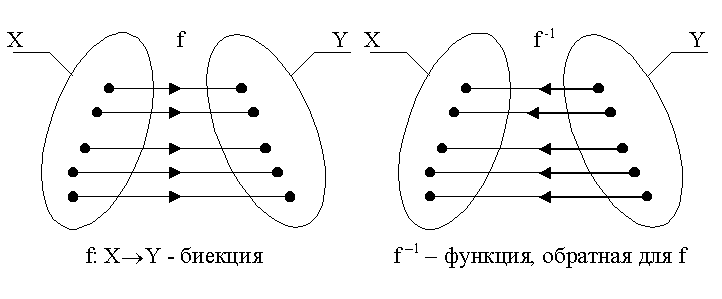
Из сказанного выше и определения функции, обратной для биекции f: XY следуют утверждения:

1. Функция f ^–1 является биекцией.

2. Функция  является обратной для биекции f тогда и только тогда, когда: : YX  xX yY ((y)=x  f(x)= y).

3. Биекция f в свою очередь является обратной для f ^–1, то есть имеет место равенство (f ^–1)^–1 = f.

4. Если независимые переменные функций f и f ^–1 обозначаются привычным образом – символом х, а зависимые переменные – символом у, то графики этих функций на координатной плоскости (0ху) связаны следующим образом:

Г_f–1 = {M (в; а) | M(а; в)Г_f}, то есть графики функций f и f ^–1 симметричны относительно прямой у = х.

Пример 4. Функция f: x2^x, определенная на R со значениями в (0; +), рассмотренная в примере 3, является биекцией. Так как хR   у=2^х  у(0; +)  х=log₂ y, то f ^–1: ylog₂y – функция, определенная на (0; +) со значениями в R, являющаяся биекцией.

Обозначая аргумент функции f ^–1 символом х, можем утверждать, что графики функций f: x2^x и f ^–1: xlog₂x на координатной плоскости (0ху) симметричны относительно прямой у=х.

n3. Сложные функции

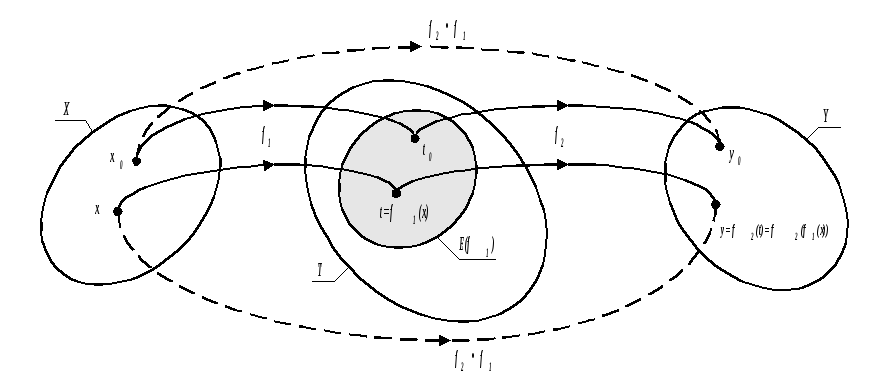
Определение 5. Пусть f₁: XT₀ и f₂: TY – какие-либо функции, причем E(f₁)T. Тогда функция определенная на Х со значениями в Y, сопоставляющая каждому элементу х из Х элемент f₂(f₁(x)) называется сложной функцией (суперпозицией или композицией функций f₁ и f₂) и обозначается символом f₂ f₁.

Итак, если f₁ и f₂ – функции из определения 5, то f₂f₁: XY и f₂f₁: xf₂(f₁(x)). Для случая, когда X, Y, T₀ – конечные множества функцию f₂f₁ можно проиллюстрировать следующим образом:

Пример 5. Функцию f: x, определенную на [0; +) со значениями из R можно рассматривать как композицию f₂f₁ функции f₁: x, определенной на [0; +) со значениями [0; +), и функции f₂: tsin t, определенную на R со значениями в R (существенно, что E(f₁)D(f₂)).

Итак, f = f₂  f₁:

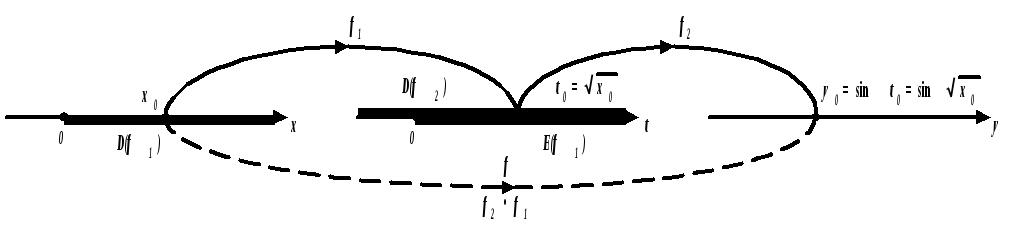
Заметим, что из возрастания функции f₁ на [0; ²/4], возрастания функции f₂ на [0; /2] и равенства f₁ ([0; ²/4]) = f₂ ([0; /2]) можно сделать вывод о возрастании функции f на [0; ²/4].

Введенное понятие композиции двух функций естественно переносится на случай любого конечного числа функций.

Сформулируем так называемое свойство ассоциативности композиции функций: если определена композиция функций f₁, f₂ и f₃, то имеет место равенство f₃  (f₂  f₁) = (f₃  f₂)  f₁.

n4. Преобразование данного множества

Из школьного курса геометрии известны понятия преобразования плоскости: движения, параллельного переноса, и т.д. Обобщим эти понятия на случай произвольного множества.

Определение 6. Любая биекция f: XX называется преобразованием множества Х. Преобразование е: хх множества Х называется тождественным.

Если f, f₁, f₂, f₃ – некоторые преобразования множества Х, то:

1. f ^–1 и f₂  f₁ – преобразования множества Х;

2. f₃  (f₂  f₁) = (f₃  f₂)  f₁;

3. f  e = e  f = f;

4. f ^–1  f = f  f ^–1 = e;

5. (f₂  f₁)^–1 = f ₁^–1  f₂^–1.