
- •Кафедра геометрии
- •Вводный курс математики
- •Печатается по решению редакционно-издательского совета университета
- •Содержание
- •Введение
- •Глава 1 элементы теории множеств
- •§1. Понятие множества
- •Будем считать, что множество a задано, если задано правило, позволяющее для каждого объекта а ответить на вопрос: какое из данных утверждений верно аa или aa.
- •§2. Сравнение двух множеств.
- •§3. Кортежи и декартовы произведения множеств
- •Глава 2 элементы математической логики
- •§1. Высказывание и логические операции
- •§2. Логические формулы и их равносильности
- •§3. Предикаты и кванторы
- •§4. Типы теорем. О некоторых методах доказательств теорем
- •Глава 3 отношения и функции
- •§1. Понятие отношения между элементами данных множеств
- •§2. Функциональные отношения
- •§3. Бинарные отношения между элементами данного множества. Отношения эквивалентности
- •Минимум
- •I. Множества и операции над ними
- •II. Высказывания и предикаты
- •III. Отношения и функции
- •Приложение 2 вопросы к зачету по «Вводному курсу математики»
- •Греческий алфавит
- •Латинский алфавит
- •Некоторые стандартные обозначения
- •Литература
§3. Кортежи и декартовы произведения множеств
n1. Понятие кортежа
Понятие кортежа будем считать основным, неопределяемым (слово кортеж происходит от французского слова «cortege» – торжественное шествие). Ограничимся интуитивным описанием этого понятия.
Пусть имеем объекты: а1, а2, …, аn, среди которых могут быть совпадающие, при этом, исходя из некоторых соображений, объект а1 считается 1-ым, объект а2 считается 2-ым, и так далее, наконец объект аn считается n-ым. Тогда будем говорить, что имеем кортеж или упорядоченный набор (а1; а2; …; аn) длины n, называя объекты а1, а2, …, аn соответственно 1-ой, 2-ой, …, n-ой компонентами этого кортежа. Кортежи длины 2 иногда называют парами, длины 3 – тройками, длины 4 – четверками, и так далее.
(а1; а2;…; аn) = (в1; в2;…; вn) тогда и только тогда, когда а1=в1 и а2=в2 и ... и ап=вп.
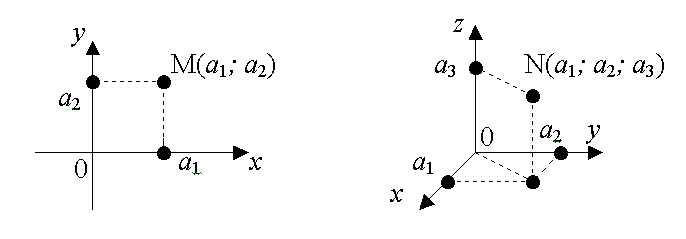
Если а1, а2, а3 – числа, то пару (а1; а2) можно изобразить точкой M(а1; а2) на координатной плоскости (0xy), а тройку (а1; а2; а3) можно изобразить точкой N(а1; а2; а3) в пространственной системе координат (0xyz).
n2. Декартовы произведения множеств
Определение 4. Пусть А1, А2, … Аn, где nN и n>1, – некоторые непустые множества. Декартовым произведением данных множеств называется множество, обозначаемое символом А1А2…Аn и состоящее из всевозможных кортежей вида (а1, а2, …, аn), где а1А1, а2А2, … , аnAn. Если А1=А2=…=An=А, то вместо символа А1А2…An иногда используется символ An, причем множество An называется n-ой декартовой степенью множества А. Множества А2 и А3 называется еще декартовым квадратом и кубом множества А соответственно.
Итак,
А1А2
…An![]() {(а1;
а2;
…; аn)
| а1А1
и а2А2
и … и аnAn}.
{(а1;
а2;
…; аn)
| а1А1
и а2А2
и … и аnAn}.
Если А1, А2, А3 – числовые множества, то множество А1А2 можно изобразить на координатной плоскости (0ху) множеством {M(х; у) | хА1 и уА2}, а множество А1А2А3 можно изобразить множеством {M(х; у; z)| хА1 и уА2 и zА3} в пространственной системе координат (0xyz).
Пример. Найти АВ, если 1) А = {m; n; q} и В = {; }; 2) А=[2;3] и В=[1; +].
Решение.
1) АВ![]() {(а;
в) | аА
и вВ}
= {(m;
); (m;
);
(n;
);
(n;
);
(q;
); (q;
)}.
{(а;
в) | аА
и вВ}
= {(m;
); (m;
);
(n;
);
(n;
);
(q;
); (q;
)}.
2) АВ![]() {(а;
в) | 2a3
и в1}.
Так как A
и B
– числовые множества, то декартово
произведение AB
можно изобразить на координатной
плоскости (0ху)
множеством {M(х;
у) | хA
и
уB},
то есть множеством {M(х; у)
| 2х3
и у1}.
Сравнивая AB
с множеством BA
= {(а; в)
| а1
и 2в3},
убеждаемся, что ABBA.
Действительно, например, (2; 4)(АВ),
но (2; 4)(ВА).
{(а;
в) | 2a3
и в1}.
Так как A
и B
– числовые множества, то декартово
произведение AB
можно изобразить на координатной
плоскости (0ху)
множеством {M(х;
у) | хA
и
уB},
то есть множеством {M(х; у)
| 2х3
и у1}.
Сравнивая AB
с множеством BA
= {(а; в)
| а1
и 2в3},
убеждаемся, что ABBA.
Действительно, например, (2; 4)(АВ),
но (2; 4)(ВА).
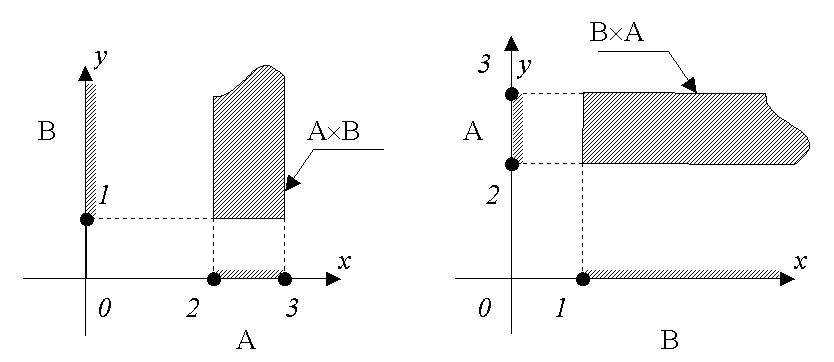
Как следует из рассмотренного выше примера, декартово произведение двух множеств не обладает свойством коммутативности.
n3. Размещения с повторениями и без повторений
Определение 5. Пусть X – данное n-элементное множество. Любой кортеж длины k, где k, nN, компоненты которого принадлежат множеству Х, называется размещением с (возможными) повторениями из n элементов множества Х по k. Любой кортеж длины k, где k, nN, k≤n, компоненты которого попарно различны и принадлежат множеству Х, называется размещением без повторений из n элементов множества Х по k. Всякое размещение без повторений n элементов множества Х по n называется еще перестановкой без повторений n элементов множества Х.
Символами
![]() ,
,
![]() ,
Pn
обозначаются соответственно число всех
размещений с (возможными) повторениями
из n
элементов по k,
число всех размещений без повторений
из n
элементов по k
и число всех перестановок без повторений
n
элементов множества Х.
,
Pn
обозначаются соответственно число всех
размещений с (возможными) повторениями
из n
элементов по k,
число всех размещений без повторений
из n
элементов по k
и число всех перестановок без повторений
n
элементов множества Х.
Согласно этому определению семейство всех размещений с (возможными) повторениями из n элементов множества Х по k совпадает с декартовой степенью Хk и включает в себя семейство всех размещений без повторений из n элементов множества Х по k.
Если
n,
kN,
то имеет место формула:
![]() =
nk.
=
nk.
Если
же n,
kN
и kn,
то
![]() =
n
(n–1)(n–k+1).
=
n
(n–1)(n–k+1).
Полагая
в последней формуле k=n,
получаем формулу для вычисления общего
числа перестановок без повторений n
элементов множества Х:
Рn=![]() =n(n–1)(n–2)…21=n!,
то есть Рn=
n!
(для натурального числа n
произведение 123…(n–1) n
обозначается символом n!
и называется n-факториалом;
например, 5!
=n(n–1)(n–2)…21=n!,
то есть Рn=
n!
(для натурального числа n
произведение 123…(n–1) n
обозначается символом n!
и называется n-факториалом;
например, 5!
![]() 12345=120).
12345=120).
Пример.
Для
множества Х={;
;
;
;
}
привести примеры размещений с (возможными)
повторениями и без повторений, перестановки
его элементов. Вычислить
![]() ,
,
![]() и Р5.
и Р5.
Решение. ( ; ; ; ; ; ; ), (; ; ) – размещения с (возможными) повторениями из 5-ти элементов множества Х по 6 и 3 соответственно.
(; ; ; ), (; ; ) – размещение без повторений из 5-ти элементов множества Х по 4 и 3 соответственно.
(; ; ; ; ) и ( ; ; ; ; ) – перестановки без повторений данных 5-ти элементов множества X.
По
приведенным выше формулам находим, что
![]() =53=125,
=53=125,
![]() =54(5–3+1)=543=60
и Р5=5!=12345=120.
=54(5–3+1)=543=60
и Р5=5!=12345=120.
