Задачи для самостоятельного решения

36. Установить взаимное расположение прямой и плоскости :

а) , ;

б) , .

37. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .

38. Найти угол между прямой и плоскостью .

39. При каком значении параметра прямая параллельна (перпендикулярна) плоскости ?

3.8. Кривые второго порядка

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Каноническое уравнение окружности радиуса R c центром в точке :

. (3.39)

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначаемая через 2а), большая, чем расстояние между фокусами.

Каноническое уравнение эллипса с центром в начале координат (рис.4):

. (3.40)

З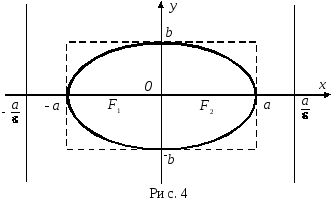 десь – большая полуось, b – малая полуось , точки – фокусы эллипса, .

Эксцентриситет эллипса:

.

Уравнения директрис эллипса:

, .

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначаемая через 2а), меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы с центром в начале координат (рис. 5):

. (3.41)

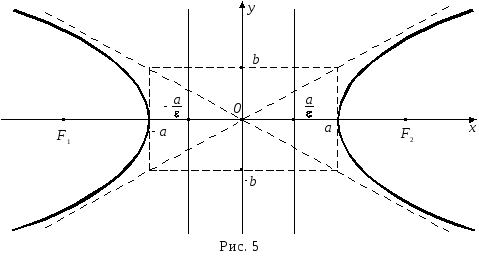
Здесь а – действительная полуось, – мнимая полуось, точки , – фокусы гиперболы, .

Эксцентриситет гиперболы:

.

Уравнения директрис гиперболы:

, .

Уравнения асимптот гиперболы:

, .

Параболой называется множество точек плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Каноническое уравнение параболы с вершиной в начале координат (рис. 6):

. (3.42)

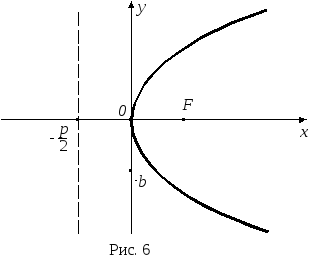
Точка – фокус параболы.

Эксцентриситет параболы .

Уравнение директрисы параболы:

.

Эллипс, гипербола, парабола обладают общим свойством: отношение расстояния r произвольной точки кривой до фокуса к расстоянию d этой точки до соответствующей директрисы есть величина постоянная, равная эксцентриситету кривой, т. е. .

Примеры

15. Найти каноническое уравнение линии, для каждой точки которой отношение расстояния от точки (фокус) к расстоянию до прямой (директриса) есть величина постоянная, равная (эксцентри-ситет). Определить вид линии, сделать чертеж.

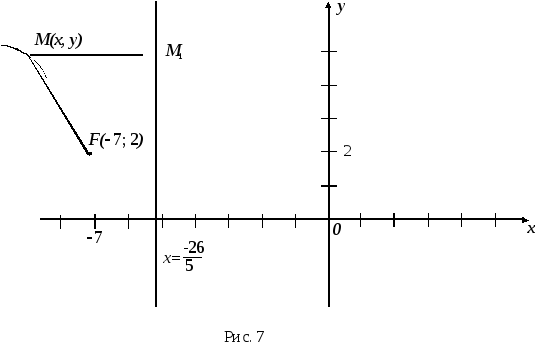
Р е ш е н и е. Сделаем условный чертеж (рис. 7). В выбранной системе координат построим директрису, заданную уравнением , и фокус .

Так как по условию эксцентриситет , то искомой линией будет являться гипербола, и поскольку директриса параллельна оси ОУ, то ее каноническое уравнение будет иметь вид:

. (3.43)

В этом случае точка – центр гиперболы,

а – действительная полуось,

b – мнимая полуось.

Примечания:

1. Если , то искомой линией будет являться эллипс с каноническим уравнением .

2. Если , то искомой линией будет являться парабола с канони-ческим уравнением .

Пусть – произвольная точка гиперболы, МF – расстояние от точки М до фокуса F; MM₁ – расстояние от точки М до директрисы. Тогда по условию задачи

или . (3.44)

Вычислим MF и ММ₁:

,

.

Подставив найденные выражения в уравнение (3.44), получим:

.

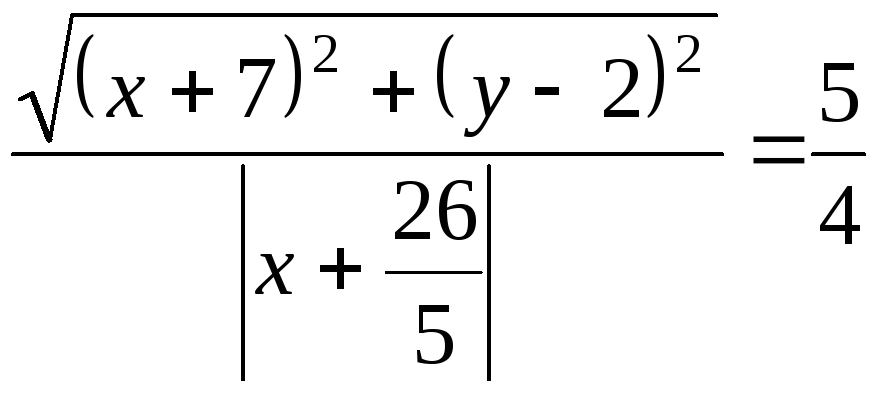Преобразуем полученное уравнение к виду (3.43). Для этого возведем обе части уравнения в квадрат, избавимся от знаменателя и приведем подобные члены. Получим:

,

,

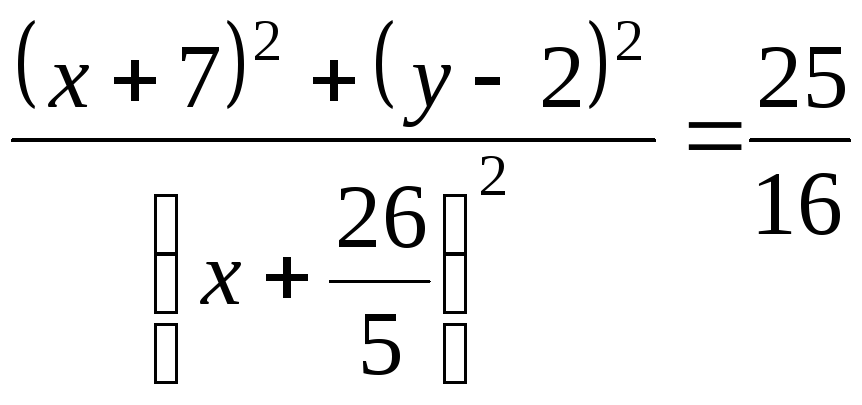Выделим полный квадрат в первой скобке по переменной х и произведем равносильные преобразования:

Разделив обе части уравнения на 144, получим:

или – каноническое уравнение гиперболы с центром в точке , – действительная полуось, – мнимая полуось. Сделаем чертеж.

На рис. 8 – новая система координат с началом в точке .

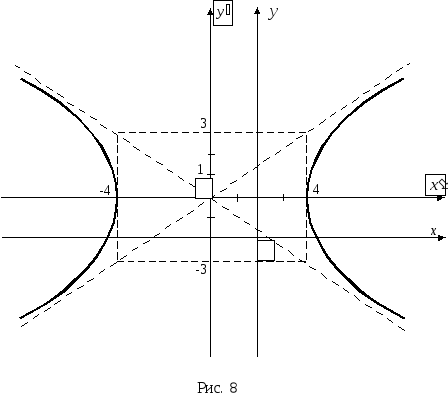
16. Исследовать, какая линия определяется уравнением

.

Р е ш е н и е. Сгруппируем слагаемые, содержащие одну и ту же переменную, и получим

В каждой из скобок выделим полный квадрат:

или

.

Разделив обе части этого уравнения на , получим канонический вид данного уравнения:

.

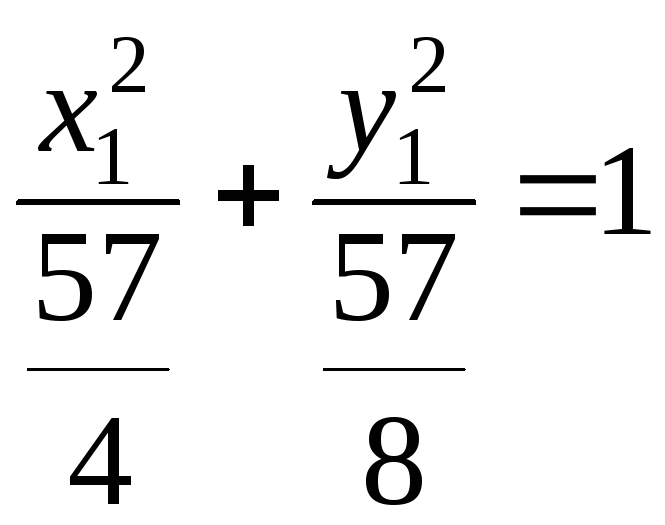Это уравнение определяет эллипс с полуосями центр эллипса находится в точке .