
5. Квадрагиперболическое пространство
Геометрическая структура квадрагиперболического пространства во многом уникальна и тесно связана с метрической функцией Бервальда-Моора. Это заставляет некоторых физиков вполне обоснованно думать о нем, как одной из возможных альтернатив пространству Минковского [11]. Непрерывная группа вращений квадрагиперболического пространства, оставляющая инвариантной его фундаментальную метрическую форму - трехпараметрическая и коммутативная. Казалось бы, только этих двух фактов достаточно, чтобы навсегда отмести данное пространство, как возможную теоретическую основу реального мира, ведь аналогичная группа пространства Минковского, то есть группа Лоренца, шестипараметрическая и некоммутативная. Однако, если критически подойти к имеющимся у физиков экспериментальным сведениям по вопросу качественных свойств реального пространства-времени, приходится признать, что на самом деле таких данных нет, и в принципе быть не может. Ведь для экспериментальной проверки факта некоммутативности группы вращений обычного трехмерного пространства приходится в неявной форме прибегать к дополнительному измерению, повторяя эксперимент во времени и сравнивая между собой результаты различных комбинаций. Чтобы провести аналогичный эксперимент с четырехмерным пространством потребовались бы наблюдатели, имеющие в запасе минимум еще одно, пятое, измерение, оперируя в котором они могли бы сравнить результаты нескольких серий последовательно проведенных преобразований. Следует ли подчеркивать, что если в нашем мире такие наблюдатели и есть, то это явно не мы.
Таким образом, убежденность в шестипараметричности группы вращений нашего физического мира не экспериментальный факт, а скорее экстраполяция предположения, что трехмерное евклидово пространство является составной частью реального пространства событий. Наверное, излишне напоминать об опасности абсолютизации каких бы то ни было предположений, а уж геометрических в особенности. В любом случае, даже если наша попытка увидеть за квадрагиперболическими числами альтернативу пространству Минковского окажется и безуспешной, она, как минимум, заслуживает внимания, поскольку имеет непосредственное отношение к пространствам, подпадающим под рассматриваемое в настоящей работе понятие скалярного полипроизведения.
Итак, попытаемся представить себе мир, в котором роль пространства Минковского выполняло бы квадрагиперболическое пространство. В этом мире вместо двух изотропных конусов геометрии Минковского, разделяющих абсолютное прошлое и будущее от области абсолютно удаленных событий, фигурируют четыре изотропных гиперплоскости, в совокупности разделяющих всё квадрагиперболическое пространство на шестнадцать односвязных областей. Не полное, но все же достаточно верное, представление о структуре этих областей дает рис.1,
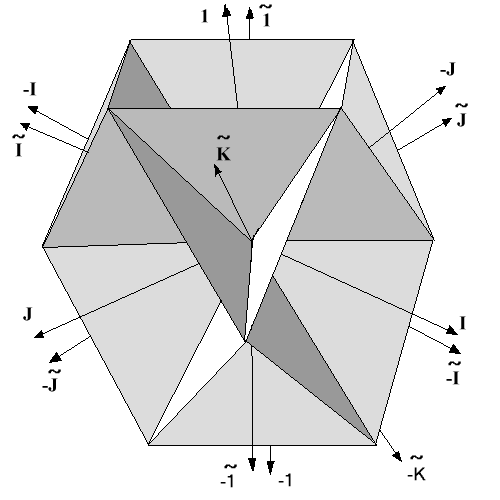
Рис. 1
![]()
![]()
на котором изображено сечение
квадрагиперболического пространства
гиперплоскостью a4=0. На этом рисунке
изображены четырнадцать (семь из них
скрыто плоскостью чертежа) из шестнадцати
односвязных областей, лучи симметрии
которых совпадают с направлениями
векторов: 1, -1, I, -I, J, -J, K (отсутствует),
-K (отсутствует),
![]() ,
а от изотропных гиперплоскостей из-за
подавления одной из координат остались
только плоскости. Связь фигурирующих
на рис.1 единичных векторов с изотропными
векторами выделенного базиса S1,
S2, S3, S4
[10], в котором представлена форма (8)
выражается следующими линейными
комбинациями:
,
а от изотропных гиперплоскостей из-за
подавления одной из координат остались
только плоскости. Связь фигурирующих
на рис.1 единичных векторов с изотропными
векторами выделенного базиса S1,
S2, S3, S4
[10], в котором представлена форма (8)
выражается следующими линейными
комбинациями:
|
A |
B |
|
1=S1+S2+S3+S4; |
-1=-S1-S2-S3-S4; |
|
I=S1-S2+S3-S4; |
-I=-S1+S2-S3+S4; |
|
J=S1+S2-S3-S4; |
-J=-S1-S2+S3+S4; |
|
K=S1-S2-S3+S4; |
-K=-S1+S2+S3-S4; |
|
C |
D |
|
|
|
|
|
|
|
|
- |
|
|
- |
По сути представляющих собой перебор всех возможных комбинаций знаков при суперпозиции изотропных векторов S1, S2, S3, S4. Соответствующие единичные вектора разбиты на четыре группы A, B, C, D. Вектора групп A и B имеют значения полиформ равные плюс единице, а вектора групп C и D – минус единице. У каждого вектора из группы A или C есть противоположно направленный вектор в группе B или D, соответственно.
Внутри каждой из групп, любые два вектора однократно и трёхкратно трансверсальны друг другу, то есть
(1,I,I,I)=(1,1,1,I)=…=(J,J,J,K)=(J,K,K,K)=0.
А любой вектор из группы A и B двукратно трансверсален любому из векторов групп C и D, то есть
(1,1,I,I)= (1,1,![]() ,
,![]() )=…=(J,J,
)=…=(J,J,![]() ,
,![]() )=0.
)=0.
Таким образом, указанные пары векторов иллюстрируют собой два (а, вернее, три) типа ортогональности присущей квадрагиперболическому пространству,- свойство в принципе отсутствующее в билинейных пространствах, а потому несколько экзотическое.
Если внутри одной из шестнадцати односвязных областей (например, в области вектора 1) произвольный луч принять по определению за направление собственного времени некоторой инерциальной системы отсчета, тогда все лучи, лежащие в других областях, окажутся по отношению к нему мнимыми. Все направления данной области - будут действительными и положительными, что позволяет именовать их, как и в пространстве Минковского, времениподобными. Математически это означает, что каждый вектор внутри выделенной области имеет экспоненциальную форму представления [10], а для экспоненциального представления остальных векторов, формально требуется использование эллиптически мнимой единицы i, которой просто не существует в алгебре квадрагиперболических чисел.
Область времениподобных направлений ограничена четырьмя изотропными гранями, которые в совокупности выполняют практически ту же роль, что и световой конус будущего в геометрии Минковского, поэтому сохраним за ним то же название. На первый взгляд может показаться, что изотропные направления, лежащие на границе светового конуса не равноправны, так как они представляют собой четырехгранную пирамиду и, по крайней мере, направления, совпадающие с ребрами, должны отличаться от остальных. Но эта анизотропия кажущаяся и обусловлена издержками способа представления финслерова пространства с помощью евклидовой модели. Аналогичный эффект имеет место, когда на евклидовой плоскости пытаются изобразить особенности псевдоевклидова пространства. Геометры уже давно свыклись с необходимостью при рассмотрении подобных картинок учитывать только общие аффинные свойства и не замечать принципиально различных метрических особенностей изучаемого пространства и пространства изображений. Во всяком случае, если исходить из законов самого квадрагиперболического пространства, а не из того, как оно выглядит на евклидовом чертеже, все изотропные направления абсолютно равноправны. В этом смысле квадрагиперболическое пространство ничуть не более анизотропно, чем псевдоевклидово и даже обладает более высокой степенью симметрии, так как не противопоставляет временные и пространственные направления.
Если, по аналогии с пространством Минковского, с каждым изотропным направлением квадрагиперболического пространства связывать мировые линии сигналов, движущихся с одинаковыми и максимально возможными скоростями, не сложно показать, что величина этой скорости оказывается не зависящей от того, какое из направлений в действительной области принято за ось времени. В переводе на физический язык это утверждение эквивалентно тезису о независимости скорости света, от скорости системы отсчета, и в этом смысле рассматриваемое пространство устроено подобно пространству специальной теории относительности.
C двумя несовпадающими направлениями внутри конуса будущего квадрагиперболического пространства также, как и в пространстве Минковского, можно связывать понятие относительной скорости двух объектов, мировые линии которых сопоставляются этим направлениям. Однако, в нашем случае относительная скорость будет зависеть уже не от одного скалярного параметра (в пространстве Минковского это гиперболический угол), а от трёх, что является следствием квадралинейности принятой финслеровой геометрии. При этом качественная сторона закона сложения скоростей оказывается во многом совпадающей с закономерностями специальной теории относительности: при малых скоростях весьма точно работают законы классической механики, а при высоких - реализуются релятивистские эффекты.
Однако, при всей схожести, квадрагиперболическое пространство все же принципиальным образом отличается от псевдоевклидова. Односвязной области абсолютно удаленных событий пространства Минковского в нашем случае соответствуют четырнадцать обособленных областей, причем каждая из них практически идентична областям внутри конусов абсолютного будущего и прошлого. Если существует мир, в котором реализуется метрика квадрагиперболического пространства, в нем царит весьма строгая симметрия всех характерных направлений.
Другим необычным фактом мира с квадрагиперболической метрикой является относительность его материальных образований (если, конечно, последние в нём вообще возможны). В таком мире должны проявляться минимум два структурных уровня. Первый уровень – исключительно геометрический. На этом уровне бессмысленно говорить о времени, пространстве, материи, энергии и других привычных атрибутах физического мира. Это уровень чистого пространства, наделенного только геометрической структурой, описание которой возможно с помощью тензора кривизны общей теории относительности, с той разницей, что роль метрического тензора в квадрагиперболическом многообразии должен играть несколько иначе устроенный геометрический объект. Кроме того, возможны и другие способы описания искривленных квадрагиперболических многообразий, принципиально непригодных для псевдоримановых пространств, поскольку последние существенно обделены группой конформных отображений.
Второй структурный уровень проявляется только тогда, когда в квадрагиперболическое пространство некоторым образом вводится наблюдатель, то есть, появляется нечто, что выделяет одно из неизотропных направлений, как направление собственного времени. Именно по отношению к наблюдателю, а вернее по отношению к связанному с ним направлению времени, объективно существующая в пространстве и, в общем-то, единая четырёхмерная геометрическая структура, распадается на две качественно отличных сущности – одномерное время и трёхмерное пространство. Именно наблюдатель, связанный изначально присущим ему собственным временем, оказывается “ответственным” за то, в каких образах предстанет перед ним окружающий мир. Если исходная геометрическая структура не является тривиально простой, вполне вероятно ожидать, что её складки, искривления и узлы будут трактоваться нашим наблюдателем, как материальные объекты и поля, погруженные в трёхмерное пространство и вовлечённые в эволюционный процесс. Каким наш гипотетический наблюдатель “увидит” трёхмерный мир, и какими метрическими закономерностями его наделит, в основном зависит от объективных свойств квадрагиперболического пространства. Однако немаловажна и другая часть данного процесса, которая чисто субъективна и зависит от того, каким способом наблюдатель будет пользоваться, что бы идентифицировать окружающие его трёхмерные объекты, а так же, каким образом будет наделять эти объекты характеристикой разделяющих их расстояний.
Удивительной особенностью квадрагиперболического пространства оказывается то обстоятельство, что если наш гипотетический наблюдатель будет измерять расстояния между мировыми линиями объектов, практически параллельных его собственной, с помощью сигналов, скорость которых много меньше предельно возможной, он с необходимостью придет к метрике трёхмерного евклидова пространства! Таким образом, имеется, по крайней мере, один способ совместить геометрию квадрагиперболического пространства с классическими представлениями о евклидовой структуре реального мира.
Если от направления собственного времени одного пробного наблюдателя перейти конгруэнтным преобразованием к другому (то есть, осуществить непрерывное вращение в пространстве-времени), то такой переход эквивалентен изменению скорости системы отсчета, со всеми известными из СТО качественными особенностями. Но если вектор собственного времени пробного наблюдателя перевести внутрь другого изотропного конуса (что возможно сделать только дискретным преобразованием), картина должна поменяться радикальным образом. Оставшаяся неизменной исходная четырёхмерная геометрическая структура, теперь реализуется перед наблюдателем с позиций совершенно иного представления о трёхмерном физическом пространстве, что связано с переходом временной оси в другую односвязную область. Естественно, что при такой фундаментальной метаморфозе должны поменяться представления наблюдателя не только об одном из пространственных и временном направлениях, но и о материальных объектах, наполняющих его “старую” и “новую” действительность. Такой гипотетический наблюдатель оказывается как бы в другой вселенной, хотя обе они просто две стороны одного исходного квадрагиперболического многообразия. Таких “смежных” субъективно различных вселенных в квадрагиперболическом пространстве шестнадцать, по количеству односвязных областей, разделенных изотропными гиперплоскостями. Правда, что бы проникнуть в любую из таких вселенных наш наблюдатель должен разогнаться до скорости света и перейти через неё, что, как и в специальной теории относительности, физически, вряд ли, осуществимо.
Если намеченный выше алгоритм соотнесения реального пространства-времени с квадрагиперболическими многообразиями, хотя бы отчасти имеет право на существование, возникает задача отыскания фундаментальных принципов построения соответствующих многообразий, что бы генерируемые на их основе образы физической реальности соответствовали экспериментально наблюдаемым фактам. Эти принципы, возможно, окажутся связанными с группой конформных отображений, или же, что более вероятно, c их специфическими обобщениями.
Возникающая картина, при всей своей фантастичности, философски и математически вполне оправдана, так как строится не абстрактно, а на фундаменте относительно небольшого количества аксиом, к тому же весьма согласованных друг с другом. И все же здесь, пожалуй, нам пора остановиться, так как имеющихся на сегодня математических и экспериментальных данных пока не достаточно, что бы делать однозначные утверждения.
Конечно, резонно задаться вопросом, а зачем, собственно, искать замену пространству Минковского, да еще столь экзотическую? Можно выдвинуть три основных аргумента: во-первых, постоянные нестыковки в многочисленных попытках найти картину объединения фундаментальных взаимодействий на базе моделей с квадратичной формой метрики наталкивают на мысль посмотреть, не изменится ли ситуация к лучшему, с принятием постулата n-арности метрической формы; во-вторых, некоторые поличисловые пространства, в отличие от пространства Минковского, естественным образом связаны с расширением понятия числа и конформного отображения, являющимися, несомненно, одними из основных категорий естествознания и, наконец, предлагаемые аксиомы полискалярного произведения дают возможность по-новому взглянуть на некоторые известные факты, а, значит, позволяют существенно расширить горизонты исследований.
Список литературы:
1. Гельфант И.М. Лекции по линейной алгебре. М., «Наука», 1966.
2. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. М., «Наука», 1973.
3. Розенфельд Б.А. Многомерные пространства. М., «Наука», 1966.
4. Мальцев А.И. Основы линейной алгебры. М., «ТТЛ», 1956.
5. Лаврентьев М.А., Шабат Б.О. Проблемы гидродинамики и их математические модели. М., «Наука», 1977.
6. Розенфельд Б.А. Неевклидовы пространства. М., «Наука», 1969.
7. Olariu S. Complex Numbers in n Dimensions. ArXiv:CV/0011044.
8. Davenport C.M. Commutative Hypercomplex Mathematics. //[http://home.usit.net/~cmdaven/hyprcplx.htm]
9. Елисеев В.И. Введение в методы теории функций пространственного комплексного переменного. //[http://www.maths.ru]
10. Pavlov D.G. Hypercomplex Numbers, Associated Metric Spaces, and Extension of Relativistic Hyperboloid. ArXiv:gr-qc/0206004.
11. Рунд Х. Дифференциальная геометрия финслеровых пространств. М., «Наука», 1981.
12. Кассандров В.В. Вестник Российского Университета Дружбы Народов., Физика, 1, 1993.
13. Кассандров В.В. Число, время, свет. //[http://www.chronos.msu.ru]
+++
