Глава IV Движение вязкой жидкости при малых числах Рейнольдса
§1. Уравнения движения ньютоновской жидкости при малых числах Рейнольдса
Рассмотрим некоторые приближенные решения уравнений движения для предельного случая, в котором силы трения значительно больше, чем силы инерции.
Для стационарного движения несжимаемой ньютоновской жидкости уравнение Навье-Стокса имеет вид:
р
(4.1)
Инерционный член
имеет
порядок величины
,
где u
– характерная скорость, l
– некоторый
характерный размер. Выражение же
порядка
.
Отношение инерционного члена к вязкому
есть число
Рейнольдса. Поэтому при Re
<< 1 членом
можно пренебречь и уравнение движение
сводится к линейному уравнению:
р
(4.2)
Следует учитывать, что массовые силы (вес) играют роль либо при наличии свободной поверхности или для неоднородной жидкости. При движении однородной жидкости, вместо давления рассматривается разность между действительным давлением и давлением в состоянии покоя (гидростатическим давлением).
Уравнение (4.2) вместе с уравнением неразрывности:
(4.3)
полностью определяет
движение. Граничные условия для системы
уравнений (4.2) и (4.3) такие же как и для
полных уравнений Навье-Стокса, то есть
на твердых поверхностях выполняются
условия прилипания жидкости к стенкам:
,
.
§2. Пространственное движение ньютоновской несжимаемой жидкости между двумя безграничными параллельными плоскостями. Закон Дарси
Рассмотрим
пространственное движение вязкой
несжимаемой жидкости между двумя
безграничными параллельными плоскостями,
расположенными на малом расстоянии 2h
друг от друга, точнее на таком, что Re
=
мало. Между плоскостями могут располагаться
перпендикулярные к плоскостям
цилиндрические препятствия той же
высоты 2h
[3].
Расположим плоскость Оxy в срединной плоскости, а ось Оz направим перпендикулярно к ограничивающим поток плоскостям. Считаем, что движение происходит в плоскостях, параллельных границам потока, тем самым примем, что w = 0. Тогда система уравнений (4.2) и (4.3) примет вид:
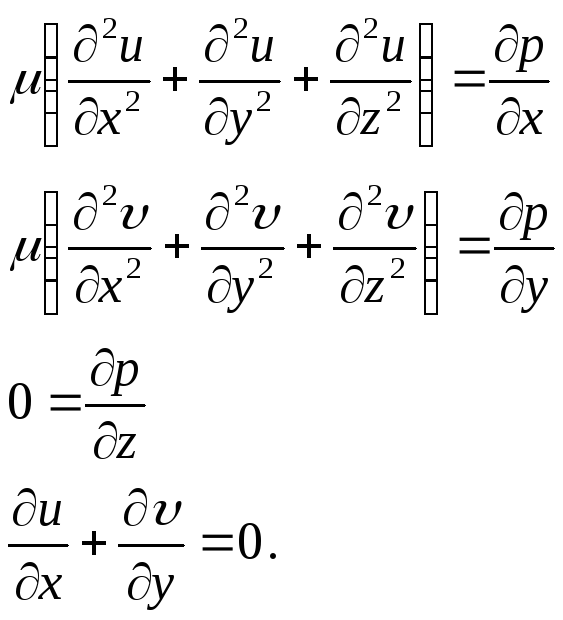(4.4)
Граничные условия запишутся в виде
u
=
= 0 при z
=
. (4.5)
Так как
,
то р = р (х,у).
Возьмем производную по х от обеих частей первого уравнения системы (4.4), по y – от обеих частей второго уравнения той же системы и сложив результаты, для определения р (х,y) получим уравнение Лапласа:
. (4.6)
Пользуясь (4.6), легко простой подстановкой убедиться, что уравнениям (4.4) и граничным условиям (4.5) можно удовлетворить, положив
, 
. (4.7)
Составим средние
по нормали к ограничивающим поток
плоскостям скорости
и
по формулам:
, 
. (4.8)
Из (4.7) найдем максимальные скорости
, 
. (4.9)
Следует иметь в виду, что решения (4.7) теряют свою силу вблизи поверхности, помещенной в поток короткого цилиндрического тела, однако область эта по сравнению с размерами тела невелика, и ее влиянием можно пренебречь, что подтверждается опытами.
Рассмотренному движению близко по механизму движение вязких жидкостей сквозь пористые среды. Закон Дарси, открытый на основании опытов, является обобщением зависимости (4.8) средней скорости от градиента давления. Закон Дарси представляет по существу результат пространственного осреднения движения вязкой жидкости по случайно ориентированным и разнообразным по геометрической форме порам фильтрующей среды. Закон Дарси сходен с законами строго определенных движений той же жидкости при малых Re в тонкой щели между параллельными плоскостями. Для Re << 1 при протекании вязкой жидкости сквозь поры можно пренебречь конвективными ускорениями, вызываемыми кривизной пор и переменностью площади их сечений.
При движении вязких жидкостей сквозь пористые среды со сравнительно большими средними размерами пор линейный закон Дарси уже не работает и должен быть заменен нелинейным законом. Это объясняется влиянием конвективных ускорений в потоке, а затем и переходом к турбулентному режиму фильтрации.