
- •8.1 Вступ до кінематики
- •8.2 Способи опису руху точки
- •8.3. Похідна векторної функції за скалярним аргументом
- •8.4. Швидкість точки
- •8.4.1. Векторний спосіб визначення швидкості. Годограф швидкості
- •8.4.2. Координатний спосіб визначення швидкості
- •8.4.3. Натуральний спосіб визначення швидкості
- •8.5. Прискорення точки
- •8.5.1 Векторний спосіб визначення прискорення
- •8.5.2. Координатний спосіб визначення прискорення
- •8.5.3 Натуральний спосіб визначення прискорення
- •8.5.3.1 Деякі відомості з диференціальної геометрії
- •8.3.2. Розкладання вектора прискорення точки за осями натурального тригранника (нормальна і дотична складові прискорення)
- •8.6. Окремі випадки руху точки при натуральному способі опису руху
- •8.6.1. Рівнозмінний рух точки
- •8.6.2 Прямолінійний рух точки
- •8.7. Методичні вказівки до розв'язання задач
8.2 Способи опису руху точки
Рівняння, що дозволяють визначити положення точки у вибраній системі відліку в будь-який момент часу, називається кінематичними залежностями руху точки.
Ці рівняння мають різний вигляд, залежно від способу визначення руху точки. Для опису криволінійного руху точки можна застосувати один з трьох способів: векторний, координатний та натуральний.
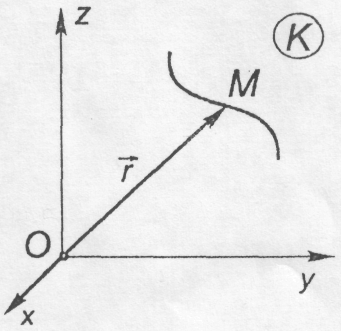
При векторному способі опису руху положення точки у вибраній системі відліку в довільний момент часу визначається радіус-вектором, відносно деякої фіксованої точки О - полюса (рис. 8.1), тобто,
Рис. 8.1![]() (8.1)
(8.1)
Якщо
будувати функцію
![]() в різні моменти часу t1,
t2,
..., tn,
то
геометричним місцем кінців М1,
М2,
..., Мі,
..., Мn,
буде
крива, яка називається траєкторією
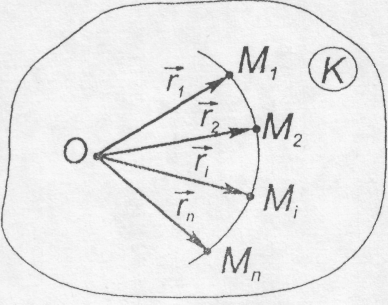
рухомої точки (рис. 8.2). Отже,
співвідношення (1.1) можна розглядати як
рівняння траєкторії точки. Задати
вектор, як функцію часу - це означає
вміти находити його величину і напрям
в будь-який момент часу. Це можна зробити,
якщо вибрана будь-яка система координат.
Тобто, завдання радіуса-вектора як
функції часу, обов'язково передбачає
наявність системи координат, але в той
самий час не зв'язує нас із конкретною
системою координат. Ця обставина дозволяє
широко використовувати завдання
радіуса-вектора як функції часу для
одержання основних
кінематичних характеристик руху.
в різні моменти часу t1,
t2,
..., tn,
то
геометричним місцем кінців М1,
М2,
..., Мі,
..., Мn,
буде
крива, яка називається траєкторією
рухомої точки (рис. 8.2). Отже,
співвідношення (1.1) можна розглядати як
рівняння траєкторії точки. Задати
вектор, як функцію часу - це означає
вміти находити його величину і напрям
в будь-який момент часу. Це можна зробити,
якщо вибрана будь-яка система координат.
Тобто, завдання радіуса-вектора як
функції часу, обов'язково передбачає
наявність системи координат, але в той
самий час не зв'язує нас із конкретною
системою координат. Ця обставина дозволяє
широко використовувати завдання
радіуса-вектора як функції часу для
одержання основних
кінематичних характеристик руху.
 Для
розв'язування конкретних задач, зазвичай,
переходять від векторного способу
до координатного або натурального
способів завдання руху.
Для
розв'язування конкретних задач, зазвичай,
переходять від векторного способу
до координатного або натурального
способів завдання руху.
При координатному способі опису руху положення точки М в довільний момент часу визначається її координатами у вибраній системі координат (декартовій, циліндричній, сферичній тощо), незмінно пов'язаній з тілом відліку.
У прямокутній декартовій системі координат положення точки М визначається координатами x,y,z (рис. 8.3) як функціями часу.
Рис. 8.2![]() (8.2)
(8.2)
Співвідношення (8.2) називаються кінематичними рівняннями руху точки у координатній декартовій формі, їх можна розглядати як рівняння траєкторії точки у параметричній формі (параметром є час t).
Зв'язок між векторним та координатним декартовим способами опису руху точки задається співвідношенням:

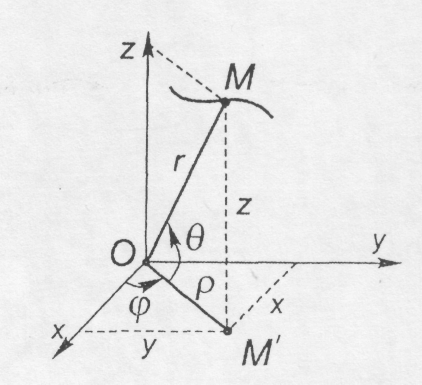
Рис. 8.3 Рис. 8.4
![]() (8.3)
(8.3)
де
![]() - орти (одиничні вектори) системи координат
Oxyz
(рис.
8.3).
- орти (одиничні вектори) системи координат
Oxyz
(рис.
8.3).
У сферичній системі координат, положення точки визначається полярним радіусом r , полярним кутом φ між віссю Ох і напрямом ОМ’ (М’ - проекція точки М на площину Оху , кутом θ між ОМ' і ОМ (рис. 8.4). В процесі руху точки величини r,φ,θ змінюються - вони є функціями часу:
![]() (8.4)
(8.4)
Співвідношення (8.4) називають кінематичними рівняннями руху точки у координатній сферичній формі. Зв'язок між координатним декартовим і координатним сферичним способами опису руху точки задається співвідношеннями:
![]() (8.5)
(8.5)
У циліндричній системі координат (рис. 8.4) положення точки визначається радіусом р , кутом φ між віссю Ох та ОМ' (азимутом), координатою z = MM'. В процесі руху ці величини змінюються як функції часу:
![]() (8.6)
(8.6)
Співвідношення (8.6) називають кінематичними рівняннями руху точки у координатній циліндричній формі.
Зв'язок між координатним декартовим і координатним циліндричним способами опису руху точки такий:
![]() (8.7)
(8.7)
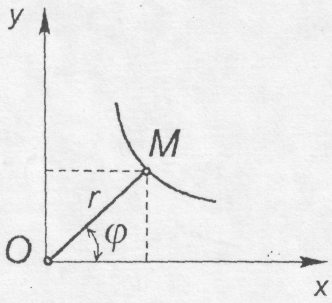 При
дослідженні руху точки на площині
використовується також полярна
система координат (рис. 8.5). Полярними
координатами точки є радіус r
і
кут φ
є процесі
руху точки вони є
При
дослідженні руху точки на площині
використовується також полярна
система координат (рис. 8.5). Полярними
координатами точки є радіус r
і
кут φ
є процесі
руху точки вони є
функціями часу:
![]() (8.8)
(8.8)
Співвідношення (8.8) називається кінематичними рівняннями руху точки у координатній полярній формі.
Рис. 8.5
![]() (8.9)
(8.9)
Рівняння руху точки (8.2) є одночасно і рівняннями траєкторії точки в параметричній формі, де роль параметра відіграє час t. Для того, щоб одержати рівняння траєкторії у координатній формі, необхідно з рівнянь руху виключити час t.
Нехай, наприклад, рух точки в площині ху описаний рівняннями:
![]()
де а,b,с - постійні величини.
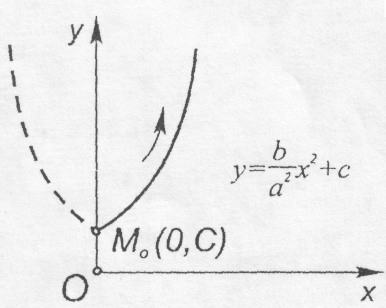 З
першого рівняння визначаємо
З
першого рівняння визначаємо
![]() і
підставляємо його в друге рівняння
і
підставляємо його в друге рівняння
 .
Це рівняння
параболи.
Однак траєкторією буде не вся парабола,
а тільки її права гілка (при t
= 0;
х
= 0;
у
= с),
оскільки час
додатний
і безперервно зростає (рис. 8.6). Такий
метод виключення часу не єдиний. Існують
й інші способи. Наприклад, рух точки
описаний рівняннями:
.
Це рівняння
параболи.
Однак траєкторією буде не вся парабола,
а тільки її права гілка (при t
= 0;
х
= 0;
у
= с),
оскільки час
додатний
і безперервно зростає (рис. 8.6). Такий
метод виключення часу не єдиний. Існують
й інші способи. Наприклад, рух точки
описаний рівняннями:
![]()
де а,b,ω - постійні величини.
Рис. 8.6
![]()
Зведемо до квадрата ліву і праву частини рівнянь і складемо:

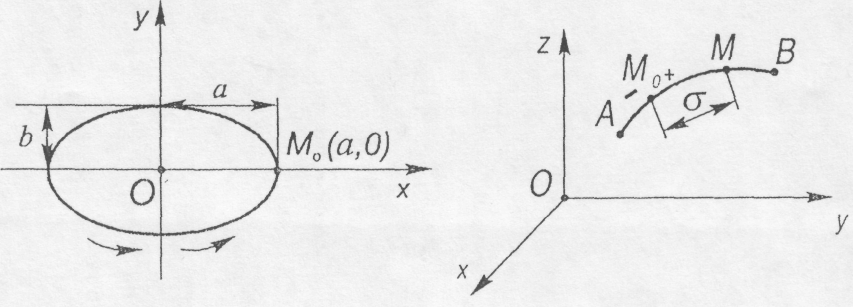
Рис. 8.7 Рис. 8.8
Це рівняння еліпса з напівосями а і b (рис. 8.7).
Натуральний спосіб опису руху точки застосовується тоді, коли траєкторія точки заздалегідь відома.
Положення точки у вибраній системі відліку визначають такі елементи (рис. 8.8):
а) просторова крива АВ (траєкторія точки).
б) початок відліку О дугової координати σ.
в) додатний напрям відліку дугової координати;
г) дугова координата σ на кривій.
В процесі руху точки М дугова координата σ змінюється за часом:
![]() (8.10)
(8.10)
Співвідношення (8.10) називається кінематичним рівнянням руху точки у натуральній формі.
Не
можна змішувати кінематичні рівняння
з рівнянням траєкторії. Крива,
побудована на площині (σ, t)
та
виражає залежність
![]() називається
графіком руху. Якщо рух точки проходить
в сторону зростання дуги σ, то диференціал
дуги
називається
графіком руху. Якщо рух точки проходить
в сторону зростання дуги σ, то диференціал
дуги
![]() буде
додатним,
якщо рух проходить в бік зменшення дуги,
то dσ
буде
від'ємним.
Відзначимо, що шлях S,
який
проходить точка, весь час буде зростати
і, отже, додатний, тобто,
буде
додатним,
якщо рух проходить в бік зменшення дуги,
то dσ
буде
від'ємним.
Відзначимо, що шлях S,
який
проходить точка, весь час буде зростати
і, отже, додатний, тобто,
![]()
Встановимо зв'язок між координатами, декартовим і натуральним способами опису руху точки.
Нехай
рух точки описаний рівняннями (8.2).
Виключаючи з цих рівнянь час t.
одержимо
рівняння траєкторії. Знайдемо тепер
закон руху
![]() .
.
З курсу диференціальної геометрії відомо, що елемент дуги траєкторії dσ визначається виразом:
![]() (8.11)
(8.11)
де dx,dy,dz - диференціали координат точки.
![]()
тоді формулу (1.12) можна записати у вигляді:
![]() (8.11а)
(8.11а)
Інтегруючи цей вираз в інтервалі від t = О (початок руху) до будь-якого моменту t, одержимо закон руху:
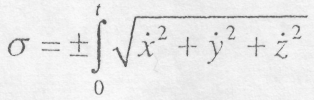 (8.12)
(8.12)
Знак „+" перед інтегралом слід вибирати в тому випадку, коли рух проходить в бік додатного відліку дугової координати, та „-" при русі точки в бік від'ємного відліку дугової координати.
