8.3. Похідна векторної функції за скалярним аргументом

При розгляданні задач кінематики і динаміки, ми будемо зу­стрічатись з необхідністю обчислення похідної векторів, які мають різний фізичний зміст і є функціями різних скалярних аргументів (ча­су, дуги і ін.). В цьому розділі визначимо поняття похідної від вектора за скалярним аргументом, тобто не надаючи конкретного фізичного значення вектору і аргументу. Спочатку введемо поняття годографа вектора.

Крива, яка накреслюється кінцем будь-якої вектора, при непере­рвній зміні скалярного аргументу, коли початок вектора фіксований у деякій точці О, називається годографом векторної функції.

Як позначено на рис. 8.2, годографом радіуса-вектора визна­чаючого положення точки є траєкторія точки.

Припустимо, що вектор - неперервна функція скалярного аргументу u , тобто

При зміні аргументу u буде змінюватись його величина і на­прямок. Кінець вектора , при зміні аргументу u , описує деяку криву - годограф вектора (рис. 8.9). Нехай u - деяке фіксоване значення аргументу, a ∆u >0 означає приріст аргументу u . Тоді, при ар­гументі u + ∆u вектор буде мати іншу величину й інший напря­мок, ніж при значенні аргументу, рівному u .

Геометрична різниця

називається приростом вектора

Границя відношення

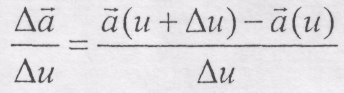
при ∆u → 0, якщо вона існує, називається похідною вектора за скалярним аргументом, а саме:

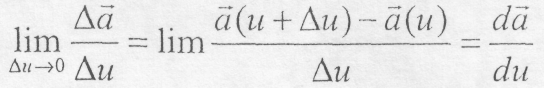(8.13)

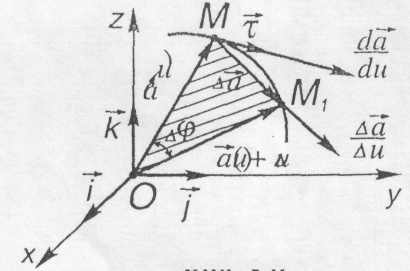
Рис. 8.9

На годографі (рис. 8.9) вектор спрямований по хорді, тобто по січній MM₁, граничне положення якої при ∆u → 0 (точка прямує до точки М) збігається з дотичною до годографа ве­ктора у точці М.

Вектор характеризує швидкість зміни вектора при зміні його аргументу і спрямований по дотичній до годографа, яка проведена у бік зростання значення скалярного аргументу. Якщо век­тор виразити через його проекції а_x,а_y,а_z, на нерухомі осі Ox,Oy,Oz , тобто , то враховуючи, що орти є сталими величинами, дістаємо

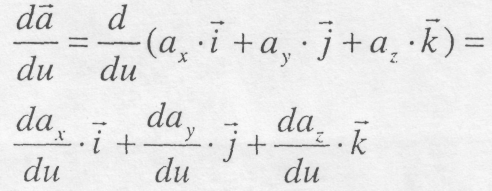^(8.14)

Отже, похідна вектора за скалярним аргументом являє собою вектор, проекції якого на нерухомі осі дорівнюють похідним за тим самим аргументом від проекцій диференційованого вектора.

Модуль похідної визначається з рівності

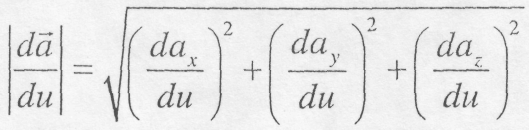^(8.5)

Подамо без доведення властивості похідної вектора за скаляр­ним аргументом:

1. Похідна від постійного за величиною і напрямом вектора дорівнює нулю.

2. Похідна від суми векторів дорівнює сумі похідних, тобто,

^(8.16)

3. Похідні від скалярного і векторного добутків векторів від­повідно визначаються виразами:

^(8.17)

Перейдемо тепер до визначення поняття швидкості руху точки і методу її знаходження.

8.4. Швидкість точки

8.4.1. Векторний спосіб визначення швидкості. Годограф швидкості

Швидкістю точки називається кінематична міра руху точки, що дорівнює похідній за часом від радіуса-вектора цієї точки у даній системі відліку, тобто.

^(8.18)

Ця формула відповідає визначенню швидкості при векторно­му способі опису руху точки. Згідно з поняттям похідної векторної функції за скалярним аргументом, вектор швидкості визначає швид­кість зміни просторового положення точки за часом. Він спрямований по дотичній до годографа вектора у бік зростання аргументу φ (рис. 8.10). тобто по дотичній до траєкторії точки М у бік її руху. За одиницю швидкості в СІ прийнято метр за секунду (м/с). У загальному випадку руху точки швидкість змінюється з часом. Кожному моменту часу відповідає певний вектор швидкості, спрямований по дотичній до траєкторії.

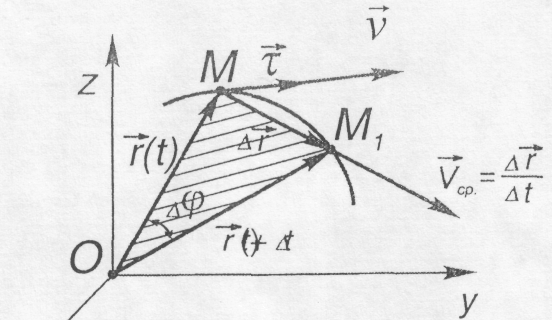
Рис. 8.10

Рис. 8.11

Розглянемо вектори швидкостей (рис. 8.11, а) руху точки М по траєкторії. Виберемо довільну нерухому точку О’ (рис. 8.11) та перенесемо всі вектори швидкості паралельно так, щоб їхні початки збігалися з точкою О’ . Оскільки векторзмінюється за часом, то кінці перенесених векторів утворюють неперервну криву, яка називається годографом вектора швидкості.