
- •I. Материалы ко второму этапу экзамена.
- •Тема №1:«дифференциальное и интегральное исчисления»
- •1. Если производные двух функций тождественно равны, то сами функции
- •26. Если f(X) является одной из первообразных для данной функции f(X), то самое общее выражение, для первообразной имеет вид
- •3. Уравнение, в которое неизвестная функция входит под знаком производной или дифференциала, классифицируется как
- •5. Дифференциальное уравнение относится к
- •6. Особым решением обыкновенного дифференциального уравнения первого порядка является ….
- •7. Общим решением дифференциального уравнения будет
- •Тема 3. «теория вероятностей и мат.Статистика»
- •II. Материалы к собеседованию. Производные и дифференциалы.
- •Интегралы. Неопределённые интегралы.
- •Определённые интегралы.
- •Дифференциальные уравнения.
- •Теория вероятностей и математическая статистика.
- •13. Задана функция плотности случайной величины, распределенной по нормальному закону:
- •15. Случайная величина принимает значения: -0,10; 0,00; 0,10; 0,30; с равными вероятностями. Найдите математическое ожидание и дисперсию.
- •20. Задана функция плотности случайной величины, распределенной по нормальному закону:
- •61. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берут на пробу 2 дм3 воздуха. Найдите вероятность того, что в пробе будет обнаружен хотя бы один микроб.
- •Ответы, указания, решения. Тестовые задания. Тема №1: «Дифференциальное и интегральное исчисления»
- •Тема №3. «Теория вероятностей и мат.Статистика»
- •Производные и дифференциалы.
- •Частные производные. Применение дифференциального исчисления в теории ошибок измерений.
- •Скалярное поле. Производные по направлению. Градиент.
- •Интегралы. Неопределённые интегралы.
- •Определённые интегралы.
- •Дифференциальные уравнения.
- •Теория вероятностей и математическая статистика.
- •Справочные материалы
- •Оглавление
Частные производные. Применение дифференциального исчисления в теории ошибок измерений.
1.D
=
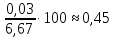 .
.
2. Относительная
погрешность вычисленной площади
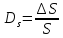 ,
а её приближённое значение мы получим,
заменив в этом равенстве ∆S на dS. В таком
случае
,
а её приближённое значение мы получим,
заменив в этом равенстве ∆S на dS. В таком
случае
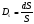 .
Но площадь круга
.
Но площадь круга
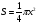 (x-диаметр),
а поэтому
(x-диаметр),
а поэтому
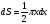 .
Таким образом
.
Таким образом
 .
(Иначе:
.
(Иначе:
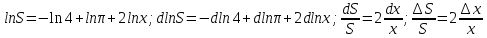 ).По
условию x
= 6,7 см; dx = 0,03 см, а потому
).По
условию x
= 6,7 см; dx = 0,03 см, а потому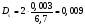 ,
а умножая эту величину на 100, получим
погрешность в процентах, которая равна
(0,009 · 100)% = 0,9%.
,
а умножая эту величину на 100, получим
погрешность в процентах, которая равна
(0,009 · 100)% = 0,9%.
3.Объём
шара вычисляется по формуле
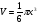 ,
где x - диаметр шара.
Приближённо погрешность ∆V вычисленного
объёма (приращение объёма как функции
диаметра) равна
,
где x - диаметр шара.
Приближённо погрешность ∆V вычисленного
объёма (приращение объёма как функции
диаметра) равна
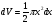 .
Относительная погрешность
.
Относительная погрешность
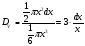 .
Но относительна погрешность измерения
диаметра
.
Но относительна погрешность измерения
диаметра
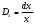 ,
а поэтому
,
а поэтому
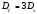 ,
что и требовалось доказать.
,
что и требовалось доказать.
4.DR = 0,66%.
5.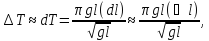 поэтому
относительная погрешность DT
=
поэтому
относительная погрешность DT
=
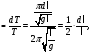 а так как относительная погрешность
измерения длины маятника Dl≈
а так как относительная погрешность
измерения длины маятника Dl≈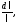 то DT
то DT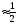 Dl.
Dl.
6.Задача
состоит в определении приращения периода
как функции приращения длины маятника.
Вспомнив, что дифференциал функции
является главной частью приращения
функции, легко получить ответ, найдя
дифференциал периода по переменной -
длине маятника.
 ) =
) =
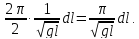 Перейдя к конечным приращениям получим
приближённую формулу:
Перейдя к конечным приращениям получим
приближённую формулу: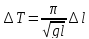 .
Далее:
.
Далее:
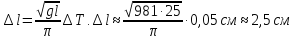 .
Длину маятника следует увеличить на
2,5 см.
.
Длину маятника следует увеличить на
2,5 см.
7.Условие
задачи позволяет считать gфункцией
только длины.

8.Dg
= 2DT;
9.
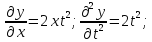 10.
10. 11.
11. ;12.
;12.
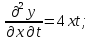
13.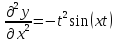 ;14.
;14.
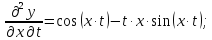 15.
15.
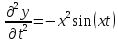 ;
16.
;
16.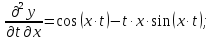 17.
17.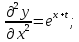 18.
18.
19. «Градиент» скорости и скорость сдвига.
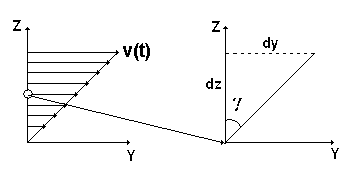
«Градиент» скорости
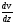 ,
входящий в формулу закона Ньютона для
вязкой жидкости
,
входящий в формулу закона Ньютона для
вязкой жидкости
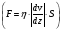 ,
как это видно из рисунка, представляет
собой, с математической точки зрения,
смешанную производную от координаты y
по аргументам zиt.
Обоснованно предположив независимость
аргументов и непрерывность частных
производных по этим аргументам получим:
,
как это видно из рисунка, представляет
собой, с математической точки зрения,
смешанную производную от координаты y
по аргументам zиt.
Обоснованно предположив независимость
аргументов и непрерывность частных
производных по этим аргументам получим:
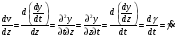
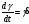 в физике называют скоростью деформации
сдвига (скоростью сдвига) и эта величина
измеряется
в физике называют скоростью деформации
сдвига (скоростью сдвига) и эта величина
измеряется
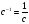 или обратными секундами. Иначе говоря,
скорость деформации при простом сдвиге
или обратными секундами. Иначе говоря,
скорость деформации при простом сдвиге
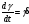 равна градиенту скорости течения
равна градиенту скорости течения
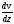 .
.
Скалярное поле. Производные по направлению. Градиент.
1.Полагая u =1, 2, 3, 4, 5, получим уравнения соответствующих линий уровня:
x + y = 1; x + y = 2; x + y = 3; x + y = 4; x + y = 5.
Построив эти линии в прямоугольной системе координат x0y, получим прямые, параллельные биссектрисе 2 – го и 4 - го координатных углов.
2.Написав уравнения линий уровня: x2 +y2 =1, x2 +y2 =2, x2 +y2 =3, x2 +y2 =4, x2 +y2 =5 и построив их в плоскости x0y, получим концентрические окружности с центром в начале координат.
3.Линии уровня 2y = x2, y = x2, 2y = 3x2, y = 2x2, 2y = 5x2представляют параболы, симметричные оси 0y с общей вершиной в начале координат.
4.Находим частные производные функции u и вычисляем их значения в точке А:
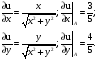
Подставляя в
формулу:
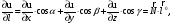 найдём производную функции uв
точке A по любому направлению
найдём производную функции uв
точке A по любому направлению
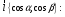
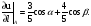
Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииu по заданному направлению.
Для биссектрисы
первого координатного угла: α = β = 450,
cosα = cos
β =
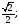
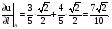
5.Находим частные производные функции u и вычисляем их значения в точке А:
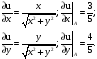
Подставляя в
формулу
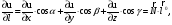 найдём производную функции uв
точке A по любому направлению
найдём производную функции uв
точке A по любому направлению
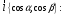
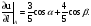
Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииu по заданному направлению.
Для вектора
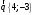 :
, cosα =
:
, cosα =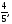 cos
β =
cos
β =
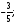
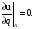
6.Находим частные производные функции u и вычисляем их значения в точке А:
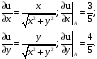
Подставляя в
формулу:
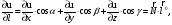 найдём производную функции uв
точке A по любому направлению
найдём производную функции uв
точке A по любому направлению

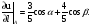
Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииu по заданному направлению.
Для вектора
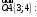 :
, cosα =
:
, cosα =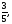 cos
β =
cos
β =
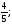
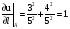
7.Наибольшая по абсолютной величине скорость изменения (возрастания или убывания) функции u (M) при переходе точки Mв точку P численно равна модулю градиента функции в точке P. При этом функция,будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка M при переходе через точку P двигаться по направлению градиента функции в точке Pили по прямо противоположному направлению.
Руководствуясь
этими положениями, находим частные
производные функции u и
по формуле
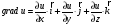 ─
её градиент в любой точке:
─
её градиент в любой точке:
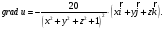 Далее находим:
Далее находим:
1)
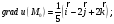
2) его модуль,
численно равный искомой наибольшей
скорости возрастания функции u
(M)при переходе М через
М0, будет
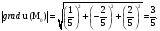
8.Наибольшая по абсолютной величине скорость изменения (возрастания или убывания) функции u (M) при переходе точки Mв точку P численно равна модулю градиента функции в точке P. При этом функция, будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка M при переходе через точку P двигаться по направлению градиента функции в точке Pили по прямо противоположному направлению.
Руководствуясь
этими положениями, находим частные
производные функции u и
по формуле
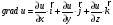 ─её
градиент в любой точке:
─её
градиент в любой точке:
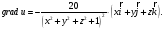 Далее находим:
Далее находим:
1)
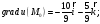
2) искомый вектор, имеющий прямо противоположное направление, будет
─
Чтобы функция u
(M) убывала с наибольшей
скоростью, при переходе через точку
M1точка M
должна двигаться в направлении ─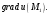
9.Чтобы
в некоторой точке P
производная функции по любому направлению
была равна нулю, необходимо и достаточно,
чтобы в этой точке все частные производные
первого порядка функции одновременно
обращались в нуль. [Согласно формуле:
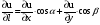 .]
.]
Поэтому, найдя частные производные:
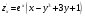 и
и
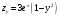 и решая систему уравнений
и решая систему уравнений
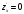 и
и
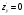 ,
получим две точки: (-3, 1) и (1, -1), в которых
функция стационарна.
,
получим две точки: (-3, 1) и (1, -1), в которых
функция стационарна.
10.Поверхностями уровня данного поля являются концентрические сферы с центром в начале координат: x2 + y2 +z2 = С.
11.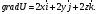
12.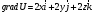 Найдём единичный вектор
Найдём единичный вектор
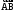 :
:

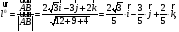
а затем производную
скалярного поля U по
направлению вектора
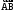 в точке А:
в точке А:
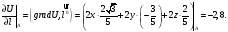
Так как
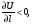 то данное скалярное поле убывает в
направлении вектора
то данное скалярное поле убывает в
направлении вектора
 .
.
13. 1). Воспользуемся определением градиента скалярной функции:
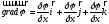
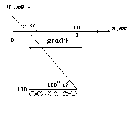
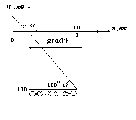
2).
Направим ось x
поперёк мембраны снаружи внутрь. Учтём,
что вданном случае, потенциал – скалярная
функция только одной координаты х,
тогда: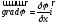 .
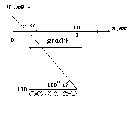
3). Изобразим график зависимости потенциала
от координаты x.
.
3). Изобразим график зависимости потенциала
от координаты x.
4). По графику можно определить tgα. Видно, что он отрицательный и по определению равен производной потенциала по координате x. Вычислим производную.

5).
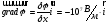 ,
т.е. вектор градиент потенциала направлен
наружу клетки и по модулю равен
,
т.е. вектор градиент потенциала направлен
наружу клетки и по модулю равен
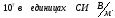
14.По
известному выражению для потенциала
поля точечного электростатического
диполя
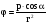 найдём модуль напряжённости поля. При
этом учтём, что особым выделенным
направлением в данном случае окажется
направление, совпадающее с направлением
дипольного момента P.
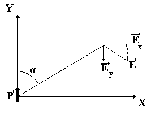
Если расположить диполь в пространстве
так, что он находится в начале координат
и направлен вдоль оси Y,
то картина силовых линий поля диполя
окажется одинаковой для любой плоскости,
проходящей через вектор дипольного
момента. φ и Ε
симметричны относительно оси Y.
найдём модуль напряжённости поля. При
этом учтём, что особым выделенным
направлением в данном случае окажется
направление, совпадающее с направлением
дипольного момента P.
Если расположить диполь в пространстве
так, что он находится в начале координат
и направлен вдоль оси Y,
то картина силовых линий поля диполя
окажется одинаковой для любой плоскости,
проходящей через вектор дипольного
момента. φ и Ε
симметричны относительно оси Y.
Воспользуемся
связью напряжённости электростатического
поля с его потенциалом
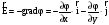 и найдём проекции вектора напряжённости
и найдём проекции вектора напряжённости
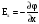 и
и
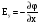 .
После чего модуль вектора напряженности
получится как:
.
После чего модуль вектора напряженности
получится как: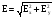 .
.
На плоскости XY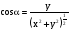 ,
,
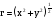 и
и
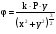 .
.
Для проекции
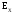 получим
получим
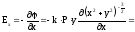

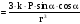 .
.
Для проекции
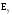 получим:
получим:
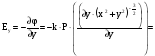
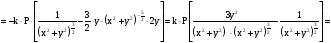
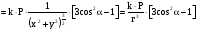 .
.
Итак: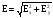 ,иначе
,иначе
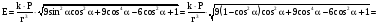
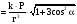 .
.
