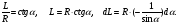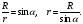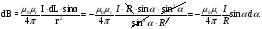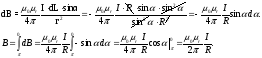Интегралы. Неопределённые интегралы.
1.
1). Применим формулу интегрирования
по частям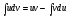
.
2). Положим u = x,
найдём dv: dv
= cosxdx. 3). Найдём du:
du = dx. 4).
Найдём v: v
=
.
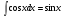5). Получим ответ:
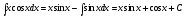
2.
3.
4.
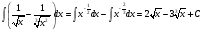
5.
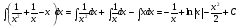
6.
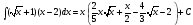
7.
.
8.
.
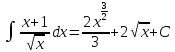9.
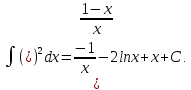
10.
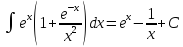
11.
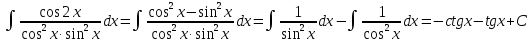
12.
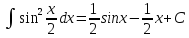
13.
.
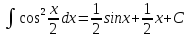14.
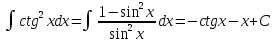
15.
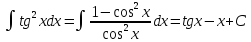
16.
.
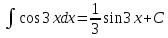17.
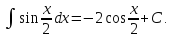
18.
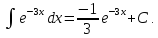
19.
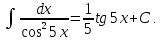
20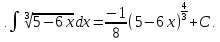
21.
+
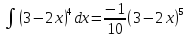C.
22.
+
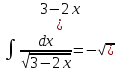C
23.
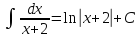
24.
25.
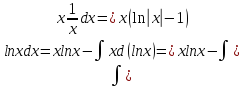+C.
26.
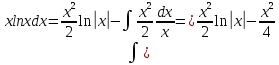+C.
27.
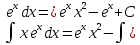
28.Интеграл
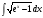берётся
методом замены переменной.
Обозначим
,
тогда:
,
,
,
,
.
=
=
=
=
=
=
=
=
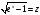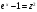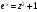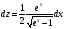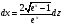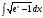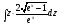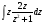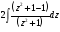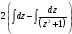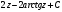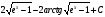
Определённые интегралы.
1.
1).
Получите первообразную от функции
.
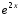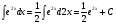
2). Примените формулу
Ньютона-Лейбница.
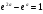
3). Приняв
за переменную z, квадратное
уравнение. . z2 – z
= 2
4). Решите полученное квадратное уравнение.
z1,2
=
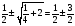; z = 2
5). Подставьте
.
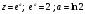2.1). Изобразим схематически капилляр и выделим вблизи оси капилляра малый цилиндр радиуса rc площадью основания S = πr2:
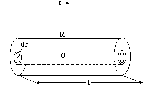
2). Запишем выражение
для Nт, формализовав
его в виде интеграла по всему объёму
трубки - капилляра:
.
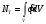где dV -объём цилиндрического
слоя, полученного при изменении радиуса
малого приосевого цилиндра радиуса r
и длины l, т.е. dV
= l·dS и dS =
d(πr2)
= π2rdr
3).
Запишем выражение для тепловой мощности,
учитывая связь удельной тепловой
мощности с напряжением сдвига и скоростью
сдвига:
.
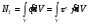4). Учтём зависимости напряжения сдвига и скорости сдвига от радиуса - расстояния от оси трубки r. Запишем выражение для тепловой мощности в виде интеграла по r.
Ответ:
.
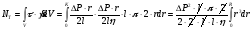5). Возьмём интеграл,
сформируем окончательный ответ:
.
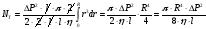И окончательно:
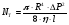
3.
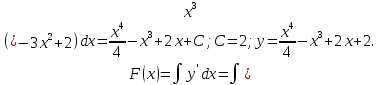
4.Для решения задачи мысленно разобьём протекающую через капилляр за единицу времени жидкость на концентрические трубчатые слои настолько тонкие, чтобы можно было считать линейные скорости частиц жидкости в такой цилиндрической оболочке одинаковыми.
Вклад (dQ),
который делает объём такой цилиндрической
оболочки в расход, легко подсчитать.
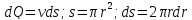
Расход найдём,
если проинтегрируем по всему капилляру:
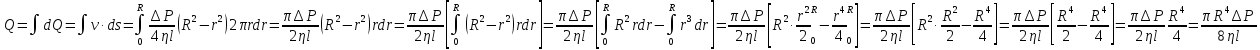
5.
Схематически изобразим изотерму
в координатах p, V,
воспользовавшись известным из школьного
курса физики законом Бойля – Мариотта.
Покажем на графике значения давления
и объёма в начале и в конце процесса
(P1,V1
и P2,V2).
Покажем в виде заштрихованного
прямоугольника элементарную работу
.
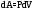Идентифицируем
работу в процессе как площадь криволинейной
трапеции на графике процесса. Подсчитаем
площадь криволинейной трапеции как
определённый интеграл :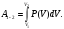
Используя
закон Бойля-Мариотта получим функциональную
зависимость давления от объёма: P·V
= P1·V1,
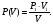
Подставим, полученную
функцию, в определённый интеграл:
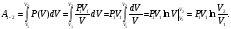
Уравнение
Менделеева-Клапейрона запишем в виде
выражения:
.
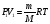Подставим в, полученное выражение и
получим:
Используем закон Бойля-Мариотта, поучим связь между давлениями и объёмами для двух состояний газа. Сформулируем окончательный ответ:
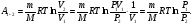
6.Схематически
изобразим изотерму в координатах p,
V, воспользовавшись
известным из школьного курса физики
законом Бойля – Мариотта. Покажем на
графике значения давления и объёма в
начале и в конце процесса (P1,V1
и P2,V2).
Покажем в виде заштрихованного
прямоугольника элементарную работу
.
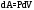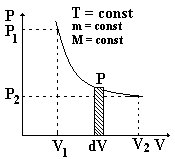
Идентифицируем
работу в процессе как площадь криволинейной
трапеции на графике процесса. Подсчитаем
площадь криволинейной трапеции как
определённый интеграл:
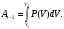Используя
закон Бойля-Мариотта : P·V
= P1·V1,
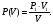
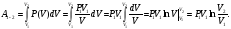
Уравнение
Менделеева-Клапейрона запишем в виде
выражения:
.
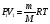И получим:
7.Интеграл
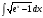берётся
методом замены переменной.
Обозначим
,
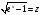тогда:
,
,
,
,
.
=
=
=
=
=
=
=
=
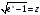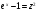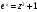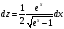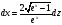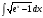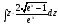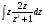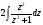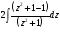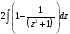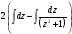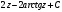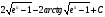
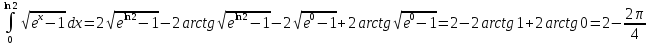.8.
Для определения индукции магнитного
поля вблизи провода воспользуемся
законом Био - Савара – Лапласа:
( )
.
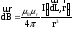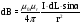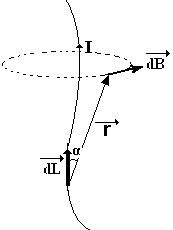
Для прямого бесконечно длинного провода с током применение закона даёт:
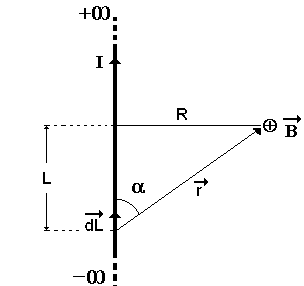
Переменные r,
L, α выразим
через одну (α).
