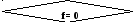- •Тема 1. Решение систем линейных алгебраических уравнений прямыми методами.
- •Вычислим значения определителей всех пяти матриц (c использованием функции мопред среды excel). Получим
- •Система не имеет решений
- •Вывод значений решения
- •Система не имеет решений
- •Вывод значений корней
- •Тема 2. Решение систем линейных алгебраических уравнений итерационными методами.
- •Вычислим норму матрицы d. Получим
- •Вычислим ее норму. Получим
- •Так как норма матрицы d оказалась меньшей единицы, преобразованная таким образом система пригодна для решения методом простой итерации.
- •Тема 3. Обращение квадратных матриц,
- •Система не имеет решений
- •Вывод значений решения
Вычислим значения определителей всех пяти матриц (c использованием функции мопред среды excel). Получим
![]()
Так как определитель матрицы A не равен нулю - система имеет единственное решение. Тогда определим по формуле (2.4). Получим
![]()
![]()
Метод Гаусса. Решение СЛАУ этим методом предполагает посредством эквивалентных преобразований приведение расширенной матрицы системы (расширенная матрица системы - это матрица размером в n строк и n+1 столбцов, включающая в себя исходную матрицу A c присоединенным к ней столбцом, содержащим вектор B) к треугольному виду (так, чтобы ниже ее главной диагонали находились только нулевые элементы). Тогда начиная с последней строки и двигаясь вверх можно последовательно определить значения всех компонент решения.
Эквивалентными преобразованиями системы линейный уравнений называются такие ее преобразования, которые не изменяют ее решения. К их числу относятся :
-
перестановка местами двух любых уравнений системы
-
умножение (или деление) какого-либо уравнения системы на число, не равное нулю
-
прибавление к одному уравнению системы другого ее уравнения, умноженного (или разделенного) на некоторое, не равное нулю, число.
Начало преобразований расширенной матрицы системы к необходимому виду заключается в просмотре значений коэффициентов при x1 и выборе строки, в которой он имеет максимальное по абсолютной величине значение (это необходимо для уменьшения величины вычислительной ошибки при последующих вычислениях). Эту строку расширенной матрицы необходимо поменять местами с первой ее строкой. После этого все элементы этой новой первой строки (в том числе и в последнем ее столбце) необходимо разделить на этот коэффициент. После этого вновь полученный коэффициент a11 станет равным единице. Дальше от каждой из оставшихся строк матрицы необходимо вычесть ее первую строку, умноженную на значение коэффициента при x1 в этой строке (т.е. на величину ai1, где i=2, 3, …n). После этого во всех строках, начиная со второй коэффициент при - все коэффициенты aii =1 (i=1, 2, …, n) будет равным нулю. Поскольку мы выполняли только эквивалентные преобразования - решение вновь полученной СЛАУ не будет отличаться от исходной системы.
Дальше, оставляя неизменной первую строку матрицы, проделаем все вышеописанные действия с остальными строками матрицы и, в результате, вновь полученный коэффициент a22 станет равным единице, а все коэффициенты ai2 (i=3, 4, …, n) станут равными нулю. Продолжая аналогичные действия, мы в конечном итоге приведем нашу матрицу к виду, в котором
- все коэффициенты aii = 1 (i=1, 2, …, n),
- все коэффициенты aij = 0 (i=2, 3, …, n, j<i).
После этого, обратным ходом, можно найти значения всех xi, составляющих решение исходной системы.
Если на каком-то шаге при поиске наибольшего по абсолютной величине коэффициента при xj мы не сможем найти не равного нулю коэффициента - это будет значить, что исходная система не имеет единственного решения. В этом случае процесс решения необходимо прекратить.
Достаточно подробный алгоритм решения СЛАУ методом Гаусса приведен на рис. .2.1 и рис. 2.1а.
Пример 2. Найти методом Гаусса решение той же СЛАУ, которую мы уже решали методом Крамера. Составим сначала ее расширенную матрицу. Получим
A*
=
 .
.
Сначала переставим местами первую и третью строки этой матрицы (так как в ее первом столбце находится наибольший по абсолютной величине элемент), а затем разделим все элементы этой новой первой строки на значение 3. Получим
A*
=
 .
.


Ввод
значения размерности N
и N
строк коэффициентов расширенной
матрицы.

f
:=
0 ; i
:= 10; f
– флаг
вырожденности матрицы




Поиск
строки k,
в которой
aki
= max
aji
для j
i.
да
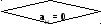
да


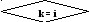


Перестановки
местами элементов строк k
и
i
расшир.
матрицы
Деление
всех элементов строки i
на значение
элемента a
ii

k
:= i + 1
нет






От
всех элементов строки k
вычесть
соответствующие элементы
строки i,
умноженные на значение aki f
:=1

k
:= k + 1 Прямой
ход.


i
:= i + 1 да



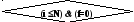

нет да