Система не имеет решений

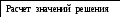
Вывод значений решения

Рис. 2.1. Алгоритм решения систем линейных алгебраических уравнений методом Гаусса

i := N

x_i := a _{i N+1}

j := i + 1

да

x_i := x_i – a_ij x_j

j := j + 1

i := i - 1

нет

Рис. 2.1а. Макроблок “Расчет значений решения”.

Обратный ход.

Дальше проведем вычитание из каждой строки матрицы (кроме первой) элементов первой строки, умноженных на коэффициент в первом столбце этой строки. Получим

A* =

Дальше переставим местами вторую и третью строки этой матрицы, разделим вторую строку переставленной матрицы на 2.3333 и, аналогично вышеописанному, обнулим коэффициенты во втором столбце третьей и четвертой строк матрицы. Получим

A* = .

После выполнения подобных действий над третьей и четвертой строками матрицы получим

A* = .

Разделив теперь четвертую строку на -5.3076, закончим проведение расширенной матрицы системы к диагональному виду. Получим

A* = .

Из последней строки сразу получим x₄=0.7536. Поднимаясь теперь вверх по строкам матрицы и выполняя расчеты, последовательно получим x₃=0.7971, x₂=-0.1015 и x₁=0.3333. Сравнивая полученное этим методом решение с решением, полученным методом Крамера, нетрудно убедиться в их совпадении.

Метод Гаусса-Жордана. Этот Гаусса-Жордана решения СЛАУ во многом похож на метод Гаусса. Основным отличием является то, что используя эквивалентные преобразования расширенная матрица системы уравнений приводится не к треугольному виду, а к диагональному виду, на главной диагонали которой находятся единицы, а вне нее (кроме последнего n+1 столбца) - нули. После окончания такого преобразования - последний столбец расширенной матрицы будет содержать решение исходной СЛАУ. Обратный ход (как в методе Гаусса) для окончательных расчетов значений компонент решения - не нужен.

Приведение матрицы к диагональному виду проводится, в основном, также как и в методе Гаусса. Если в строке i коэффициент при x_i (i=1, 2, … , n) по абсолютной величине мал, то производится поиск строки j, в которой коэффициент при x_i будет наибольшим по абсолютной величине эта (j-я) строка прибавляется поэлементно к i-й строке. Затем все элементы i-й строки делятся на значение элемента a_ii. Но, в отличие от метода Гаусса, после этого идет вычитание из каждой строки с номером j строки с номером i, умноженной на a_ji, но условие j > i заменено на другое В методе Гаусса-Жордана идет вычитание из каждой строки с номером j, причем j # i, строки с номером i, умноженной на a_ji. Т.е. производится обнуление коэффициентов как ниже, так и выше главной диагонали.

Достаточно подробный алгоритм решения СЛАУ методом Гаусса–Жордана приведен на рис. 2.2.

Пример 3. Найти методом Гаусса-Жордана решение той же СЛАУ, которую мы уже решали методами Крамера и Гаусса.

Полностью аналогично методу Гаусса составим расширенную матрицу системы. Затем переставим местами первую и третью строки этой матрицы (так как в ее первом столбце находится наибольший по абсолютной величине элемент), а затем разделим все элементы этой новой первой строки на значение 3. Дальше проведем вычитание из каждой строки матрицы (кроме первой) элементов первой строки,

Ввод значения размерности N и N строк коэффициентов расширенной матрицы.

f := 0 ; i :=1;

f – флаг вырожденности матрицы

нет

да

Поиск строки k, в которой  a_ki  = max  a_ji  для j  i.

Ко всем элементам строки i прибавить соответ. элементы строки k

да

Деление всех элементов строки i на значение элемента a _ii

f :=1

k := 1

да

да

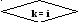
От всех элементов строки k вычесть соответствующие элементы строки i, умноженные на значение a_ki

Прямой ход.

k := k + 1

i := i + 1

да

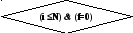
нет

да

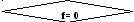
x_i := a _{i N+1} (i=1, 2, … , N)