Вычислим ее норму. Получим

Очевидно, что итерационный процесс для такой матрицы сходящимся не будет. Необходимо найти иной способ преобразования заданной системы уравнений.

Переставим в исходной системе уравнений отдельные ее уравнения так, чтобы третья строка стала первой, первая - второй, вторая - третьей. Тогда, преобразуя ее тем же способом, получим

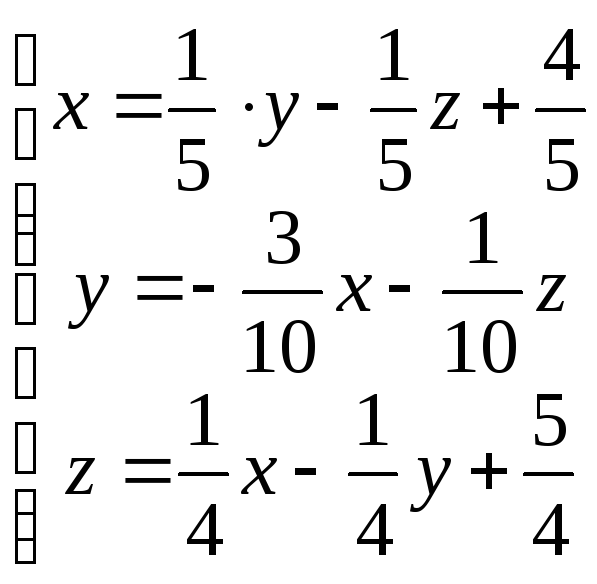
Матрица D такой системы будет

D =.

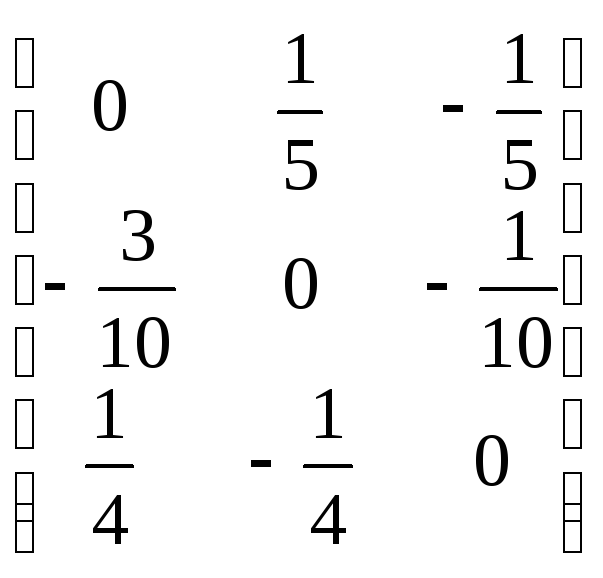Вычислим ее норму. Получим

Так как норма матрицы d оказалась меньшей единицы, преобразованная таким образом система пригодна для решения методом простой итерации.

Пример 3. Преобразуем систему уравнений

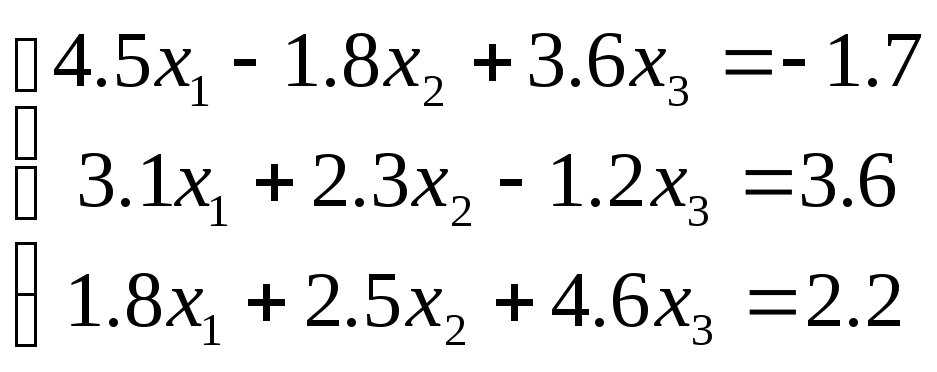
к виду, который позволил бы использовать при ее решении метод простой итерации.

Поступим сначала аналогично примеру 1. Получим

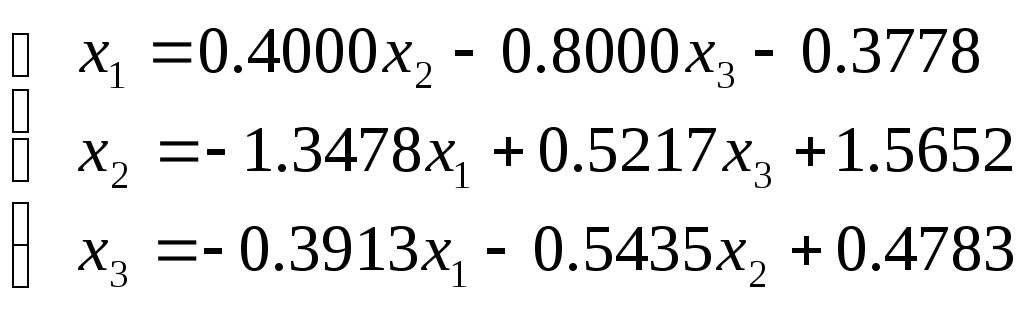
Матрица D такой системы будет

D =.

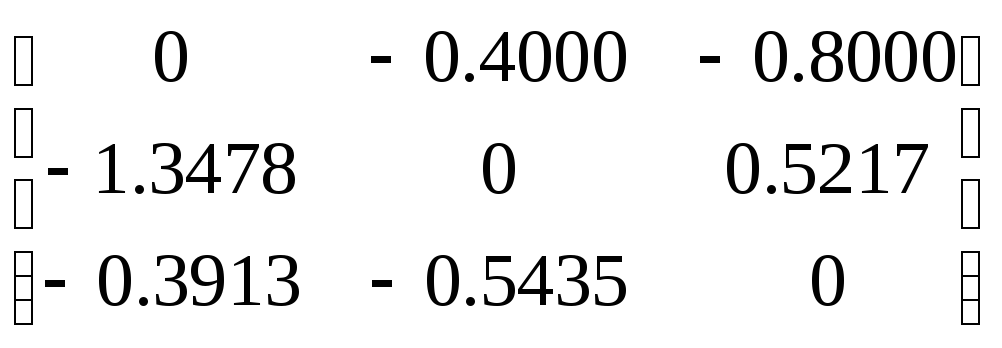Вычислим ее норму. Получим

Очевидно, что итерационный процесс для такой матрицы сходящимся не будет.

Для преобразования исходной матрицы к виду, удобному для применения метода простой итерации поступим следующим образом. Сначала образуем “промежуточную” систему уравнений, в которой

• первое уравнение является суммой первого и второго уравнений исходной системы

• второе уравнение - суммой удвоенного третьего уравнения со вторым за вычетом первого

• третье уравнение - разность третьего и второго уравнений исходной системы.

В результате получим эквивалентную исходной “промежуточную” систему уравнений

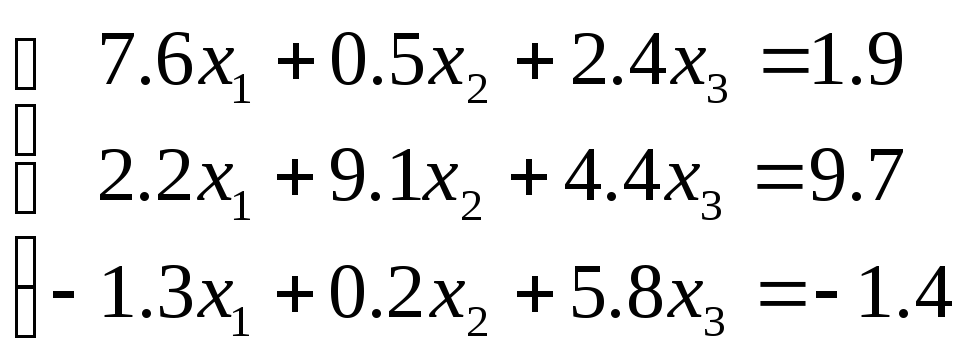
Из нее несложно получить еще одну систему “промежуточную” систему

,

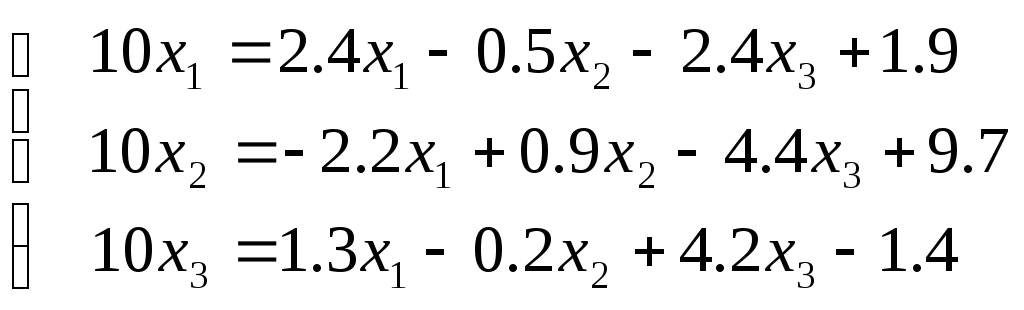а из нее преобразованную

.

Матрица D такой системы будет

D =.

Вычислим ее норму. Получим

Итерационный процесс для такой матрицы будет сходящимся.

Метод Якоби предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде

(3.7)

Из такой записи системы образована итерационная формула метода Якоби

. (3.8)

Условием сходимости итерационного процесса метода Якоби является так называемое условие доминирования диагонали. Аналитически это условие записывается в виде

. (3.9)

Следует отметить, что если в заданной системе уравнений условие сходимости метода Якоби (т.е. условие доминирования диагонали) не выполняется, во многих случаях можно путем эквивалентных преобразований исходной СЛАУ привести ее решение к решению эквивалентной СЛАУ, в которой это условие выполняется.

Пример 4. Преобразуем систему уравнений

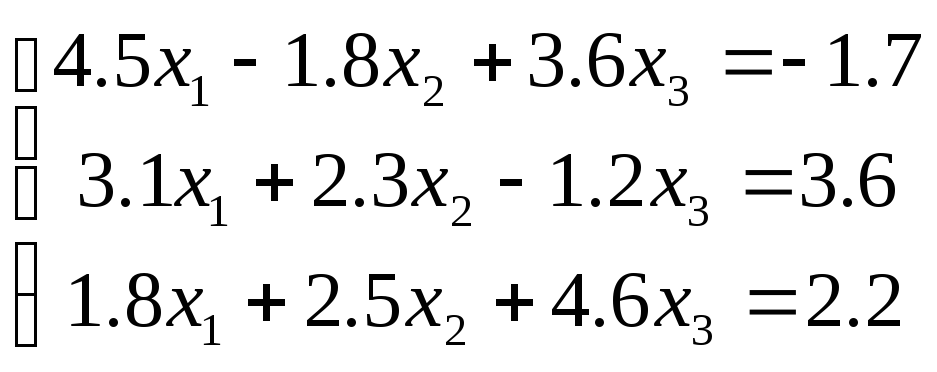
к виду, который позволил бы использовать при ее решении метод Якоби.

Эту систему мы уже рассматривали в примере 3, поэтому перейдем от нее к полученной там “промежуточной” системе уравнений. Легко установить, что у нее условие доминирования диагонали выполняется, поэтому преобразуем ее к виду, необходимому для применения метода Якоби. Получим

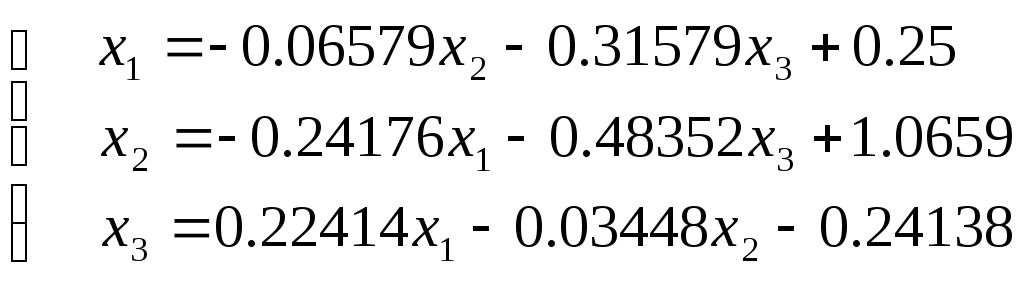
Из нее получаем формулу для выполнения вычислений по методу Якоби для заданной СЛАУ

Взяв за начальное, т.е. нулевое, приближение вектор свободных членов выполним все необходимые вычисления. Результаты сведем в таблицу

M					
0	0.25000	1.06590	-0.24138		-
1	0.256100	1.122172	-0.222097		0.056272
2	0.246318	1.111374	-0.222760		0.010798
3	0.247200	1.114018	-0.224493		0.002644
4	0.247601	1.114684	-0.224384		0.000666
5	0.247523	1.114534	-0.224317		0.000150
6	0.247512	1.114521	-0.224329	0.000013

Довольно высокая точность полученного решения достигнута за шесть итераций.

Метод Гаусса-Зейделя является усовершенствованием метода Якоби и также предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде аналогичном методу Якоби, но несколько отличном от него

.

Здесь важно помнить, что если в знаке суммирования верхний индекс меньше нижнего, то никакого суммирования не производится.

Идея метода Гаусса-Зейделя заключается в том, что авторы метода усмотрели возможность ускорить процесс вычислений по отношению к методу Якоби за счет того, что в процессе очередной итерации найдя новое значение x₁ можно сразу же использовать это новое значение в этой же итерации для вычисления остальных переменных. Аналогично этому, дальше, найдя новое значение x₂ можно его также сразу использовать в этой же итерации и т.д.

Исходя из этого, формула итераций для метода Гаусса-Зейделя имеет следующий вид

. (3.10)

Достаточным условием сходимости итерационного процесса метода Гаусса-Зейделя является все то же условие доминирования диагонали (3.9). Скорость сходимости этого метода несколько выше, чем в метода Якоби.

Пример 5. Решим методом Гаусса-Зейделя систему уравнений

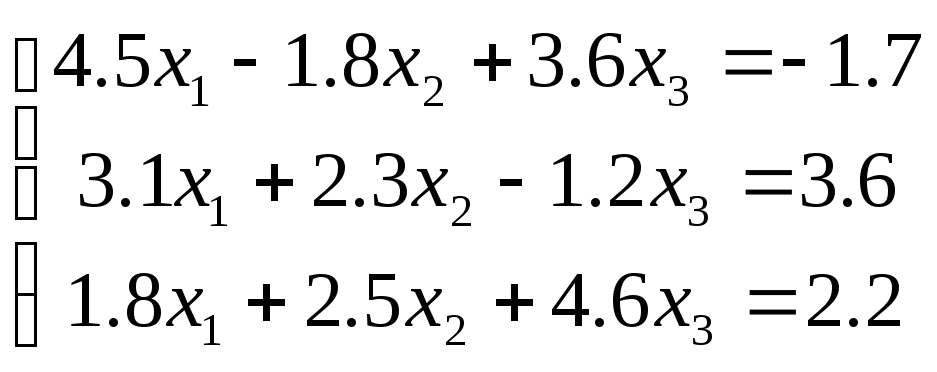
Эту систему мы уже рассматривали в примерах 3 и 4, поэтому сразу перейдем от нее к преобразованой системе уравнений (см. пример 4), в которой условие доминирования диагонали выполняется. Из нее получаем формулу для выполнения вычислений по методу Гаусса-Зейделя

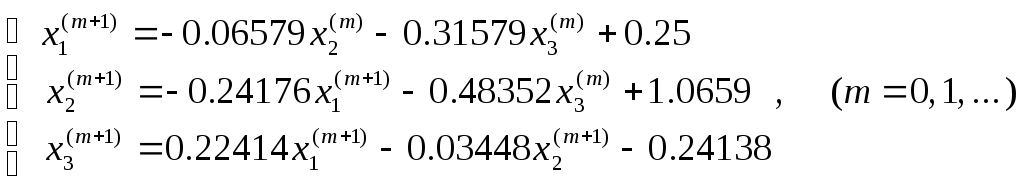
Взяв за начальное (т.е. нулевое) приближение вектор свободных членов, выполним все необходимые вычисления. Результаты сведем в таблицу

M				
0	0.25000	1.06590	-0.24138	-
1	0.25610	1.12070	-0.22262	0.0548
2	0.24657	1.11393	-0.22452	0.00953
3	0.24762	1.11460	-0.22431	0.00105
4	0.24751	1.11452	-0.22433	0.00011
5	0.24750	1.11453	-0.22433	0.00001

Довольно высокая точность полученного решения достигнута за пять итераций.