Тема 3. Обращение квадратных матриц,

Матрица B является обратной матрицей к заданной исходной матрице A размером в n строк и n столбцов, если произведение матриц AB=BA=E. Здесь E - единичная матрица размерности nn. Такая матрица обозначается через A^-1.

Имеются много различных методов обращения квадратных матриц. Рассмотрим некоторые из них.

Метод Гаусса-Жордана основан на сведении процесса обращения заданной квадратной матрицы A размерности nn к решению n систем линейных алгебраических уравнений относительно неихвестных элементов обратной матрицы.

Обозначим через a_ij(i, j = 1, 2, … , n) элементы исходной (обращаемой) матрицы A, через x_ij(i, j = 1, 2, … , n) элементы искомой (обратной) матрицы A^-1, а через _ij(i, j = 1, 2, … , n) элементы единичной матрицы E (_ij=1 при i=j и _ij=0 при ij). Тогда матричное уравнение AA^-1=E, где неизвестной является матрица A^-1, в координатной записи будет иметь следующий вид

Если взять конкретное значение j, то получится система линейных алгебраических уравнений, решением которой является j-й столбец обратной матрицы. Таким образом, решив n систем линейных уравнений с одинаковыми матрицами, мы найдем все n столбцов обратной матрицы. Если производить решение каждой такой системы методом Гаусса-Жордана, то приведение исходной матрицы к единичной матрице можно производить только один раз, а пересчет векторов правых частей (их количество равно n) можно производить параллельно с приведением исходной матрицы.

Этот процесс удобно производить с оспользованием расширенной матрицы размером в n строк и 2n столбцов. В ней первые n столбцов должны занимать столбцы исходной матрицы, а последние n столбцов - единичная матрица. Эта единичная матрица представляет собой набор из n векторов правых частей решаемых систем уравнений.

Пример 1 . Методом Гаусса-Жордана обратить матрицу

A = .

Составим расширенную матрицу, состоящую из исходной и единичной матриц. Получим

A* = .

Шаг 1. Заменяя вторую строку на разность второй и первой строк, а третью - на сумму третьей и первой строк, получим

Шаг 2. Разделим вторую строку на значение коэффициента a₂₂, равного 2. Затем заменим третью строку на сумму третьей строки и только-что полученной второй, а четвертую - на разность ее с умноженной на 2 второй строкой. Получим

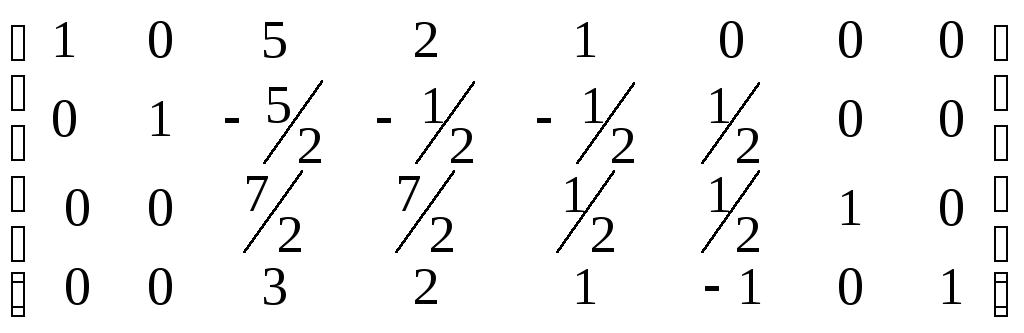Шаг 3. Разделим третью строку на значение коэффициента a₃₃, равного 7/2. Затем заменим первую строку на разность ее и только-что полученной третьей строки, умноженной на 5. Вторую строку заменим на разность ее и только-что полученной третьей строки, умноженной на -5/2. Четвертую - на разность ее с умноженной на 3 третьей строкой. Получим

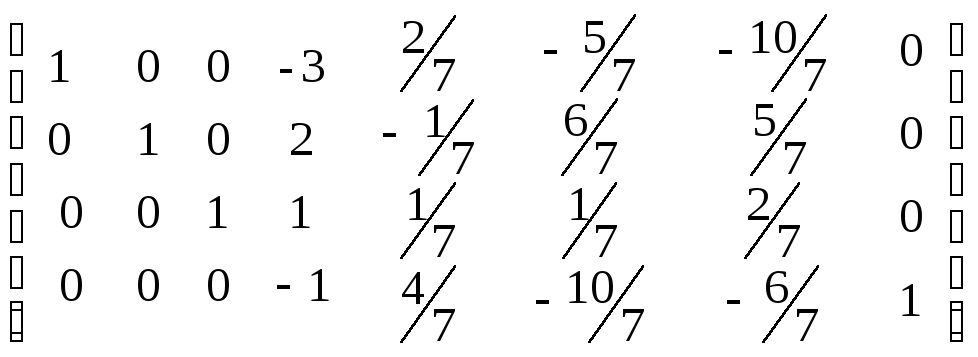Шаг 4. Разделим четвертую строку на значение коэффициента a₄₄, равного -1. Затем заменим первую строку на разность ее и только-что полученной четвертой строки, умноженной на -3. Вторую строку заменим на разность ее и только-что полученной четвертой строки, умноженной на 2. Третью - на разность ее с четвертой строкой. Получим

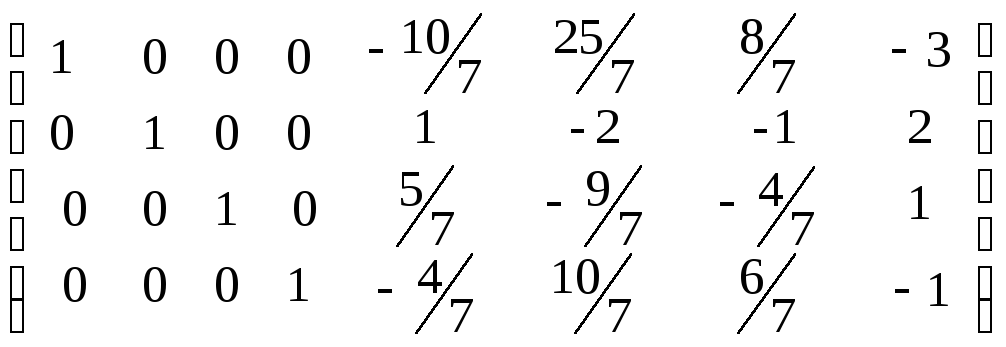Шаг 5. Так как первые четыре столбца только-что полученной матрицы представляют собой единичную матрицу, то согласно методу обращения матриц Гаусса-Жордана последние четыре столбца ее представляют собой обратную матрицу к заданной. Следовательно, имеем

A^-1 = .

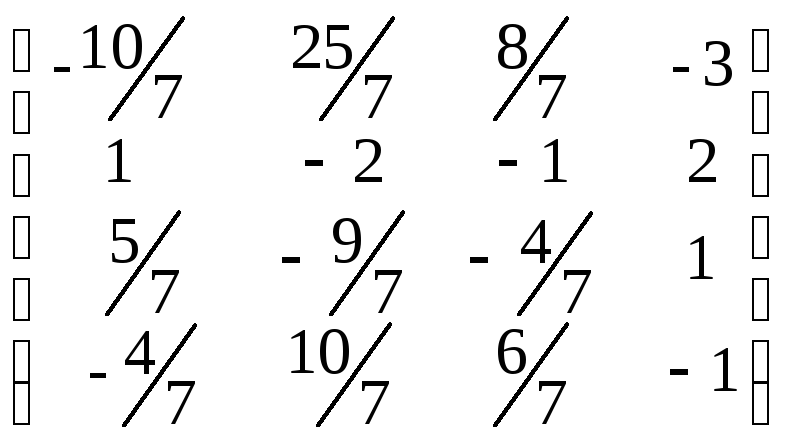Шаг 6. Проверка результата. Так как полученная обратная матрица совпадает с обращаемой матрицей, полученной в примере 1, то проверка выполненная там достаточна для подтверждения правильности полученного результата.