Система не имеет решений

Вывод значений корней

Р

Обратный ход.

ис. 2.2. Алгоритм решения систем линейных алгебраических уравнений методом Гаусса-Жордана.

умноженных на коэффициент в первом столбце этой строки. Получим то же, что и в методе Гаусса

A* = .

Дальше переставим местами вторую и третью строки этой матрицы, разделим вторую строку переставленной матрицы на 2.3333 и (уже в отличие от метода Гаусса) обнулим коэффициенты во втором столбце первой, третьей и четвертой строк матрицы. Получим

A* = .

После этого разделим все элементы третьей строки на -1.8572, а затем вычитая из каждой строки (кроме третьей) вновь полученную третью строку, умноженную на коэффициент, стоящий на пересечении этой строки и третьего столбца. Получим

A* = .

После этого разделим все элементы четвертой строки на -5.3076, а затем вычитая из каждой строки (кроме четвертой) вновь полученную четвертую строку, умноженную на коэффициент, стоящий на пересечении этой строки и четвертого столбца. Получим окончательно

A* = .

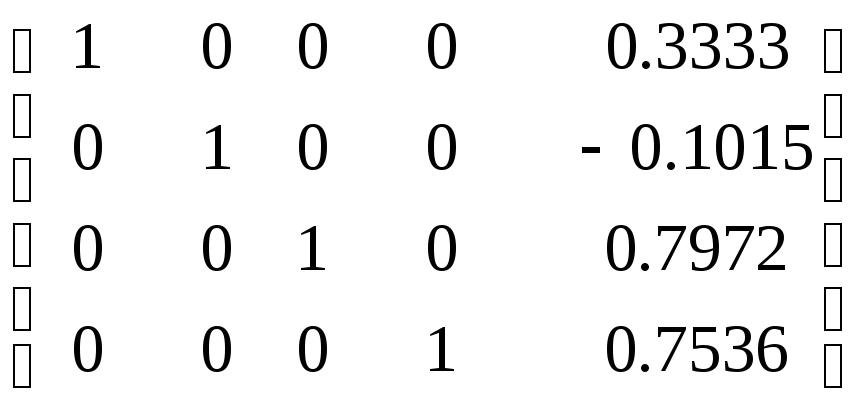В результате всего получим диагональную матрицу с единичными элементами по диагональ и вектором решения в последнем столбце. Решение совпадает с полученным ранее другими методами.

Матричный метод предполагает нахождение матрицы, обратной к матрице A (она обозначается через A^-1), а затем нахождение вектора решения по формуле

x = A^-1B. (2.5)

Все вычисления удобно производить в Excel c использованием функций МОБР и МУМНОЖ.

Пример 4. Решим тот пример матричным методом. Имеем

A=, B=.

Найдем обратную матрицу к матрице A. Получим

A^-1 = .

Теперь по формуле (2.5) получим вектор с решением нашей СЛАУ

x = .

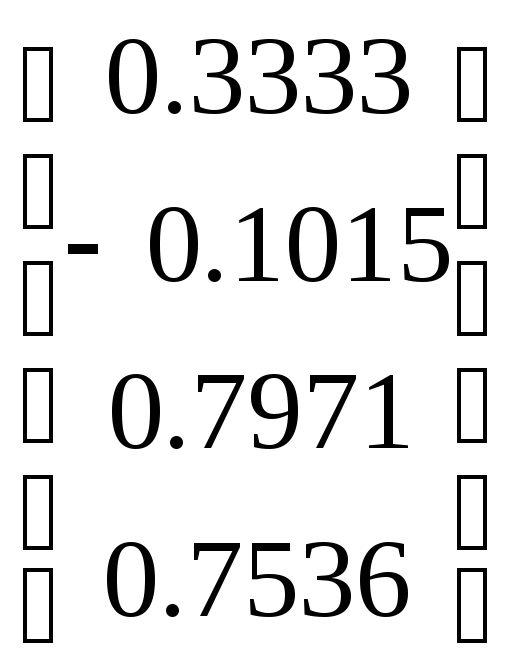Тема 2. Решение систем линейных алгебраических уравнений итерационными методами.

Итерационные методы решения СЛАУ (их второе название - методы последовательного приближения к решению) не дают точного решения СЛАУ, а дают только приближение к решению, причем каждое следующее приближение получается из предыдущего и является более точным, чем предыдущее (при условии, что обеспечена сходимость итераций). Начальное (или, так называемое, нулевое) приближение выбирается вблизи предполагаемого решения или произвольно (в качестве его можно взять вектор правой части системы). Точное решение находится как предел таких приближений при стремлении их количества к бесконечности. Как правило, за конечное число шагов (т.е. итераций) этот предел не достигается. Поэтому, на практике, вводится понятие точности решения, а именно задается некоторое положительное и достаточно малое число  и процесс вычислений (итераций) проводят до тех пор, пока не будет выполнено соотношение

.

Здесь - приближение к решению, полученное после итерации номер n, а - точное решение СЛАУ (которое заранее неизвестно). Число итераций n=n(), необходимое для достижения заданной точности для конкретных методов можно получить из теоретических рассмотрений. Качество различных итерационных методов можно сравнить по необходимому числу итераций для достижения одной и той же точности.

Для исследования итерационных методов на сходимость необходимо уметь вычислять нормы матриц. Норма матрицы - это некая числовая величина, характеризующая величину элементов матрицы по абсолютной величине. В высшей математике имеется несколько различных видов норм матриц, которые, как правило, являются эквивалентными. В нашем курсе мы будем пользоваться только одной из них. А именно, под нормой матрицы мы будем понимать максимальную величину среди сумм абсолютных величин элементов отдельных строк матрицы. Так, для матрицы A под ее нормой будем понимать величину

. (3.1)

Наиболее широкое применение для решения СЛАУ получили три итерационных метода

• метод простой итерации

• метод Якоби

• метод Гуасса-Зейделя.

Метод простой итерации предполагает переход от записи СЛАУ в исходном виде (2.1) к записи ее в виде

(3.2)

или, что тоже, в матричном виде,

x = Dx + B, (3.3)

где :

D - матрица коэффициентов системы размерности nn

x - вектор неизвестных, состоящий из n компонент

B - вектор правых частей системы, состоящий из n компонент.

Формула простой итерации будет иметь вид

(3.4)

где m - номер итерации, а - значение x_j на m-ом шаге итерации. Тогда, если процесс итераций сходится, с увеличением количества итераций будет наблюдаться

Доказано, что процесс итераций сходится, если норма матрицы D будет меньше единицы.

Если за начальное (нулевое) приближение взять вектор свободных членов, т.е. x⁽⁰⁾ = B, то величина погрешности имеет вид

(3.5)

здесь под x^* понимается точное решение системы. Следовательно,

если , то по заданной точности  можно заранее расчитать необходимое количество итераций. А именно, из соотношения

после небольших преобразований получим

. (3.6)

При выполнении такого количества итераций гарантировано будет обеспечена заданная точность нахождения решения системы. Эта теоретическая оценка необходимого количества шагов итерации несколько завышена, на практике необходимая точность может быть достигнута и за меньшее количество итераций.

Поиск решений заданной СЛАУ методом простой итерации удобно производить с занесением полученных результатов в таблицу следующего вида :

M	x1	x2	…	xn
0
1
…

Следует особо отметить, что в решении СЛАУ этим методом наиболее сложным является выполнение преобразования системы из вида (2.1) к виду (2.7). Эти преобразования должны быть эквивалентными, т.е. не меняющими решения исходной системы, и обеспечивающие величину нормы матрицы D (после выполнения их) меньшей единицы. Единого рецепта для выполнения таких преобразований не существует. Здесь в каждом конкретном случае необходимо проявлять творчество. Рассмотрим примеры, в которых будут приведены некоторые способы преобразования системы к необходимому виду.

Пример 1. Найдем решение системы линейных алгебраических уравнений методом простой итерации (с точностью =0.001)

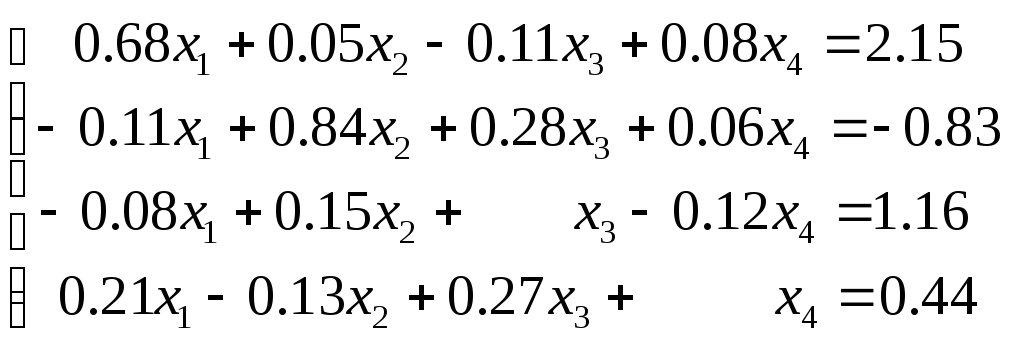
Эта система приводится к необходимому виду простейшим способом. Перенесем все слагаемые из левой части в правую, а затем к обоим частям каждого уравнения прибавим по x_i (i=1, 2, 3, 4). Получим преобразованную систему следующего вида

.

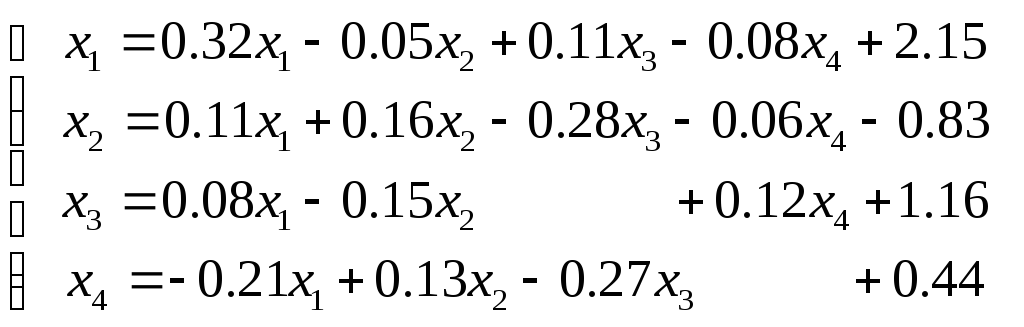Матрица D и вектор B в этом случае будут следующими

D = , B = .
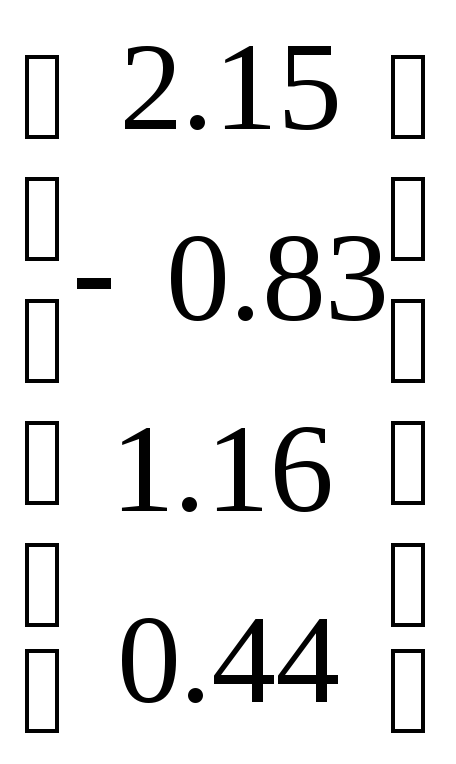