
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
-
Производная неявной функции
Пусть функция
![]() задана неявно,
т.е уравнением
задана неявно,
т.е уравнением
![]() ,
неразрешенным относительно
,
неразрешенным относительно
![]() .
Чтобы найти производную от
.
Чтобы найти производную от
![]() по
по
![]() ,
нужно продифференцировать это уравнение,
учитывая, что
,
нужно продифференцировать это уравнение,
учитывая, что
![]() является
функцией от
является
функцией от
![]() .
Затем из полученного выражения выразить
.
Затем из полученного выражения выразить
![]() .
.
Пример 1. Найти
производную
![]() функции
функции
![]() .
.
Найдем производные
по
![]() от каждой части уравнения.
от каждой части уравнения.
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Пример 2. Найти
производную второго порядка
![]() от функции, заданной неявно:
от функции, заданной неявно:
![]()
1) Найдем
![]() :
:
![]() ,
,
![]() .
.
2) Найдем
![]() :
:
![]() ,
заменим
,
заменим
![]()
 .
.
11.6. Производная функции, заданной параметрически
Будем говорить,
что переменная
![]() как функция аргумента
как функция аргумента
![]() задана параметрически,
если обе переменные
задана параметрически,
если обе переменные
![]() и
и
![]() заданы как функции некоторой третьей
переменной
заданы как функции некоторой третьей
переменной
![]() :
:
![]() ,
где
,
где
![]() – параметр
(дополнительная переменная).
– параметр
(дополнительная переменная).
Предположим, что
существуют
![]() и
и
![]() ,
а функция
,
а функция
![]() имеет обратную функцию
имеет обратную функцию
![]() .
Тогда
.
Тогда
![]() .
.
В этом случае,
параметрически заданную функцию можно
рассматривать как сложную функцию
![]() .
.
Тогда
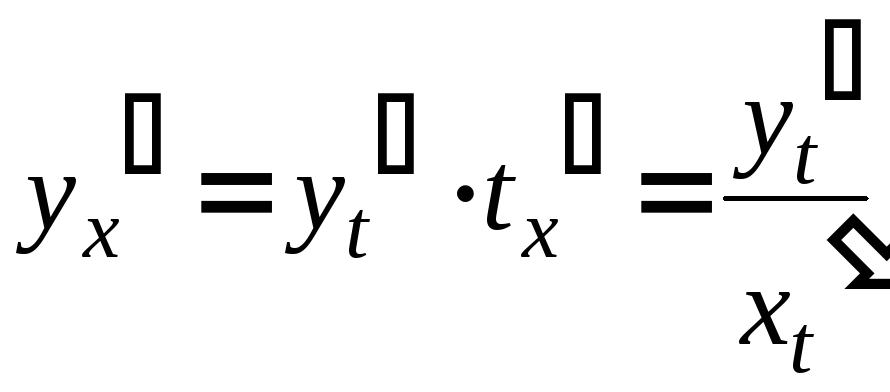
![]()
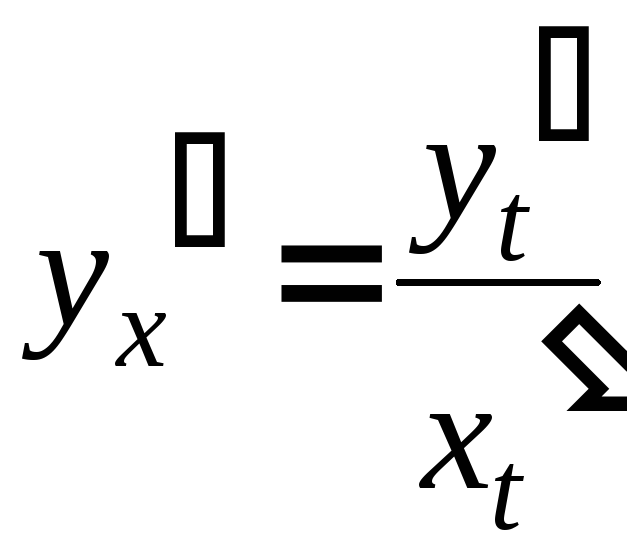 .
.
Производная второго порядка находится по формуле :
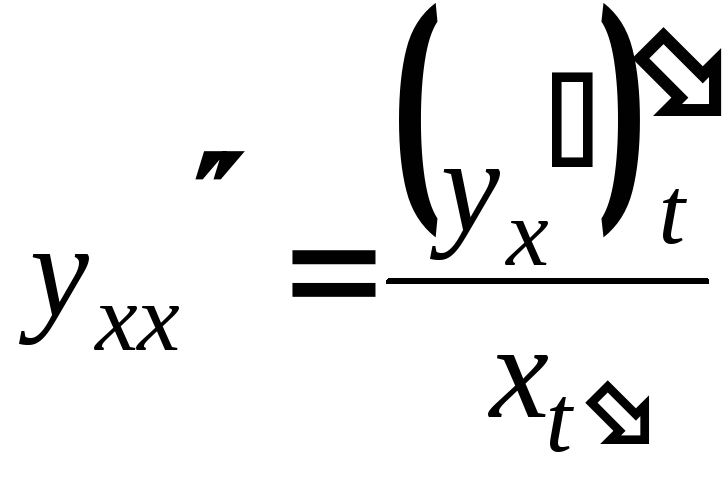 или
или
 .
.
Пример 1.
Функция задана параметрически:![]() .
.
Найти производную
второго порядка по
![]() .
.
![]()
![]()
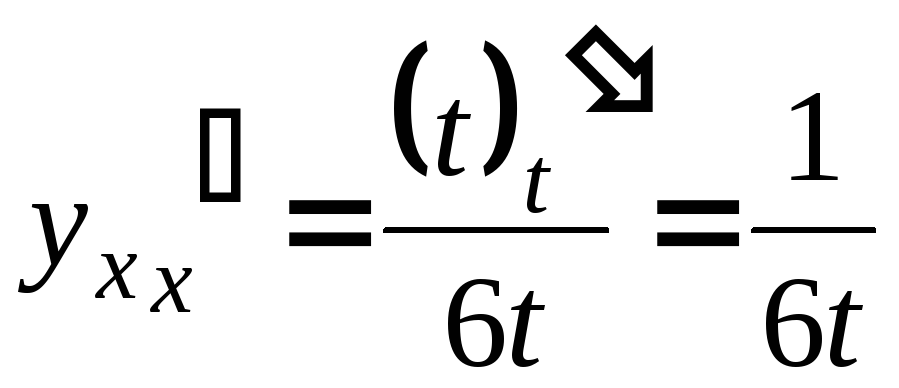 .
.
Пример 2.
Функция задана параметрически:
![]() .
.
Найти производную
второго порядка по
![]() .
.
![]()
![]()
![]() .
.
§ 12. Дифференциал функции
Пусть функция
![]() имеет отличную от нуля производную
имеет отличную от нуля производную
![]() .
.
Тогда по теореме
о связи функции, ее предела и б.м.ф.
можно записать
![]() ,
где
,
где
![]() при
при
![]() .
.
![]()
![]() – это сумма двух
б.м.ф. при
– это сумма двух
б.м.ф. при
![]() .
При этом первое слагаемое б.м.ф
одного
порядка с
.
При этом первое слагаемое б.м.ф
одного
порядка с
![]()
![]() ,
а второе слагаемое б.м.ф
более
высокого порядка, чем
,
а второе слагаемое б.м.ф
более
высокого порядка, чем
![]()
![]() .
.
Поэтому первое
слагаемое
![]() является главной
частью приращения функции
является главной
частью приращения функции
![]() и называется дифференциалом
первого порядка функции
и называется дифференциалом
первого порядка функции
![]() в точке
в точке
![]() .
.
Обозначают
дифференциал так:
![]() или
или
![]() .
.
Дифференциал
равен произведению производной функции
![]() и приращения аргумента
и приращения аргумента
![]() .
Найдем дифференциал аргумента
.
Найдем дифференциал аргумента
![]()
![]()
![]() .
.
Следовательно,
![]() .
.
Геометрический смысл дифференциала первого порядка.
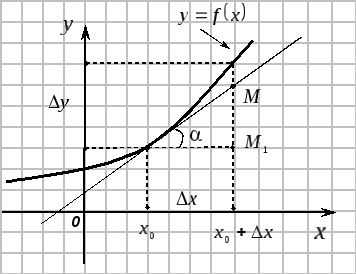
![]()
Следовательно,
дифференциал первого порядка функции
![]() в точке
в точке
![]() – это
приращение
ординаты касательной, проведенной к
графику функции в точке
– это
приращение
ординаты касательной, проведенной к
графику функции в точке
![]() .
.
Если
![]() ,
то
,
то
![]() .
Последнее равенство можно использовать
для приближенного вычисления значения
.
Последнее равенство можно использовать
для приближенного вычисления значения
![]() .
.
Пример 1.
Вычислить
![]() .
.
Пусть
![]() .
.
Тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§ 13. Основные теоремы дифференциального исчисления
1. Теорема Ферма. (Ферма Пьер (1601–1665гг.) – французский математик).
Пусть функция
![]() определена
на интервале
определена
на интервале
![]() ;
в некоторой точке
;
в некоторой точке
![]() этого интервала она принимает наибольшее
или наименьшее значение.
этого интервала она принимает наибольшее
или наименьшее значение.
Тогда, если в точке
![]() существует
конечная производная, то она равна нулю,
т.е.
существует
конечная производная, то она равна нулю,
т.е.
![]() .
.
Геометрический смысл теоремы Ферма.
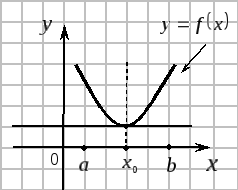
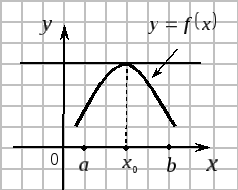
![]()
![]()
![]()
![]() касательная
параллельна оси
касательная
параллельна оси
![]() .
.
2. Теорема Ролля. (Ролль Мишель (1652–1719гг.) – французский математик)
Пусть функция
![]() определена
на
определена
на
![]() ,
,
причем: 1)
![]() непрерывна
на
непрерывна
на
![]() ;
;
2)
![]() дифференцируема на
дифференцируема на
![]() ;
;
3)
![]() .
.
Тогда существует
точка
![]() ,
в которой
,
в которой
![]() .
.
