10.3. Физический смысл производной
Пусть
функция
описывает закон движения материальной
точки
по прямой линии, в том смысле, что значение
- это путь, пройденный точкой за время
.
Тогда
– это мгновенная
скорость точки
в момент времени
.
§ 11. Правила дифференцирования функций и производные элементарных функций
-
Правила дифференцирования
Пусть
функции
и
дифференцируемы.
Тогда:
;
;
;
Производную сложной функции находим по формуле:
.
11.2. Производные элементарных функций
Используя
определение производной, можно показать,
что 
– производная
постоянной функции;
– производная
степенной функции.
Выведем производные остальных элементарных функций.
Производные тригонометрических функций.
1.
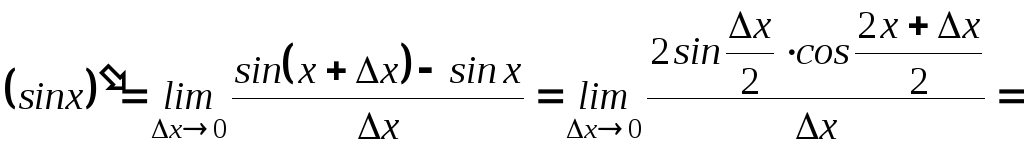
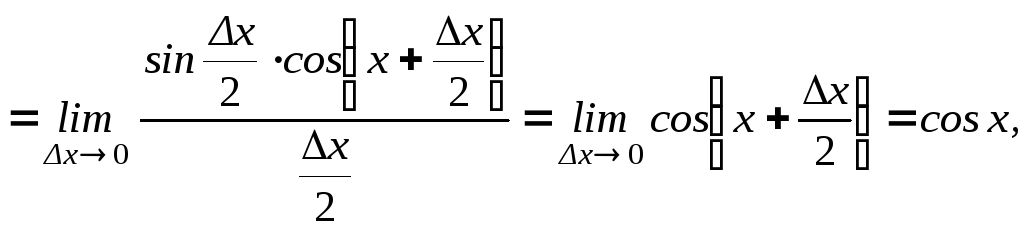
( применили первый замечательный предел)
т.е.
.
2.
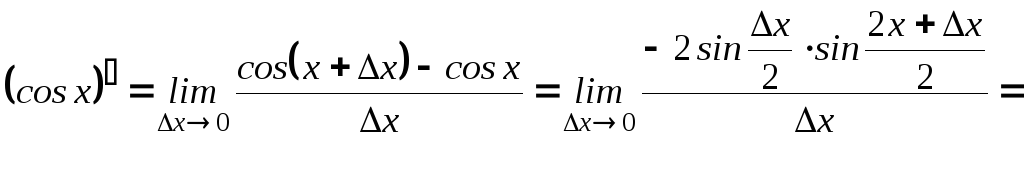
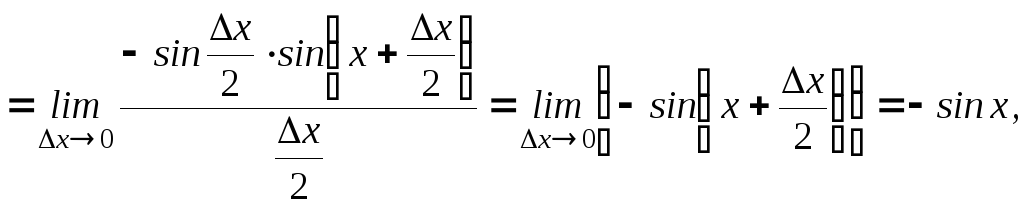
( применили первый замечательный предел)
т.е
.
3.
т.е.
.
4.
т.е.
.
Производная логарифмической функции.
(умножили и разделили
на
)
(применили второй замечательный предел
)
т.е.
.
Частный случай:
.
Производная обратной функции. Производная показательной функции.
1.
Теорема.
Если
в точке
имеет
,
то обратная ей функция
также в точке
имеет
,
причем
.
2.
Показательная функция
,
обратная ей функция
.
,
т.е.
.
Частный случай:
.
Производные обратных тригонометрических функций.
1.
Пусть функция
,
где
,
тогда
– обратная ей
функция,
.
Знак « + » перед
корнем, так как функция
неотрицательна на отрезке
.
Следовательно,
.
Аналогично получаем:
.
2.
Пусть функция
,
где
,
тогда
- обратная ей функция,
.
Следовательно,
.
Аналогично получаем:
.
11.3. Логарифмическое дифференцирование
В некоторых случаях для нахождения производной сначала можно функцию прологарифмировать, а затем от полученного выражения вычислить производную.
Такая операция называется логарифмическим дифференцированием.
Существуют функции, производные от которых находят лишь с помощью логарифмического дифференцирования.
К таким функциям
относится показательно-степенная
функция
.
Прологарифмируем
выражение
.
Найдем производную
от обеих частей полученного равенства,
учитывая, что
является функцией от
.
Тогда
или
.
Пример 1.
Найти производную функции
.
Прологарифмируем
выражение:
Тогда
или
.
Пример 2.
Найти производную функции
.
Прологарифмируем выражение:
Тогда
или
.
11.4. Производные высших порядков
Производная
от функции
есть также функция от
и называется производной первого
порядка.
Производная от
производной первого порядка называется
производной второго
порядка и
обозначается
.
Производная от
производной (
)-го
порядка
называется производной
-го
порядка и
так далее. Начиная с четвертого порядка,
производные обозначаются:
или
,
или
и так далее.
Например:
,
,
,
,
.
Физический смысл производной второго порядка.
Если функция
описывет закон движения материальной
точки по прямой линии, то
– ускорение
точки в момент времени
.