
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
6.4. Два замечательных предела
Первый замечательный
предел.
![]()
Докажем это равенство.
Возьмем круг радиуса 1.
Пусть угол
![]() радиан.
радиан.
Тогда дуга
![]() радиан,
радиан,
![]() ,
,
![]()
П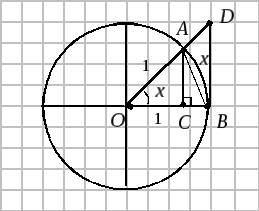 лощадь
треугольника
лощадь
треугольника
![]() .
.
Площадь сектора
![]() .
.
Площадь треугольника
![]() .
.
![]()
![]()
![]()
![]()
![]() или
или
![]() .
.
![]() ,
,
![]()
![]()
![]() ( по теореме о
промежуточной функции )
( по теореме о
промежуточной функции )
Следствия:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
П
 ример
1.
ример
1.
![]() .
.
П
 ример
2.
ример
2.
 .
.
Второй замечательный предел.
Две формулировки второго замечательного предела:
![]()
![]()
Раскрывает
неопределенность
![]() .
.
Пример.
![]()
Замечание.
Второй замечательный предел можно
применять и при
![]() .
.
§ 7. Бесконечно большие и бесконечно малые функции
(б.б.ф. и б.м.ф.)
7.1. Бесконечно большие функции и их свойства
Определение.
Функция
![]() называется бесконечно
большой функцией
при
называется бесконечно
большой функцией
при
![]() ,
если для любого числа
,
если для любого числа
![]() существует число
существует число
![]() такое,
что для всех
такое,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
В этом случае записывают
.
В этом случае записывают
![]() и говорят функция
имеет бесконечный предел в точке
и говорят функция
имеет бесконечный предел в точке
![]() .
.
Краткая запись определения:
![]()
![]()
Аналогично
определяются б.
б. ф. при
![]() .
.
Например:
1)
![]() при
при
![]() является бесконечно большой функцией.
является бесконечно большой функцией.
2)
![]() при
при
![]() является бесконечно большой функцией.
является бесконечно большой функцией.
Свойства б. б. ф.
-
Сумма конечного числа б. б. ф. есть б. б. ф.
-
Произведение б. б. ф. на число есть б. б. ф.
-
Произведение двух б. б. ф. есть б. б. ф.
7.2. Бесконечно малые функции и их свойства
Определение.
Функция
![]() называется бесконечно
малой функцией
при
называется бесконечно
малой функцией
при
![]() ,
если
,
если
![]() .
.
Аналогично
определяются бесконечно малые функции
при
![]() .
.
Бесконечно малые
функции иначе называют бесконечно
малыми величинами, или бесконечно
малыми, и обозначают греческими буквами
![]() .
.
Примеры б.
м. ф. функций:
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
![]() при
при
![]() .
.
Свойства б. м. ф.
-
Алгебраическая сумма конечного числа б. м. ф. есть б. м. ф.
-
Произведение ограниченной функции на б. м. ф. есть б. м. ф.
-
Произведение б. м. ф. на число есть б. м. ф.
-
Произведение двух б. м. ф. есть б. м. ф.
-
Частное от деления б. м. ф. на функцию, имеющую отличный от нуля предел , есть б. м. ф.
-
Частное от деления функции, имеющей отличный от нуля предел, на б. м. ф. есть б. б. ф.
-
Частное от деления функции, имеющей отличный от нуля предел, на б. б. ф. есть б. м. ф.
-
Если функция
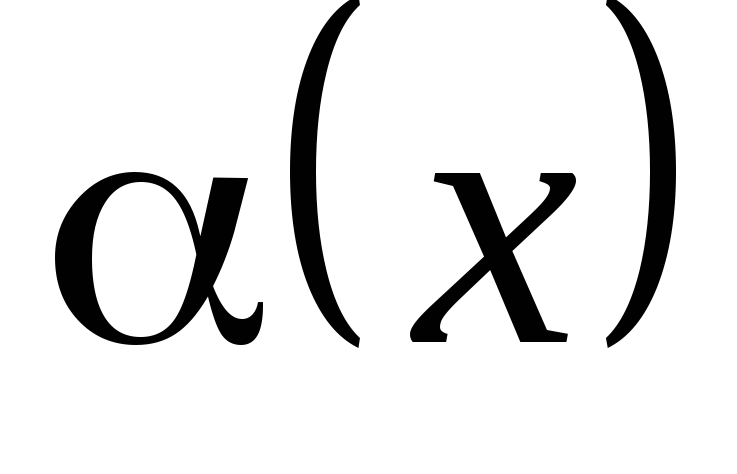 является б.
м. ф. и не
равна нулю, то функция
является б.
м. ф. и не
равна нулю, то функция
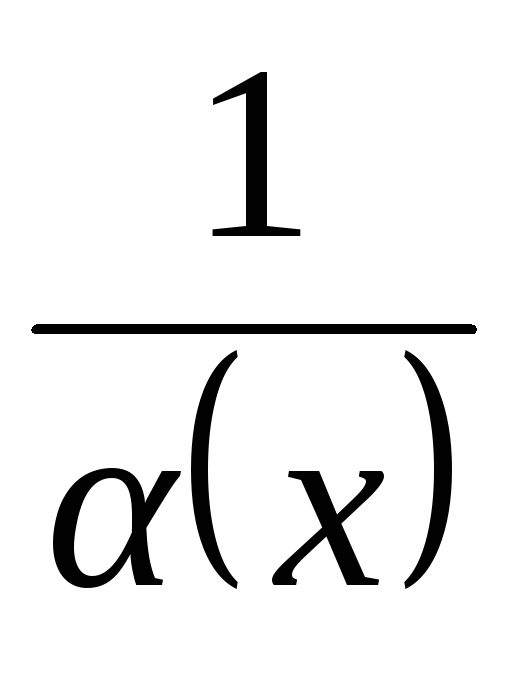 есть б. б. ф.
и наоборот, если функция
есть б. б. ф.
и наоборот, если функция
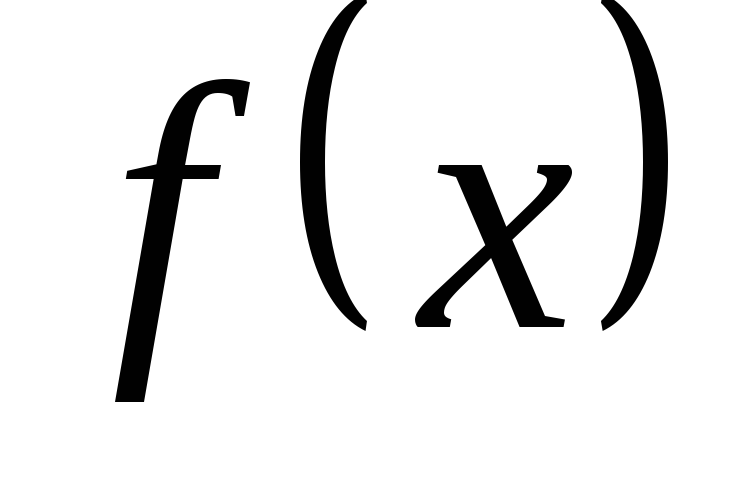 является б.
б. ф., то
функция
является б.
б. ф., то
функция
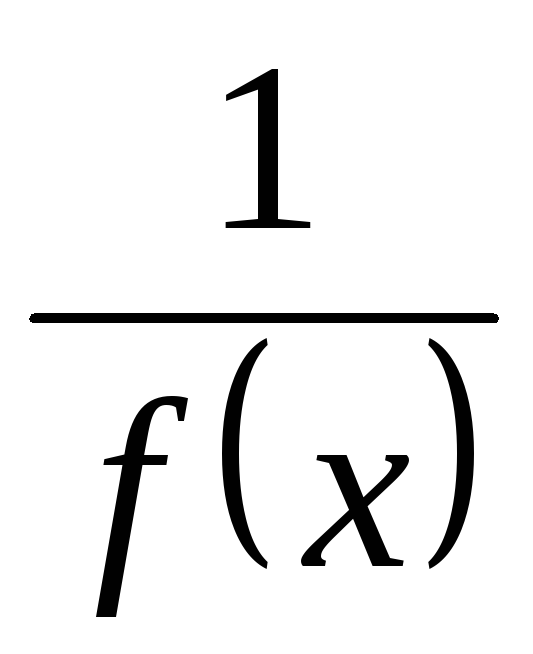 есть б. м. ф.
есть б. м. ф.
Примеры вычисления пределов с помощью свойств б. б. ф. и б. м. ф.
|
1.
|
2.
|
|
3.
|
4.
|
7.3. Связь между функцией, ее пределом и б. М. Ф.
Теорема.
Если
![]() , то
, то
![]() ,
,
где
![]() - это б. м. ф.
при
- это б. м. ф.
при
![]() .
.
Доказательство.
![]()
![]()
![]() ,
,
т.е.
![]()
![]()
![]() .
.
Следовательно
![]() это б. м. ф.
при
это б. м. ф.
при
![]() ,
которую обозначим через
,
которую обозначим через
![]() .
Таким образом,
.
Таким образом,
![]()
![]()
![]() ¢.
¢.
Теорема.
(обратная)
Если
![]() ,
то
,
то
![]()
Доказательство.
Так как
![]() есть б. м. ф.
при
есть б. м. ф.
при
![]() , то
, то
![]()
![]()
![]() .
.
![]() ¢
¢
