
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
§ 4. Классификация функций
4.1. Обратная функция
Пусть
![]() функция от
функция от
![]() с областью значений
с областью значений
![]() .
Пусть, кроме того, каждому значению
.
Пусть, кроме того, каждому значению
![]() соответствует только
одно значение
соответствует только
одно значение
![]() .
Тогда на множестве
.
Тогда на множестве
![]() определена функция
определена функция
![]() с областью значений
с областью значений
![]() ,
обладающая свойством
,
обладающая свойством
![]() для любого
для любого
![]() из множества
из множества
![]() .
.
Функция
![]() называется обратной к функции
называется обратной к функции![]() .
Если
.
Если
![]() – обратная функция к
– обратная функция к
![]() ,
то функция
,
то функция
![]() – обратная функция к
– обратная функция к
![]() .
Про функции
.
Про функции
![]() и
и
![]() говорят, что они являются взаимно
обратными.
говорят, что они являются взаимно
обратными.
Ч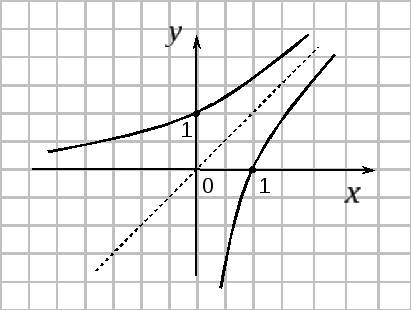 тобы
найти функцию
тобы
найти функцию![]() ,
обратную к функции
,
обратную к функции
![]() ,
достаточно решить уравнение
,
достаточно решить уравнение
![]() относительно
относительно
![]() .
Традиционно независимую переменную
обозначают
.
Традиционно независимую переменную
обозначают
![]() ,
а зависимую
,
а зависимую
![]() .
.
Например, функции
![]() и
и
![]() взаимно обратные. Графики их симметричны
относительно биссектрисы I
и III
координатных углов.
взаимно обратные. Графики их симметричны
относительно биссектрисы I
и III
координатных углов.
Из определения
обратной функции следует, что для любой
строго монотонной функции существует
обратная. При
этом если
![]() возрастает, то и
возрастает, то и
![]() также возрастает.
также возрастает.
Например, функция
![]() на
на
![]() строго возрастает.
строго возрастает.
На этом промежутке
существует обратная ей функция
![]() ,
которая также возрастает.
,
которая также возрастает.
4.2. Сложная функция
Пусть функция
![]() определена
на множестве
определена
на множестве
![]() ,
а функция
,
а функция
![]() определена на множестве
определена на множестве
![]() ,
причем
,
причем
![]() соответствующее значение
соответствующее значение
![]() .
Тогда функция
.
Тогда функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
называется сложной
функцией (
или суперпозицией
заданных функций или функцией
от функции)
с аргументом
,
называется сложной
функцией (
или суперпозицией
заданных функций или функцией
от функции)
с аргументом
![]() .
.
Например,
![]() – сложная функция, аргумент
– сложная функция, аргумент
![]() .
.
4.3. Основные элементарные функции и их графики
Основными элементарными функциями называют следующие функции.
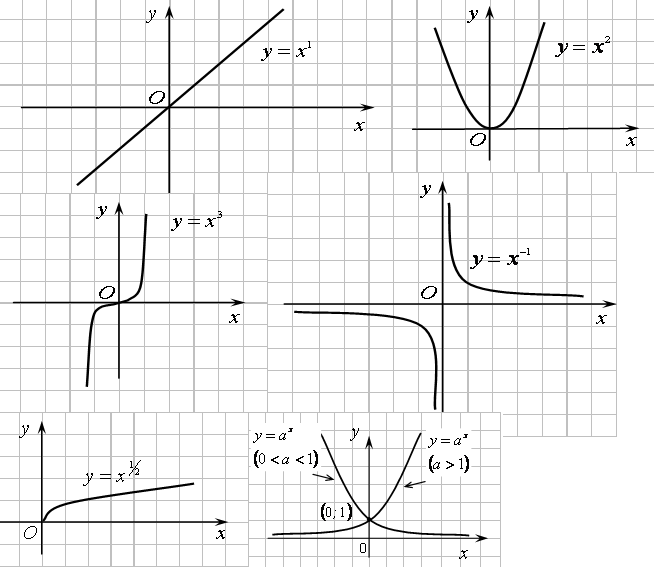
1.
Степенная функция
![]() ,
,
![]() .
.
Примеры графиков степенных функций, соответствующих различным показателям степени, показаны на рисунках.
2. Показательная
функция
![]() ,
,
![]() ,
,
![]() .
.
На рисунке показаны графики функций, соответствующие различным основаниям.
3 .
Логарифмическая
функция
.
Логарифмическая
функция
![]() ,
,
![]() ,
,
![]() .
.
Графики логарифмических функций, соответствующие различным основаниям логарифма, показаны на рисунке.
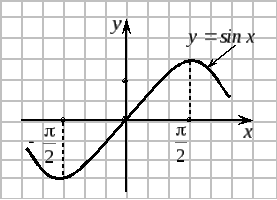
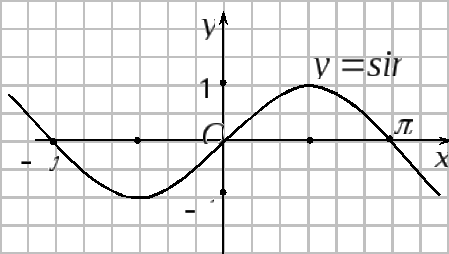
4. Тригонометрические
функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
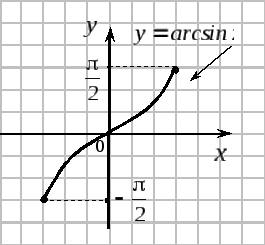
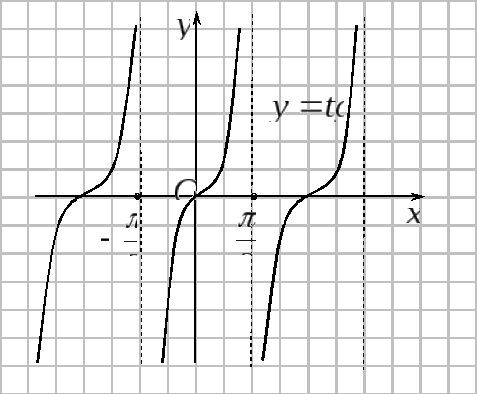
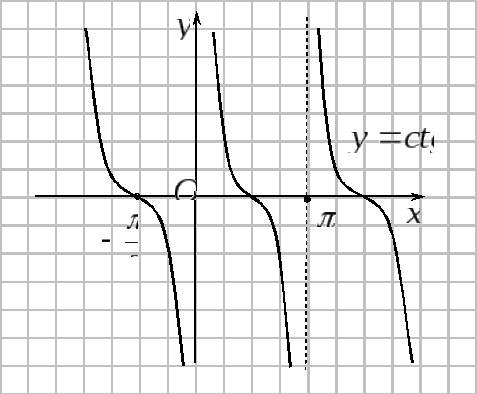
Графики тригонометрических функций показаны на рисунках.

5. Обратные
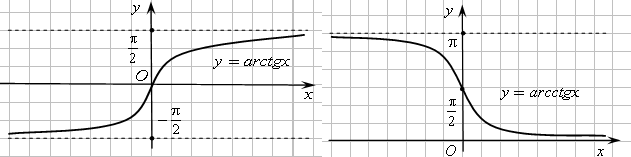
тригонометрические
функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Графики обратных тригонометрических функций показаны на рисунках:

Все функции, получаемые из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными функциями.
Например:
функции
![]() ,
,
![]() ,
,
![]() – элементарные; функция
– элементарные; функция
 не является элементарной.
не является элементарной.
§ 5. Числовые последовательности
Бесконечной
числовой последовательностью называется
числовая функция натурального аргумента,
т.е. функция, определенная на множестве
![]() .
Она записывается
.
Она записывается
![]() или сокращенно
или сокращенно
![]() ,
где
,
где
![]() – элементы
или члены числовой последовательности;
– элементы
или члены числовой последовательности;
![]() – номер члена
последовательности;
– номер члена
последовательности;
![]() – общий или
– общий или
![]() -ый
член последовательности.
-ый
член последовательности.
Последовательность
считается заданной, если известна
формула для
![]() .
.
Например,
![]()
Последовательность
![]() называется ограниченной,
если существует такое число
называется ограниченной,
если существует такое число
![]() ,
что для любого
,
что для любого
![]() выполняется неравенство
выполняется неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Например,
![]() – ограничена, так как
– ограничена, так как
![]() ;
;
![]() – неограничена.
– неограничена.
Можно заметить,
что члены последовательности
![]() при
при
![]() ,
неограниченно приближаются к
,
неограниченно приближаются к
![]() .
.
В этом случае говорят, что число 1 называется пределом данной последовательности.
Определение.
Число
![]() называется пределом
последовательности
называется пределом
последовательности
![]() при
при
![]() ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа
![]() найдется такое натуральное число
найдется такое натуральное число
![]() (зависящее от
(зависящее от
![]() ),
что для всех членов последовательности
с номерами
),
что для всех членов последовательности
с номерами
![]() выполняется неравенство
выполняется неравенство
![]() .
При этом пишут:
.
При этом пишут:
![]() и говорят, что последовательность
и говорят, что последовательность
![]() сходится к
числу
сходится к
числу
![]() .
.
Определение можно записать с помощью логических символов:
![]()
Геометрический смысл предела последовательности.
Н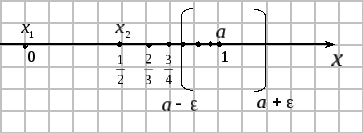 еравенство
еравенство
![]() равносильно неравенству
равносильно неравенству
![]() ,
которое показывает, что
,
которое показывает, что
![]() принадлежит
принадлежит
![]() –
окрестности точки
–
окрестности точки
![]() .
.
Геометрически
определение предела последовательности
можно сформулировать так:
число
![]() называется пределом последовательности
называется пределом последовательности
![]() ,
если для любой
,
если для любой
![]() – окрестности точки
– окрестности точки
![]() найдется такое число
найдется такое число
![]() ,
что все значения
,
что все значения
![]() ,
для которых
,
для которых
![]() ,
попадут в
,
попадут в
![]() – окрестность точки
– окрестность точки
![]() .
.
Из рисунка видно,
что в
![]() – окрестности точки
– окрестности точки
![]() находится бесконечное число членов
последовательности, а вне ее - конечное
число.
находится бесконечное число членов
последовательности, а вне ее - конечное
число.
Отсюда следует, что сходящаяся последовательность имеет только один предел.
Не всякая
последовательность имеет предел.
Последовательность, не имеющая предела,
называется расходящейся
(обозначается
![]() ).
).
Сформулируем признак существования предела последовательности.
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.
Например:
1) Последовательность
![]() – монотонно убывает и ограничена,
следовательно,
– монотонно убывает и ограничена,
следовательно,
![]() .
.
2) Последовательность
![]() – монотонно возрастает и ограничена,
следовательно,
– монотонно возрастает и ограничена,
следовательно,
![]() .
.
Можно показать,
что число
![]() ,
является основанием натурального
логарифма
,
является основанием натурального
логарифма
![]() .
.
