
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
§ 2. Понятие функции
Одним из основных понятий математики является понятие функции. Оно связано с установлением зависимости (связи) между элементами двух множеств.
Определение.
Если каждому элементу
![]() соответствует единственный элемент
соответствует единственный элемент
![]() ,
то говорят, что на множестве
,
то говорят, что на множестве
![]() задана функция
задана функция
![]() (
(![]() -
знак функции).
-
знак функции).
Переменную
![]() называют аргументом
или независимой
переменной, а
переменную
называют аргументом
или независимой
переменной, а
переменную
![]() –
зависимой переменной от х; множество
–
зависимой переменной от х; множество
![]() –
областью определения функции
–
областью определения функции
![]() ,
а множество
,
а множество
![]() –
множеством значений функции
–
множеством значений функции
![]() ,
,
![]() – закон соответствия.
– закон соответствия.
![]() – множество значений аргумента, при
которых формула
– множество значений аргумента, при
которых формула
![]() имеет смысл.
имеет смысл.
Кроме буквы
![]() для обозначения функций используют и
другие буквы греческого и латинского
алфавитов:
для обозначения функций используют и
другие буквы греческого и латинского
алфавитов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() и так далее.
и так далее.
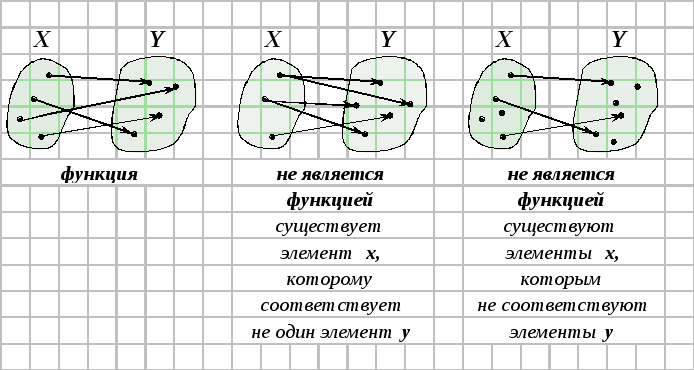
Примеры.
1)
![]() ,
,
![]() .
.
2)
![]() ,
,
![]() .
.
3)
![]() или
или
![]() ,
,
![]() .
.
4)
![]() ,
,
![]() .
.
Если элементами
множеств
![]() и
и
![]() являются действительные числа, то
функция называется числовой.
являются действительные числа, то
функция называется числовой.
Частное значение
функции при
![]() обозначают так:
обозначают так:![]() .
.
Например,
![]()
![]()
![]()
График
функции
![]() – это множество точек плоскости с
координатами
– это множество точек плоскости с
координатами
![]() ,
где
,
где
![]() ,
для каждой из которых
,
для каждой из которых
![]() является значением аргумента, а
является значением аргумента, а
![]() является соответствующим значением
функции.
является соответствующим значением
функции.
Способы задания функции.
1. Аналитический: функция задается с помощью одной или нескольких формул, или уравнений.
Если область определения функции не указана, то она совпадает со множеством всех значений аргумента, при которых указанная формула имеет смысл.
2. Графический: задается график.
3. Табличный: с помощью таблицы ряда значений аргумента и соответствующих значений функции, полученных в результате некоторого опыта.
4. Словесный: функция описывается правилом ее составления.
Например, функция
Дирихле
![]() ,
если
,
если
![]()
![]() ,
если
,
если
![]() – иррациональное.
– иррациональное.
§ 3. Основные характеристики функции
1.Функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
область опреления которой симметрична
относительно начала координат, называется:
четной,
если
,
область опреления которой симметрична
относительно начала координат, называется:
четной,
если
![]() выполняются условия
выполняются условия
![]() и
и
![]() ;
нечетной,
если
;
нечетной,
если
![]() выполняются условия
выполняются условия
![]() и
и
![]() .
В противном случае функция
.
В противном случае функция
![]() называется функцией общего
вида.
называется функцией общего
вида.
График четной
функции симметричен относительно оси
![]() ,
график нечетной функции симметричен
относительно начала координат.
,
график нечетной функции симметричен
относительно начала координат.
Например, функция
![]() -
четная, а функция
-
четная, а функция
![]() –функция
общего вида.
–функция
общего вида.
2.
Пусть функция
![]() определена на множестве
определена на множестве
![]() ,
интервал
,
интервал
![]() .
.
Если для любых
![]() и
и
![]() из интервала
из интервала![]() ,
причем
,
причем
![]() ,
выполняется неравенство:
,
выполняется неравенство:
1)
![]() ,
то функция
,
то функция
![]() называется неубывающей
на
называется неубывающей
на
![]() ;
;
2)
![]() ,
то функция
,
то функция
![]() называется невозрастающей
на
называется невозрастающей
на
![]() ;
;
3)
![]() ,
то функция
,
то функция
![]() называется возрастающей
на
называется возрастающей
на
![]() ;
;
4)
![]() ,
то функция
,
то функция
![]() называется убывающей
на
называется убывающей
на
![]() .
.
Во всех рассмотренных случаях функции называются монотонными, а возрастающая и убывающая функции строго монотонными.
Н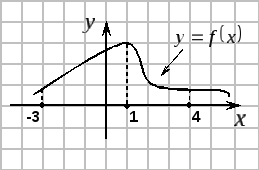 апример,
на рисунке функция
апример,
на рисунке функция
![]() на
на
![]() строго монотонная;
строго монотонная;
на
![]() монотонная.
монотонная.
3.
Функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
называется периодической
на этом
множестве с периодом
,
называется периодической
на этом
множестве с периодом
![]() ,
где
,
где
![]() – положительное число, если выполняются
условия:
– положительное число, если выполняются
условия:
![]() и
и
![]() .
Если
.
Если
![]() – период, то периодом функции также
будут числа
– период, то периодом функции также
будут числа
![]() ,
где
,
где
![]()
Н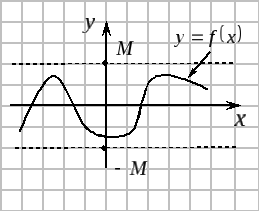 апример,
для функции
апример,
для функции
![]() периодами будут числа
периодами будут числа
![]()
4.
Функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
называется ограниченной
на этом
множестве, если существует такое число
,
называется ограниченной
на этом
множестве, если существует такое число
![]() ,
что для всех
,
что для всех
![]() выполняется неравенство
выполняется неравенство
![]() .
Коротко можно записать так:
.
Коротко можно записать так:
![]() .
.
График ограниченной
функции расположен между прямыми
![]() и
и
![]() .
Например, функция
.
Например, функция
![]() ограничена, так как
ограничена, так как
![]() .
.
